Depending on the requirements, the deployment phase can be as simple as generating a report or as complex as implementing a continuous learning process.

We use the following techniques for deploying a neural network:

• 7.1. Neural network outputs
• 7.2. Output data
• 7.3. Directional outputs
• 7.4. Mathematical expression
• 7.5. Python expression
• 7.6. C++ expression

7.1. Neural network outputs

A neural network produces a set of outputs for each set of inputs applied.

The following table shows the input values and the corresponding output value for estimating a car’s fuel consumption as a function of its attributes.

7.2. Output data

In many cases, the objective is to predict the outputs for many different cases stored in a data file. Each row in the data file contains the input values of the case to be predicted. We create a new file with the model’s outputs arranged in rows.

The next table illustrates this deployment technique. Here, a neural network predicts the probability of conversion for several customers in a marketing campaign as a function of engagement factors.

7.3. Directional outputs

It is useful to see how the outputs vary as a single input function when all the others are fixed. This allows us to perform prescriptions. One can view directional outputs as the cut of the neural network model along some input direction and through some reference points.

The next table shows the reference point for plotting all the directional output charts. In this case, the model estimates the residuary resistance of a sailing yacht as a function of design parameters and sailing conditions.

The next chart shows how the residuary resistance varies with the Froude number (which represents the velocity of the yacht), with all the other inputs being fixed.

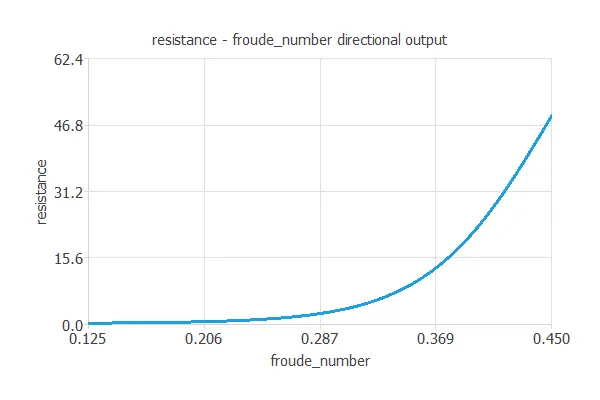
As we can see, the residuary resistance increases exponentially for high values of the Froude number. Therefore, this yacht design does not perform well at high speeds.

7.4. Mathematical expression

Any neural network represents a function of the outputs to the inputs. That function also depends on the parameters. The mathematical expression represented by the neural network can be used to embed it into another software in the so-called production mode.

Next, we list an example of the mathematical model represented by a neural network.

scaled_shear_rate = 2*(shear_rate-50)/(90-50)-1;
scaled_particle_diameter = 2*(particle_diameter-0.72)/(6.596-0.72)-1;
y_1_1 = tanh(-1.06007+(scaled_shear_rate*0.448487)+(scaled_particle_diameter*-0.861393));
y_1_2 = tanh(0.756922+(scaled_shear_rate*2.00716)+(scaled_particle_diameter*0.391539));
y_1_3 = tanh(0.862072+(scaled_shear_rate*-0.726115)+(scaled_particle_diameter*-1.46053));
scaled_particles_adhering = (-1.30536+(y_1_1*-1.0244)+(y_1_2*0.56055)+(y_1_3*-0.565459));
particles_adhering = (0.5*(scaled_particles_adhering+1.0)*(74.75-13.22)+13.22);

We can easily embed the above code into any application that uses the model. We need to adapt the syntax of the mathematical expression to that of the programming language we are using.

7.5. Python expression

We can export the mathematical expression the model represents to different programming languages, such as Python.

The next listing is an example of a neural network in the Python programming language.

def expression(inputs) : 
if type(inputs) != list:
print('Argument must be a list')
return
if len(inputs) != 4:
print('Incorrect number of inputs')
return
temperature=inputs[0]
exhaustt_vacuum=inputs[1]
ambient_pressure=inputs[2]
relative_humidity=inputs[3]
scaled_temperature = (temperature-19.6512)/7.45247
scaled_exhaustt_vacuum = 2*(exhaustt_vacuum-25.36)/(81.56-25.36)-1
scaled_ambient_pressure = (ambient_pressure-1013.26)/5.93878
scaled_relative_humidity = (relative_humidity-73.309)/14.6003
		y_1_1 = tanh (-0.155062+ (scaled_temperature*0.203034)+ (scaled_exhaustt_vacuum*0.731056)+ (scaled_ambient_pressure*-0.191671)+ (scaled_relative_humidity*0.0158643))
		y_1_2 = tanh (-0.29098+ (scaled_temperature*-0.023069)+ (scaled_exhaustt_vacuum*-0.263476)+ (scaled_ambient_pressure*-0.231774)+ (scaled_relative_humidity*0.333626))
		y_1_3 = tanh (0.570558+ (scaled_temperature*0.573079)+ (scaled_exhaustt_vacuum*-0.0279703)+ (scaled_ambient_pressure*0.111165)+ (scaled_relative_humidity*0.00867248))
		scaled_energy_output =  (0.15981+ (y_1_1*-0.383639)+ (y_1_2*-0.126028)+ (y_1_3*-0.745885))
energy_output = (0.5*(scaled_energy_output+1.0)*(495.76-420.26)+420.26)
		return energy_output 

You can easily integrate this code into any Python application that uses the model.

7.6. C++ expression

C++ is one of the most widely used programming languages.

The next code is an example of a neural network in the C programming language.

#include 
using namespace std;
vector scaling_layer(const vector& inputs)
{
vector outputs(5);
outputs[0] = inputs[0]*0.3025558293-1;
outputs[1] = inputs[1]*0.3025558293-1;
outputs[2] = inputs[2]*0.4306863844-0.1386272311;
outputs[3] = inputs[3]*5.421008924e-20-1;
outputs[4] = inputs[4]*5.421008924e-20+1;
return outputs;
}
vector perceptron_layer_0(const vector& inputs)
{
vector combinations(3);
combinations[0] = 0.02009 -0.880635*inputs[0] +0.815813*inputs[1] -0.106329*inputs[2] -0.117222*inputs[3] -0.210783*inputs[4];
combinations[1] = 0.0355442 -0.0121058*inputs[0] +0.0725463*inputs[1] +0.0671187*inputs[2] -0.0893239*inputs[3] +0.205473*inputs[4];
combinations[2] = -0.00834767 +0.0153575*inputs[0] -0.00712658*inputs[1] +0.0125823*inputs[2] -0.0126559*inputs[3] -0.0117719*inputs[4];
vector activations(3);
activations[0] = tanh(combinations[0]);
activations[1] = tanh(combinations[1]);
activations[2] = tanh(combinations[2]);
return activations;
}
vector perceptron_layer_1(const vector& inputs)
{
vector combinations(1);
combinations[0] = -0.044036 +1.01136*inputs[0] -0.244702*inputs[1] +0.00911695*inputs[2];
vector activations(1);
activations[0] = combinations[0];
return activations;
}
vector unscaling_layer(const vector& inputs)
{
vector outputs(1);
outputs[0] = inputs[0]*0.7265999913+0.7265999913;
return outputs;
}
vector bounding_layer(const vector& inputs)
{
vector outputs(1);
outputs[0] = inputs[0];
return outputs;
}
vector neural_network(const vector& inputs)
{
vector outputs;
outputs = scaling_layer(inputs);
outputs = perceptron_layer_0(outputs);
outputs = perceptron_layer_1(outputs);
outputs = unscaling_layer(outputs);
outputs = bounding_layer(outputs);
return outputs;
}
int main(){return 0;}

You can easily embed the above code into any C++ application that uses the model.