Model selection searches for the neural network architecture with the best generalization properties.
That is, the process that minimizes the error on the selected instances of the data set (the selection error).
There are two families of model selection algorithms in machine learning:
1. Neuron selection
Two frequent problems in designing a neural network are called underfitting and overfitting.
The best generalization is achieved using a model with the most appropriate complexity to produce a good data fit.
Underfitting and overfitting
To illustrate underfitting and overfitting, consider the following data set. It consists of data from a sine function to which white noise has been added.
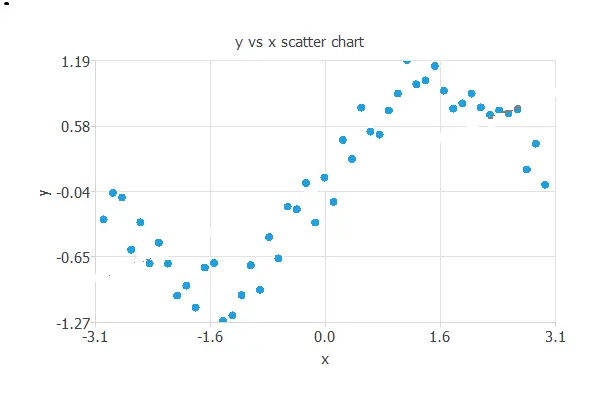
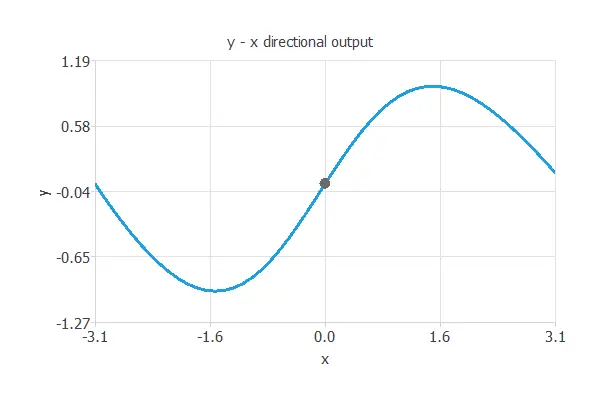
The best generalization is achieved using a model whose complexity is the most appropriate to produce an adequate data fit. In this case, we use a neural network with one input (x), three hidden neurons, and one output (y).
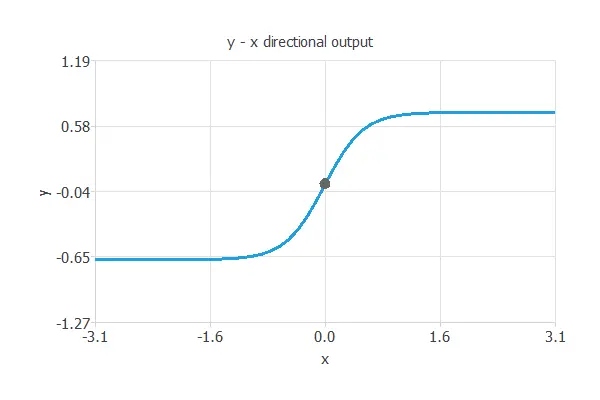
In this way, underfitting is the effect of a selection error increasing due to a too-simple model. Here, we have used one hidden neuron.
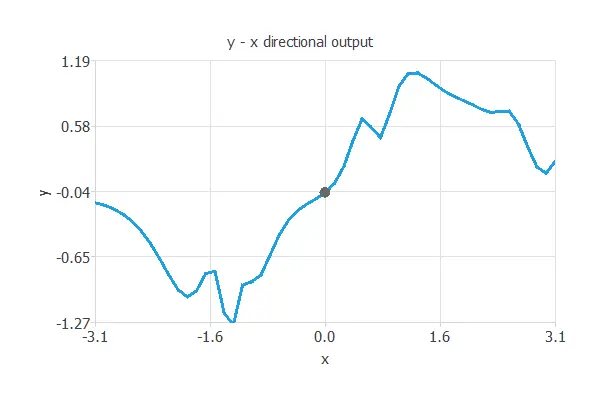
On the contrary, overfitting is the effect of a selection error increasing due to a complex model. In this case, we have used 10 hidden neurons.
The error of a neural network on the training instances of the data set is called the training error. Similarly, the error on the selected instances is called the selection error.
The training error measures the ability of the neural network to fit the data it sees. However, the selection error measures the ability of the neural network to generalize to new data.
The following figure shows the training (blue) and selection (orange) errors as a function of the neural network complexity, represented by the number of hidden neurons.
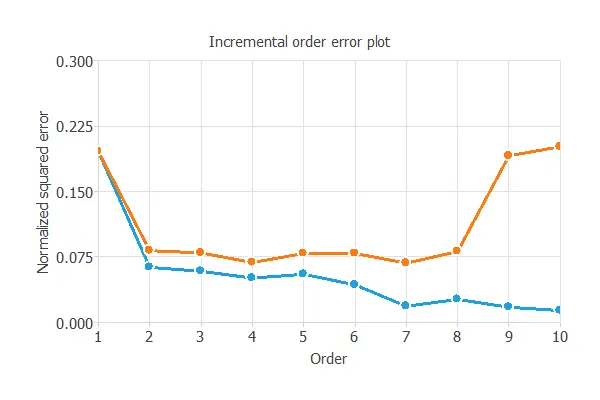
As shown, increasing hidden neurons reduces training error, but both very small and very large networks lead to high selection error.
The first case indicates underfitting, while the second indicates overfitting.
Here, the best generalization occurs with four hidden neurons, where the selection error reaches its minimum.
Neuron selection algorithms find the neural network’s complexity that yields the best generalization properties.
Growing neurons is the most common neuron selection method.
Growing neurons
This algorithm begins with a small network and gradually adds neurons until a stopping criterion is reached.
The algorithm returns the neural network with the optimal number of neurons obtained.
2. Input selection
Which features should you use to create a predictive model? This is a difficult question that may require in-depth knowledge of the problem domain.
Input selection algorithms automatically extract those features in the data set that provide the best generalization capabilities.
They search for the subset of inputs that minimizes the selection error.
The most common input selection algorithms are:
Growing inputs
The growing inputs method calculates the correlation of every input with every output in the data set.
It starts with a neural network that only contains the most correlated input and calculates the selection error for that model.
It continues to add the most correlated variables until the selection error increases.
The algorithm returns the neural network with the optimal subset of inputs found.
Pruning inputs
The pruning inputs method starts with all the inputs in the data set.
It keeps removing those inputs with the smallest correlation with the outputs until the selection error increases.
Genetic algorithm
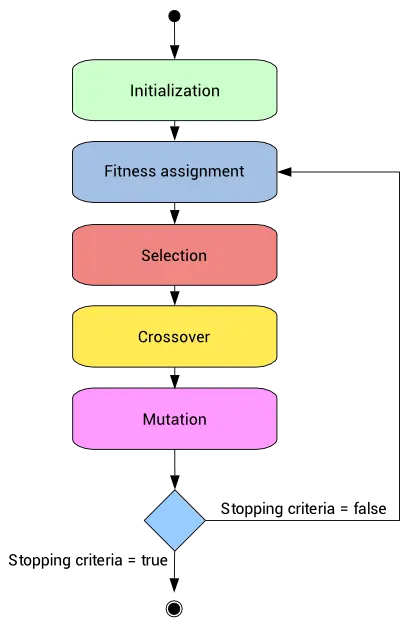
A different class of input selection method is the genetic algorithm.
This is a stochastic method based on natural genetics and biological evolution mechanics.
Genetic algorithms usually include fitness assignment, selection, crossover, and mutation operators.
You can find more information about this topic in the Genetic algorithms for feature selection post on our blog.
Testing Analysis ⇒



