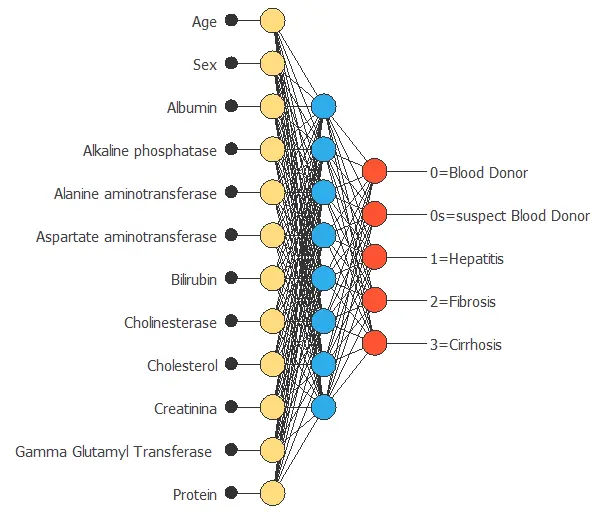
Many typical machine learning applications, from customer targeting to medical diagnosis, arise from complex relationships between features (also called input variables or characteristics). Feature selection or input selection algorithms (such as genetic algorithms) search for the most relevant inputs for a model.
Feature selection techniques help identify and remove unneeded, irrelevant, and redundant features. Indeed, those variables do not contribute to or decrease the accuracy of the predictive model.
Feature selection
Mathematically, we formulate inputs selection as a combinatorial optimization problem.
The objective function is the predictive model’s generalization performance, represented by the error term on the selection instances of a data set.
The design variables are the inclusion (1) or the exclusion (0) of the input variables in the neural network.
A wide selection of features would evaluate 2N different combinations, where N is the number of features.
This process requires lots of computational work, and it becomes impracticable if the number of features is significant.
Therefore, we need intelligent methods to select features in practice.
Genetic algorithms
One of the most advanced algorithms for feature selection is the genetic algorithm.
The genetic algorithm is a stochastic method for function optimization based on natural genetics and biological evolution.
In nature, organisms’ genes tend to evolve over successive generations to better adapt to the environment. The genetic algorithm is a heuristic optimization method inspired by the procedures of natural evolution.
Genetic algorithms operate on a population of individuals to produce better and better approximations.
The algorithm creates a new population every generation by selecting individuals according to their fitness level in the problem domain. These individuals are then recombined together using operators borrowed from natural genetics. The offspring might also undergo mutation.
A state diagram for the feature selection process with the genetic algorithm is depicted next.
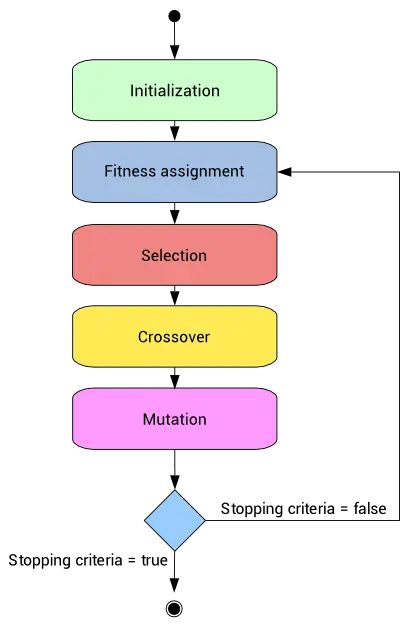
This process leads to the evolution of populations better suited to their environment than the individuals who originated it.
In our case, each individual in the population represents a neural network.
Genes here are binary values, representing the inclusion or not of particular features in the model. The number of genes is the total number of input variables in the data set.
The number of individuals, or population size, must be chosen for each application. The default value for the population size is 10 N, where N is the number of features. This number must be a multiple of 4.
Next, we describe the operators and the corresponding parameters used by the genetic algorithm in detail.
1. Initialization operator
The first step is to create and initialize the individuals in the population. Since the genetic algorithm is a stochastic optimization method, we randomly initialize the genes of all individuals.
To illustrate this operator, consider a predictive model represented by a neural network with 6 possible features. If we generate four individuals, we have four different neural networks with random features.
The next figure illustrates this population.
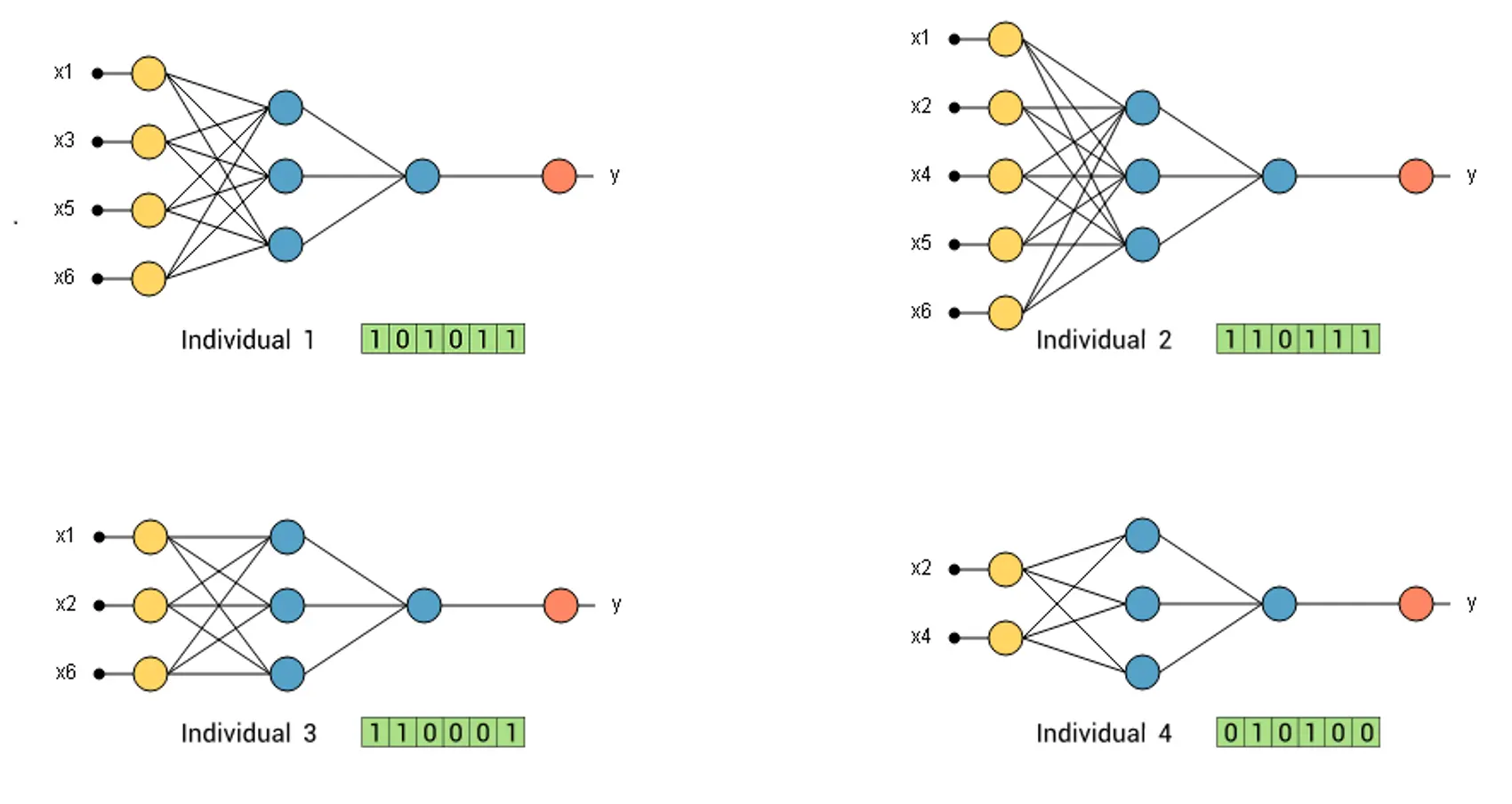
As we can see, each individual is represented by 6 binary genes. Each positive gen means that the corresponding feature is included in the neural network.
Another way to activate columns is according to their correlation with the target variable. In this way, we create a probability
distribution. This distribution is similar to the one created in the selection operator.
This initialization operator causes variables more likely to be the correct ones to be activated at first.
2. Fitness assignment operator
After the initialization, we need to assign a fitness value to each population member.
We train each neural network with the training instances and then evaluate their error with the selection instances.
A significant selection error means low fitness. Individuals with higher fitness or lesser selection error are more likely to be selected for recombination.
The most used method for fitness assignment is known as a rank-based fitness assignment.
With this method, the selection errors of all the individuals are sorted.
Then, the fitness assigned to each individual only depends on its position in the individual’s rank and not on the actual selection error.
The fitness value assigned to each individual with the rank-based method is:
$$\Phi(i) = R(i) \qquad where \quad i = 1,…,N.$$
Here, the parameter R(i) is the rank of individual i. We can then calculate the probability of being selected based on the fitness assigned to each individual. The probability of each individual to be selected it can be calculated with the following expression:
$$\displaystyle P_i=\dfrac{R(i)}{\sum_{j=1}^N j}$$
The following table depicts the selection error, the rank, and the corresponding probability of being selected (fitness) of each individual in our example.
| Selection error | Rank | Probability | |
|---|---|---|---|
| Individual 1 | 0.9 | 1 | 0.1 |
| Individual 2 | 0.6 | 3 | 0.3 |
| Individual 3 | 0.7 | 2 | 0.2 |
| Individual 4 | 0.5 | 4 | 0.4 |
We can plot the above fitness values in a pie chart. Here, the area for each individual in the pie is proportional to its fitness.
The following picture shows the fitness pie.
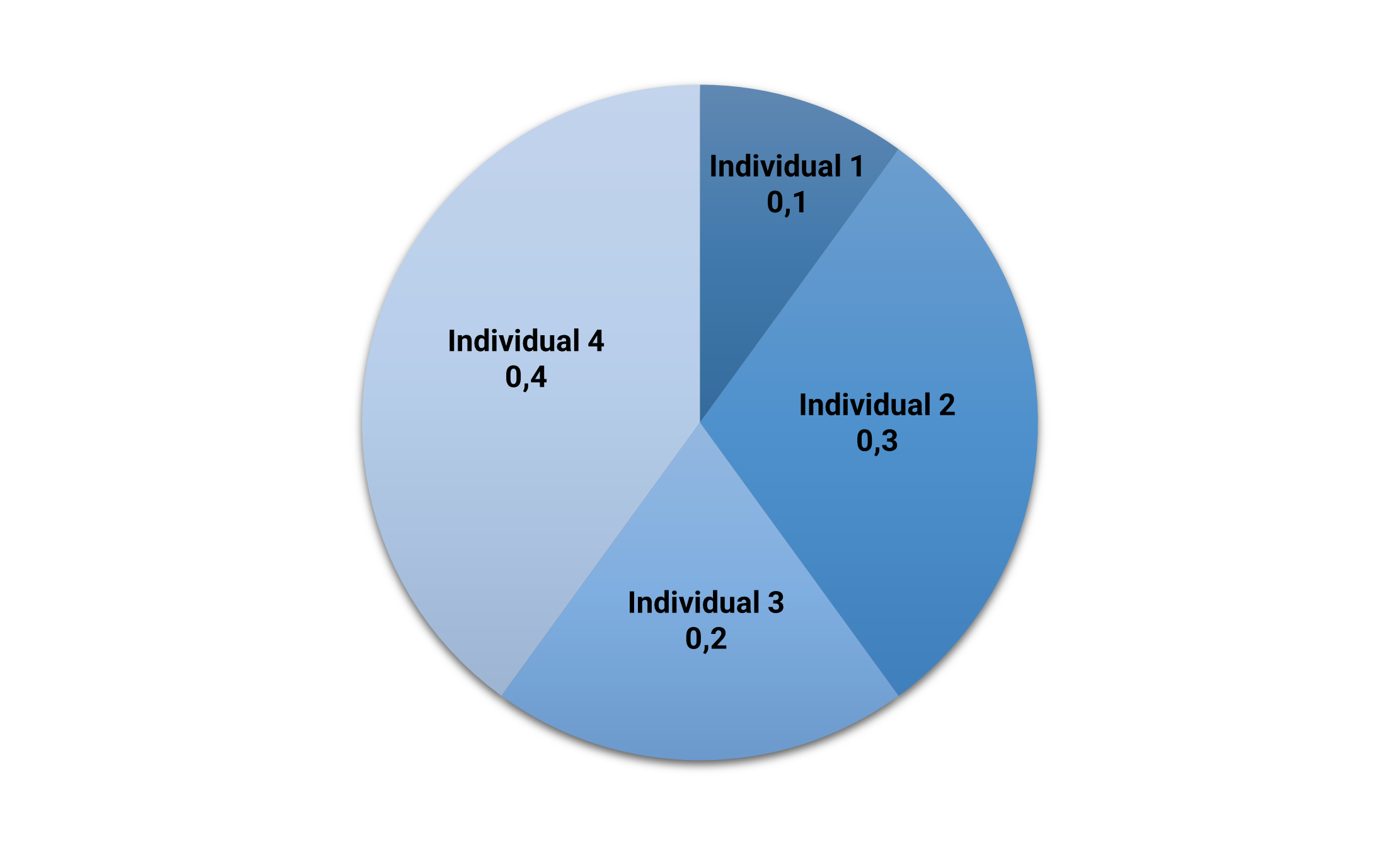
As we can see, the fittest individual (#4) is the one who has the most significant area (40%). Conversely, the least fitted individual (#1) has the smallest area (10%).
3. Selection operator
After a fitness assignment has been performed, the selection operator chooses the individuals that recombine for the next generation.
The individuals most likely to survive are those more fitted to the environment. Therefore, the selection operator selects the individuals according to their fitness level. The number of selected individuals is N/2, being N the population size.
Elitist selection makes the fittest individuals survive directly for the next generation. The elitism size controls the number of directly selected individuals, and it is usually set to a small value (1,2,…).
One of the most used selection methods is the roulette wheel. This method places all the individuals on a roulette, with areas proportional to their fitness, as we saw above. Then, it turns the roulette and selects the individuals at random. The corresponding individual is selected for recombination.
The following figure illustrates the selection process for our example.
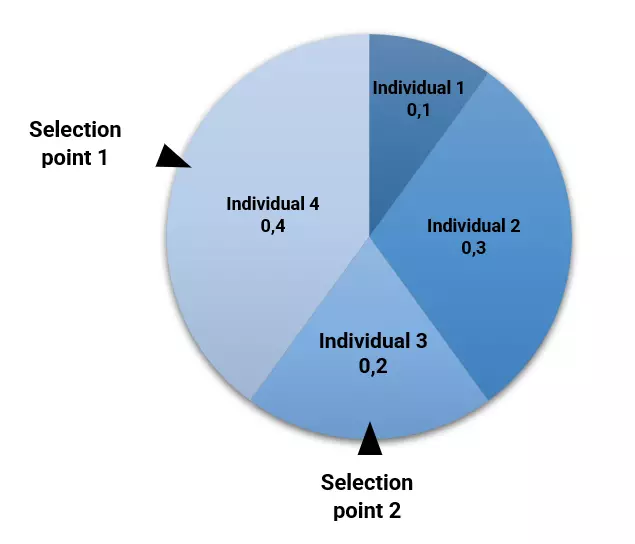
In this case, neural network #4 has been selected by elitism, and #3 has been selected by the roulette wheel. Note that, although individual #2 has more fitness than #3, it has not been selected due to the stochastic nature of the genetic algorithm.
Here, the number of selected individuals is half of the population size.
4. Crossover operator
Once the selection operator has chosen half of the population, the crossover operator recombines the selected individuals to generate a new population.
This operator picks two individuals randomly from the previously selected and combines their features to get four offspring for the new population until the new population is the same size as the old one.
The uniform crossover method decides whether each offspring’s features come from one parent or another.
The following figure illustrates the uniform crossover method for our example.
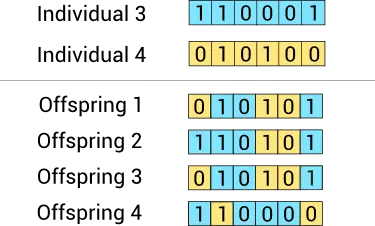
Here we have generated four offspring from two parents. Some features of each neural network correspond to one ancestor and others to the other.
In this case, the parents are directly replaced by the offspring. In this way, the population size remains constant.
5. Mutation operator
The crossover operator can generate offspring that are very similar to the parents. This might cause a new generation with low diversity.
The mutation operator solves this problem by randomly changing the value of some features in the offspring.
We generate a random number between 0 and 1 to decide if a feature is mutated. If the random number is lower than the mutation rate value, the operator flips that variable.
A standard value for the mutation rate is $dfrac{1}{m}$, where $m$ is the number of features. We mutate one feature of each individual (statistically) with that value.
The following image shows the mutation of one offspring of the new generation.

As we can see, the fourth input of the neural network has been mutated.
At this point, we have a new population.
Process and results
The whole fitness assignment, selection, recombination, and mutation process is repeated until a stopping criterion is satisfied.
Each generation will likely adapt more to the environment than the old one.
This chart shows the typical behavior of the mean selection error and the best selection error through generations. The example used is Breast Cancer Mortality example available in the blog.
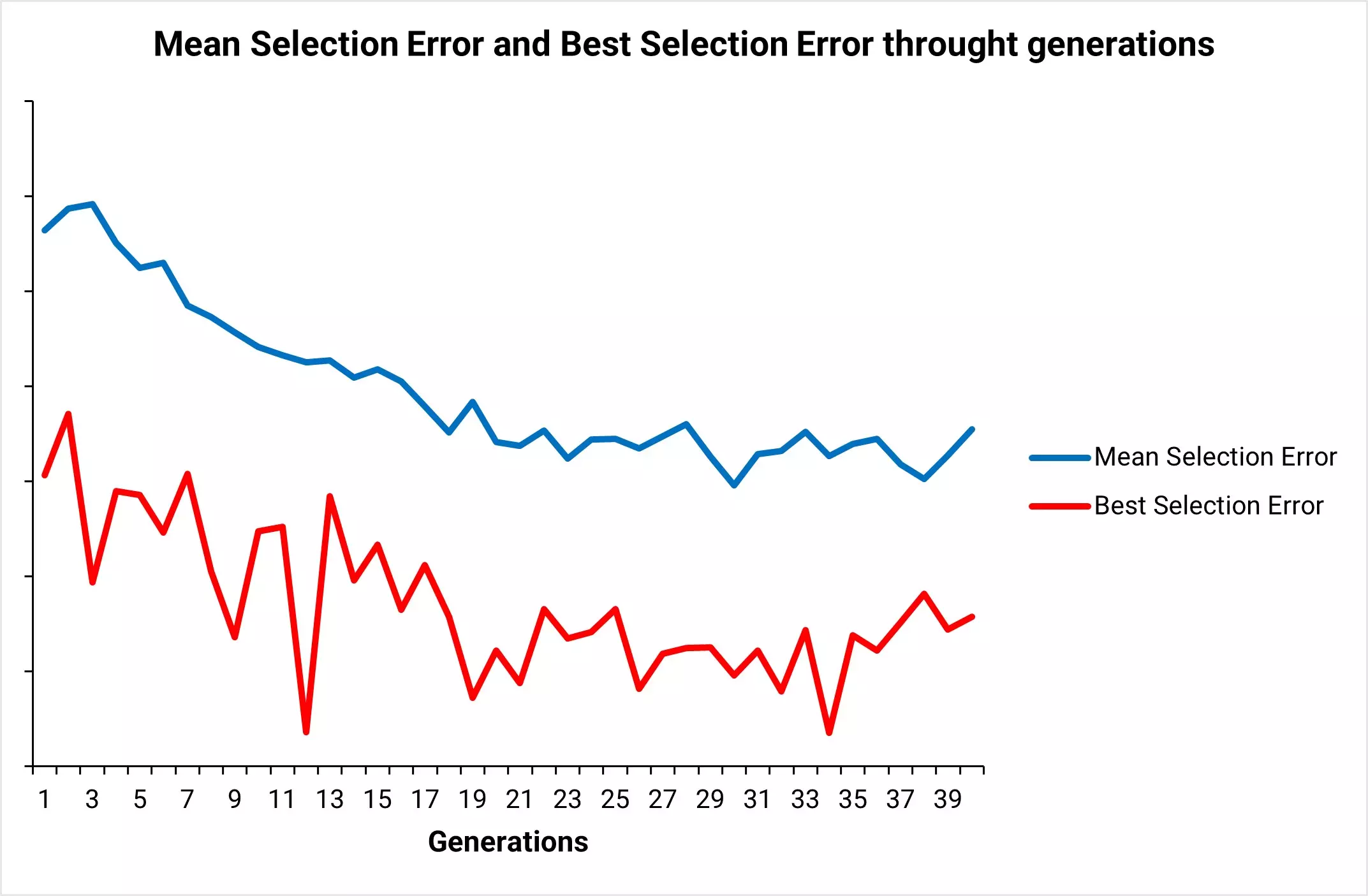
As we can see, the mean selection error at each generation converges to a minimum value.
The solution to this process is the best individual ever. This corresponds to the neural network with the smallest selection error among all those we have analyzed.
In our example, the best individual is the following:
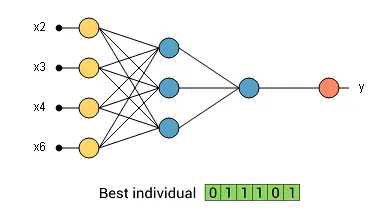
The above neural network is the selected one for our application.
Conclusions
Input selection is becoming a critical topic in machine learning. Many data sets contain many features, so we need to select the most useful ones to be included in the neural network.
One of the most advanced methods to do that is the genetic algorithm.
Some advantages of genetic algorithms are the following:
- They usually perform better than traditional feature selection techniques.
- Genetic algorithms can manage data sets with many features.
- They don’t need specific knowledge about the problem under study.
- These algorithms can be easily parallelized in computer clusters.
Some disadvantages are:
- Genetic Algorithms might be costly in computational terms.
Indeed, the evaluation of each individual requires training a model. - These algorithms can take a long time to converge since they are stochastic.
In conclusion, genetic algorithms can select the best subset of our model’s variables but usually require much computation.
Neural Designer implements a more advanced genetic algorithm than the one described in this post.
You can find it in the input selection section in the model selection panel.
Ready to apply feature selection with genetic algorithms to your own projects? Download Neural Designer and put these advanced concepts into practice without complex coding