Introduction
Breast cancer is one of the most common malignancies, and early detection is essential to improve outcomes.
Fine needle aspiration (FNA) biopsies are commonly used, but interpretation can be complex.
Neural networks analyze cellular features from digitized images to assist clinicians.
Using the University of Wisconsin dataset, our model reached 98.5% accuracy and 0.997 AUC, showing the potential of AI to complement expertise, reduce uncertainty, and improve diagnostic decisions.
Healthcare professionals can test this methodology with Neural Designer’s trial version.
Contents
The following index outlines the steps for performing the analysis.
1. Model type
The variable to be predicted can have two values (malignant or benign tumor). Therefore, this is a binary classification project.
The goal is to model the probability of a malignant tumor conditioned on the fine needle aspiration (FNA) test features using artificial intelligence and machine learning.
2. Dataset
Data source
The breast_cancer.csv dataset (683 instances, 10 variables) for a binary classification problem (target: 0 or 1).
Variables
Cell structure
clump_thickness (1–10) – Benign cells form monolayers; malignant cells form multilayers.
cell_size_uniformity (1–10) – Cancer cells vary in size and shape.
cell_shape_uniformity (1–10) – Cancer cells vary in shape and size.
single_epithelial_cell_size (1–10) – Enlarged epithelial cells may be malignant.
bare_nuclei (1–10) – Nuclei without cytoplasm, often in benign tumors.
bland_chromatin (1–10) – Uniform chromatin in benign cells; coarse in cancer cells.
normal_nucleoli (1–10) – Small in normal cells, enlarged in cancer cells.
Cell behaviour
marginal_adhesion (1–10) – Loss of adhesion is a sign of malignancy.
mitoses (1–10) – High values indicate uncontrolled cell division.
- diagnose (0 or 1) – Benign (0) or malignant (1) breast lump.
Instances
The dataset’s instances are split into training (60%), validation (20%), and testing (20%) subsets by default.
You can adjust them as needed.
Variables distributions
Also, we can calculate the distributions for all variables.
The following figure shows a pie chart with the numbers of malignant (1) and benign (0) tumors in the data set.
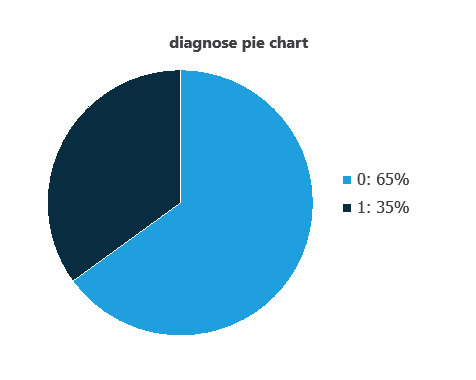
As depicted in the image, malignant tumors represent 35% of the samples, and benign tumors represent approximately 65%.
Inputs-targets correlations
The inputs-targets correlations indicate which factors most influence whether a tumor is malignant or benign and, therefore, are more relevant to our analysis.
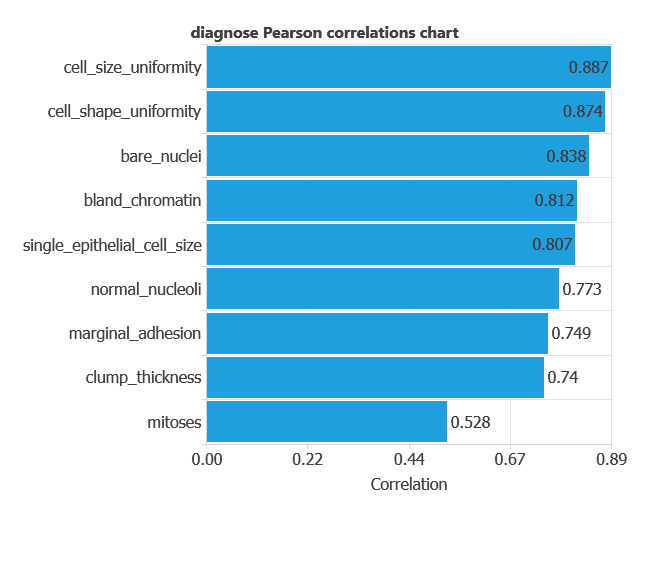
Here, the most correlated variables with malignant tumors are cell size uniformity, cell shape uniformity, and bare nuclei.
3. Neural network
A neural network is an artificial intelligence model inspired by how the human brain processes information.
It is organized in layers: the input layer receives the variables, and the output layer provides the probability of belonging to a given class.
The network uses historical data to learn patterns distinguishing benign from malignant tumors.
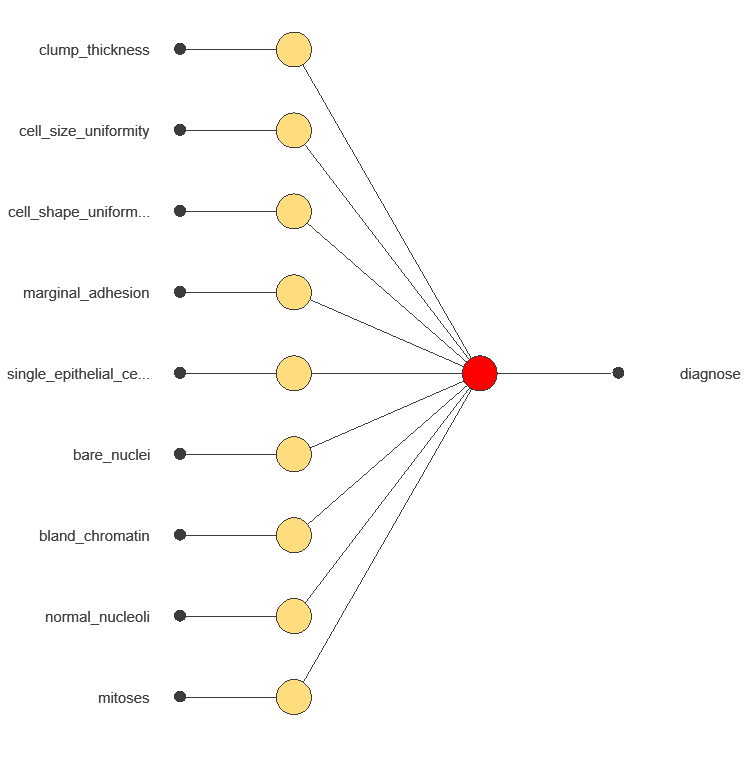
The network processes nine diagnostic variables and produces a single output: the probability that the tumor is malignant.
The connections illustrate how each variable contributes to the prediction.
4. Training strategy
Training a neural network involves defining a loss function to measure errors and an optimization algorithm to adjust the model.
The goal is to help the network learn from data while avoiding overfitting, so it can perform well on new cases.
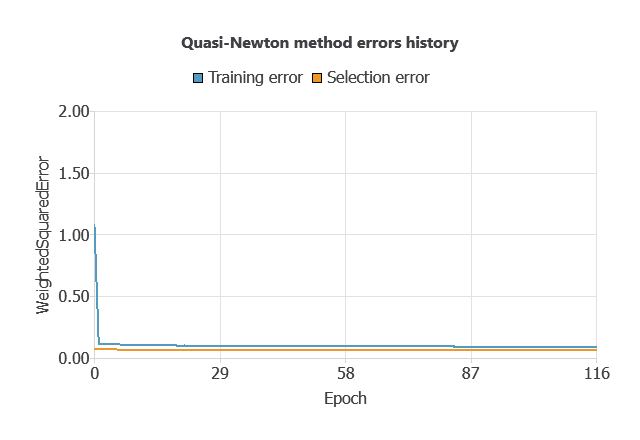
The network was trained to minimize errors while avoiding overfitting, achieving stable performance on new cases (training error 0.054, validation error 0.072).
5. Testing Analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network.
ROC curve
The ROC curve is a standard tool to evaluate a classification model, showing how well it distinguishes between two classes by comparing predicted results with actual outcomes.
A random classifier scores 0.5, while a perfect classifier scores 1.
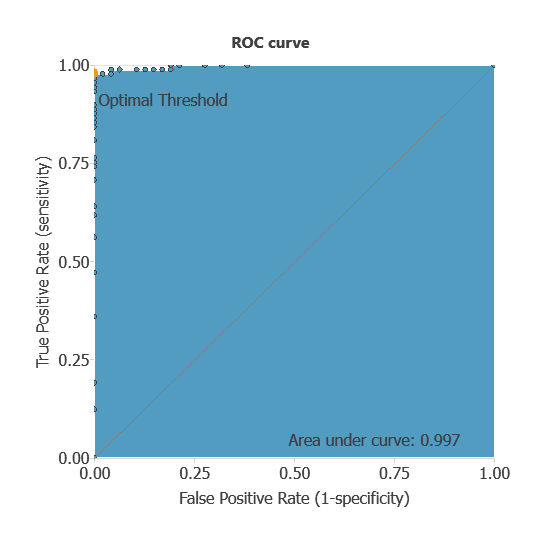
At a 0.5 threshold, the model achieved an AUC of 0.997, indicating excellent discrimination between benign and malignant tumors.
Confusion matrix
The confusion matrix shows the model’s performance by comparing predicted and actual diagnoses. It includes:
- true positives – tumors correctly identified as malignant
- false positives – benign tumors incorrectly identified as malignant
- false negatives – malignant tumors incorrectly identified as benign
- true negatives – tumors correctly identified as benign
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 47 | 0 |
| real negative | 2 | 87 |
Using a classification threshold of 0.5, 98.53% of cases were correctly classified and 1.47% were misclassified.
Binary classification
Using a classification threshold of 0.5, the performance of this binary classification model is summarized with standard measures:
Accuracy: 98.5% of tumors were correctly classified.
Error rate: 1.5% of cases were misclassified.
Sensitivity: 100% of malignant tumors were correctly identified.
Specificity: 98% of benign tumors were correctly identified.
The model correctly identifies nearly all malignant and benign tumors, confirming its high diagnostic performance.
6. Model deployment
Once validated, the model can be deployed to predict malignancy probabilities for new patients.
In deployment mode, healthcare professionals can use the model as a reliable diagnostic support tool for classifying new patients.
The Neural Designer software exports the trained model automatically, making it easy to integrate into clinical practice.
Conclusions
The breast cancer diagnostic model, developed with the University of Wisconsin dataset, showed excellent performance (AUC = 0.997, accuracy = 98.5%) in distinguishing benign from malignant tumors.
Key features—cell size and shape uniformity, and bare nuclei—align with pathological criteria, confirming clinical validity.
With strong generalization capacity, this neural network can serve as a valuable decision-support tool, enhancing early detection, complementing FNA biopsy interpretation, and improving diagnostic accuracy in clinical practice.
References
- We have obtained the data for this problem from the UCI Machine Learning Repository.
- Wolberg, W.H., & Mangasarian, O.L. (1990). Multisurface method of pattern separation for medical diagnosis applied to breast cytology. In Proceedings of the National Academy of Sciences, 87, 9193–9196.
- Zhang, J. (1992). Selecting typical instances in instance-based learning. In Proceedings of the Ninth International Machine Learning Conference (pp. 470–479). Aberdeen, Scotland: Morgan Kaufmann.
