There are numerous repositories with a large number of datasets for machine learning.
This post introduces a family of datasets known as the Rosenbrock Dataset Suite. The objective is to facilitate benchmarking of machine learning platforms.
Contents
Introduction
Data capacity tests
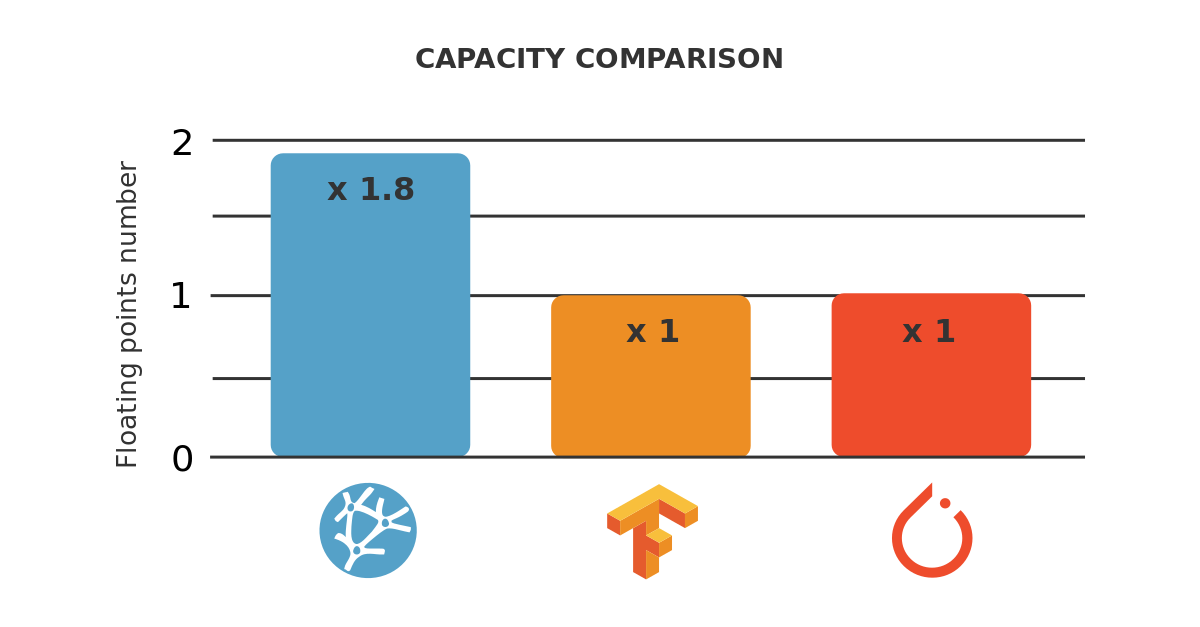
The data capacity of a machine learning platform can be defined as the largest dataset that it can process.
In this way, the tool should perform all the essential tasks with that dataset.
Data capacity can be measured as the number of samples that a machine learning platform can process for a given number of variables.
The most significant drawback is that they usually have a fixed number of variables and samples. This makes it difficult to test how a machine learning platform behaves with different dataset sizes.
Training speed tests
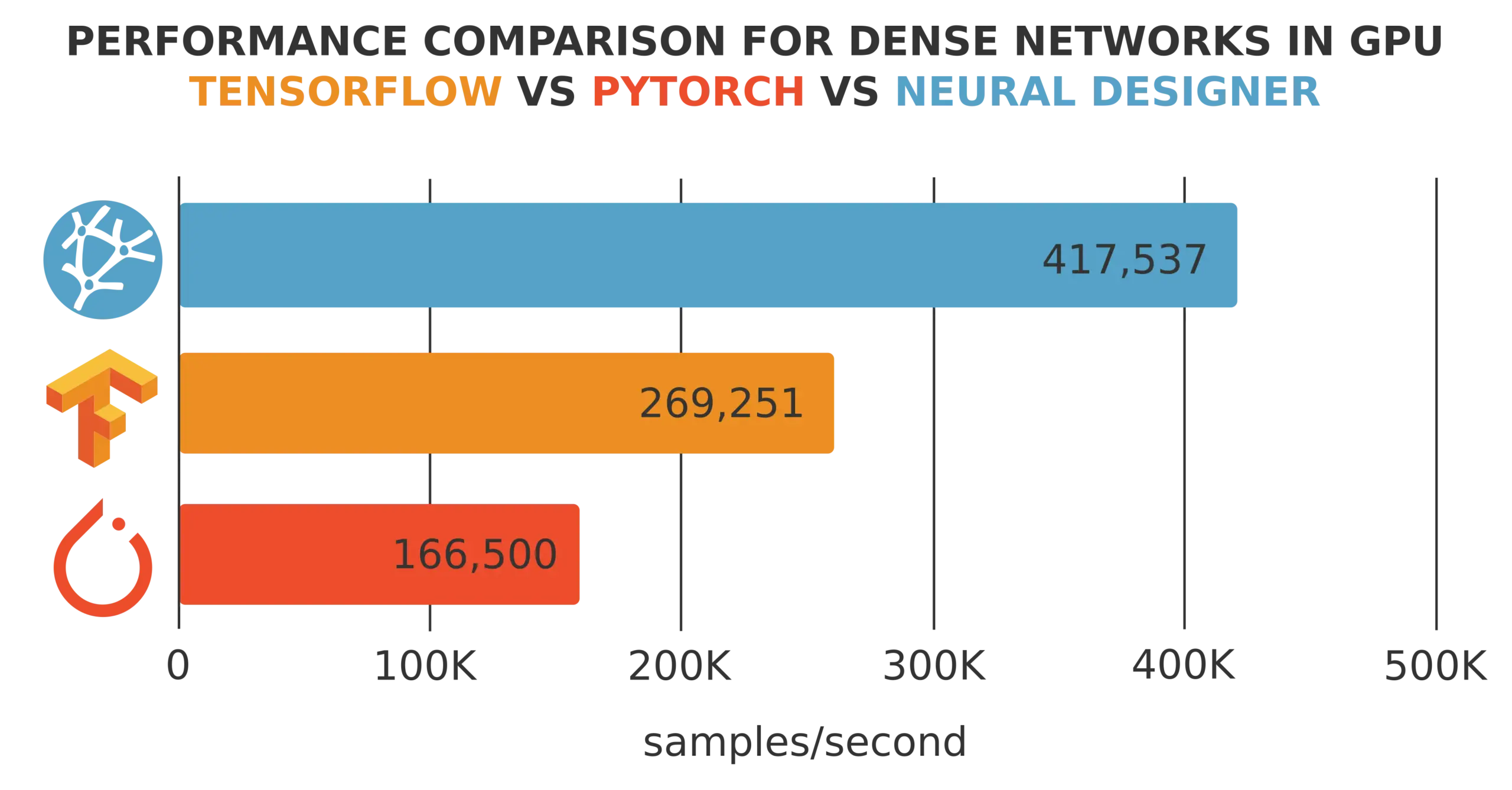
Training speed is defined as the number of samples per second that a machine learning platform processes during training.
The training speed depends very much on the dataset size. For instance, CPUs might provide faster training than GPUs for small datasets and slower training for big datasets.
Therefore, we need to generate datasets with arbitrary variables and samples to see how these sizes affect training performance.
Model precision tests
Precision can be defined as the mean error of a model against a testing data set.
Most real datasets are noisy. This means that the full fit of the model to the data cannot be verified.
Therefore, it is desirable to have datasets with which we can potentially build models with zero error.
Inference speed tests
The inference speed is the time to calculate the outputs as a function of the inputs. Inference speed is measured as the number of samples per second.
As before, we need to generate datasets with an arbitrary number of variables and samples to see how these sizes affect training performance.
Rosenbrock function
The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960. It is also known as Rosenbrock’s valley or Rosenbrock’s banana function.
It is used as a performance test problem for optimization algorithms.
In mathematical optimization, n is the number of samples, and m is the number of input variables.
$$x_{i,j} = rand(-1,+1)$$
$$y_{j} = sum_{i=1}^{n-1}left[ 100left(x_{i+1}-x_{i}^{2} right)^{2}+left(1-x_{i} right)^{2} right]$$
As the outputs from the Rosenbrock function are real values, this dataset suite is suitable for approximation problems.
Therefore, we cannot test the performance of classification or forecasting applications with that.
The Rosenbrock dataset suite allows the creation of datasets with any number of variables and samples. Thus, this suite is perfect for performing data capacity, training speed, and inference speed tests.
The Rosenbrock data is extracted from a deterministic function with a pretty complex shape. It should be possible to build a machine learning model of that function with any desired degree of accuracy. Therefore, Rosenbrock datasets are ideal for model precision tests.
C++ code
The following code shows how to generate a Rosenbrock dataset using C++.
// System includes
#include <iostream>
#include <fstream>
#include <string>
#include <random>
using namespace std;
int main(void)
{
cout << "Rosenbrock Dataset Generator." << endl;
const int inputs_number = 2;
const int samples_number = 10000;
const string filename = "G:/R__" + to_string(samples_number)+ "_samples_"+ to_string(inputs_number) + "_inputs.csv";
float inputs[inputs_number];
default_random_engine generator;
uniform_real_distribution<float> distribution(-1.0, 1.0);
ofstream file(filename);
for(int j=0; j < samples_number; j++)
{
float rosenbrock = 0.0;
for(int i=0; i < inputs_number; i++)
{
inputs[i] = distribution(generator);
file << inputs[i] << ",";
}
for(int i = 0; i< inputs_number - 1; i++)
{
rosenbrock +=
(1 - inputs[i])*(1 - inputs[i])
+ 100*(inputs[i+1]-inputs[i] * inputs[i])*
(inputs[i+1]-inputs[i]*inputs[i]);
}
file << rosenbrock << endl;
}
file.close();
return 0;
}
Python code
You can also generate a Rosenbrock dataset with the following Python code.
import numpy as np
import pandas as pd
import random
samples_number = 10000
inputs_number = 2
distribution = random.uniform(-1, 1)
inputs = np.random.uniform(-1.0, 1.0, size = (samples_number, inputs_number))
rosenbrock = []
for j in range (samples_number):
r = 0
for i in range(inputs_number-1):
r += (1.0 - inputs[j][i])*(1.0 - inputs[j][i])+100.0*((inputs[j][i+1]-inputs[j][i]*inputs[j][i])*(inputs[j][i+1]-inputs[j][i]*inputs[j][i]))
rosenbrock.append(r)
data = pd.concat([pd.DataFrame(inputs),pd.DataFrame(rosenbrock)], axis=1)
filename = "G:/R_" + str(samples_number)+ "_samples_"+ str(inputs_number) + "_variables_python.csv";
data.to_csv(filename,index = False,sep = ",")
Notice that the data is normalized between [-1,1].
Datasets download
We provide the following datasets:
| RowsColumns | 10 | 100 | 1000 |
|---|---|---|---|
| 1000 | rosenbrok_103_10.csv | rosenbrok_103_102.csv | rosenbrok_103_103.csv |
| 10000 | rosenbrok_104_10.csv | rosenbrok_104_102.csv | rosenbrok_104_103.csv |
| 100000 | rosenbrok_105_10.csv | rosenbrok_105_102.csv | rosenbrok_105_103.csv |
| 1000000 | rosenbrok_106_10.csv | rosenbrok_106_102.csv | rosenbrok_106_103.csv |
Conclusions
This blog introduces a function to measure machine learning platforms’ data capacity, training speed, model accuracy, and inference speed.
Rosenbrock datasets have a firm consistency and do not have noise. For this reason, it is a powerful alternative to datasets from popular repositories for benchmarking.
The data science and machine learning platform Neural Designer contains many utilities to perform descriptive, diagnostic, predictive, and prescriptive analytics easily.
You can download Neural Designer now and try it for free.