In machine learning, a variable refers to a feature or attribute used as input for training and making predictions. In this post, we describe the different types of variables (numerical, categorical, etc.) and their possible uses within a model (input, target, etc.).
Contents
1. Definition
A variable can be anything that can be measured or counted, such as a number, trait, or personality trait. It’s an element that defines something: a person, place, object, or idea. The value of the variable may vary from one sample to another. For example, variables can represent many different things: physical measurements (temperature, speed, etc.), personal characteristics (gender, age, etc.), marketing dimensions (periodicity, frequency, etc.), pixel values, etc.
In machine learning, the variables are the columns of the data matrix. A variable is a vector $v in {R}^{p}$, where $p$ is the number of samples in the data set. In this regard, the data matrix contains $q$ variables,
$\begin{eqnarray}
v_{i} := column_{i}(d), \quad i=1,\ldots,q.
\end{eqnarray}$
We can categorize variables according to the type of data or their use in the model.
2. Variable types
We can classify the different types of variables as numeric, ordinal, binary, categorical, date-time, or id.
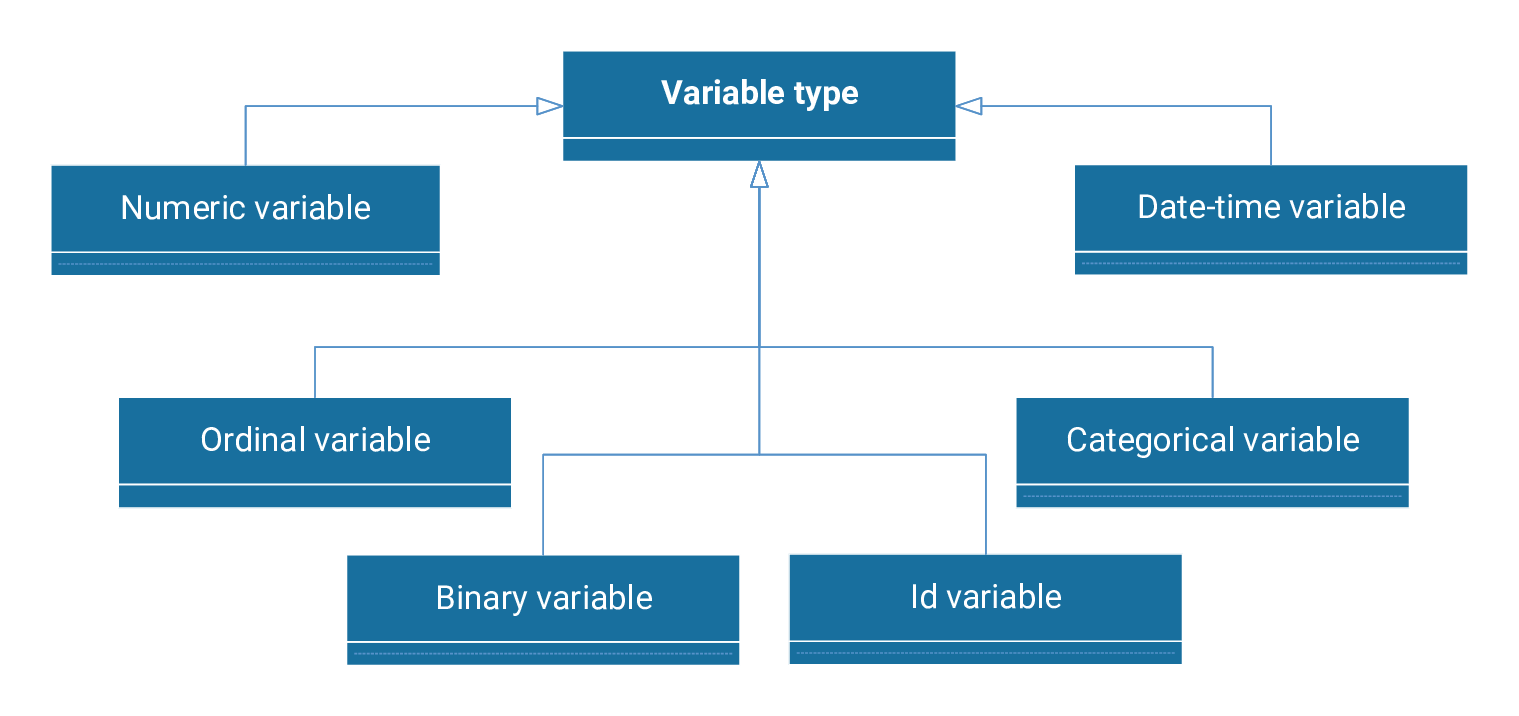
Below, we describe each of these six types of variables.
Numeric variables
Numeric variables have values that describe a measurable quantity as a number, like ‘how many’ or ‘how much.’ They are typically obtained by measuring (i.e., continuous) or counting (i.e., discrete). For that, we can describe numeric variables as either continuous or discrete.
We do not need to treat numeric variables before including them in the data matrix since they are already actual values.
Ordinal variables
Ordinal variables are those in which we can establish a precise order. For example, the education level (elementary school, high school, graduate degree) or the economic status (low, medium, high) are ordinal variables.
We can easily codify ordinal values as numeric values by sorting them according to their order. For example, we can assign the number $1$ to the first value, $2$ to the second one, $3$ to the third one, and so on.
Binary variables
Binary variables are those that have two classes.
They usually indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, a patient may be positive or negative for a given disease.
Another example is that a customer may or may not have purchased a product. In these cases, we label the positive value as $1$ and the negative value as $0$.
Categorical variables
Data consisting of a limited number of possible values can be considered categorical data. Categorical variables do not have an exact order. Categorical data can be viewed as aggregated information divided into groups. For example, marital status is a categorical variable whose values are single, married, and divorced.
Encoding categorical data is converting categorical data into integer format so that the data with converted categorical values can be provided to the models to give and improve the predictions.
For the case of categorical variables with two classes, $C_1$, and $C_2$, we can codify one class as $0$ and the other as $1$.
Therefore, the number of resulting variables is just one. In this way, the value for a sample $j$ is
$\begin{eqnarray}
\boxed{v_{j} = \left\{ \begin{array}{ll}
0 & \textrm{$x_{i,j} \in C_{1}$,}\\
1 & \textrm{$x_{i,j} \in C_{2}$,}
\end{array} \quad i=1, \ldots,q. \right.}
\end{eqnarray}$
We must code the data with the one-hot encoding scheme if the categorical variable has more than two classes, $C_{1}, ldots, and C_{m}$.
In this encoding, each category of any categorical variable receives a new variable. It assigns each category with binary numbers (0 or 1).
The following table illustrates the one-hot encoding.
| $C_1$ | $C_2$ | $C_3$ | … | $C_q$ |
|---|---|---|---|---|
| 1 | 0 | 0 | … | 0 |
| 0 | 1 | 0 | … | 0 |
| 0 | 0 | 1 | … | 0 |
| … | … | … | … | … |
| 0 | 0 | 0 | … | 1 |
After one-hot encoding, the number of resulting variables is the number of categories.
In this way, the variables of a sample $i$ are
$\begin{eqnarray}
\boxed{v_{j} = \left\{ \begin{array}{ll}
0 & \textrm{$x_{j,i} \notin C_{k}$,}\\
1 & \textrm{$x_{j,i} \in C_{k}$,}
\end{array} \quad i=1, \ldots,q. \right.}
\end{eqnarray}$
Date-time variables
A date-time variable encodes a calendar date and a clock time. It includes in single string information about the year, month, day, and second.
Human-readable date/time variables are converted to Unix timestamp variables. Unix timestamps are a way to track time as the total number of seconds running.
These variables are not included in the model.
Constant variables
Constant variables are those columns in the data matrix that always have the same value. They should be set as unused since they do not provide any information to the model but increase its complexity.
Id variables
The id variables identify the samples. These variables are not part of the model.
Example: Bank marketing variable types
A banking institution conducts a customer segmentation study to identify the people most likely to be interested in a specific product or service. In this way, the bank creates a model to predict which customers will subscribe to a long-term deposit and which will not.
The variables included in the dataset are the following.
- The variable $age$ is numeric. It takes values such as 18, 45, 72, etc.
- The variable $marital status$ is categorical. It takes values divorced, married, and single.
- The variable $default$ is binary.
- The variable $balance$ is numeric. It takes values between -3313 and 71188.
- The variable $housing$ is binary.
- The variable $loan$ is binary.
- The variable $contact$ is binary.
- The variable $day$ is numeric. It takes the different values of the days of the month, from 1 to 31.
- The variable $month$ is numeric. It takes the different values of the month of the year, from 1 to 12.
- The variable $campaign$ is numeric. It takes values between 1 and 50.
- The variable $last contact$ is numeric. It takes values between 1 and 871.
- The variable $previous contacts$ is numeric. It takes values between 0 and 25.
- The variable $past outcome$ is binary.
- The variable $conversion$ is binary.
3. Variable uses
We can discuss input, target, or unused variables regarding their use.
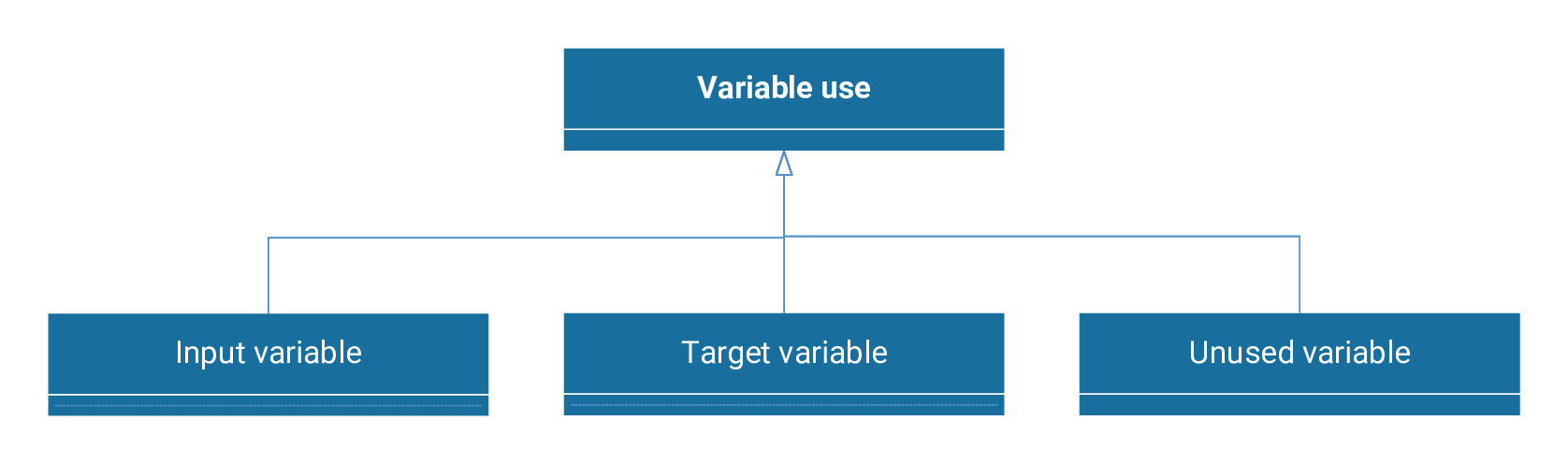
Each of these three uses of variables is described below.
Input variables
Input variables are the independent variables in the model. They are also called features or attributes.
Input variables are denoted $x$. The number of input variables in a data matrix is denoted $n$.
Target variables
Target variables are the dependent variables in the model.
Target variables are denoted $t$. The number of target variables in a data matrix is denoted $m$.
In approximation problems, targets are continuous variables (power consumption, product quality, etc.).
In classification problems, targets are categorical variables (fault, churn, etc.). In this type of application, targets are also called categories or labels.
Unused variables
Unused variables are neither inputs nor targets. We can set a variable to Unused when it does not provide any information to the model (id number, address, etc.).
In this regard, we can define a variable using a vector as follows,
$\begin{eqnarray}
variables\_use = \{ input \lor target \lor unused \}^{q}.
\end{eqnarray}$
The size of this vector is $q$, the number of variables in the data set.
Note that a variable cannot have two uses at the same time. For example, we cannot use a variable as input and as output at the same time.
Conclusions
Variables are the columns of the data matrix. We have different variables depending on whether we classify them by type or use. It is advisable to carry out a study of these variables before the model.
Tutorial video
You can watch the video tutorial to help you complete this article.