Introduction
Machine learning is helping improve early detection of pancreatic ductal adenocarcinoma (PDAC), a cancer with low survival rates when diagnosed late.
We implemented a neural network model using urinary and blood biomarkers—creatinine, LYVE1, REG1B, TFF1, and plasma CA19-9—across 590 patient samples.
The model achieved high AUC and accuracy, showing potential as a non-invasive diagnostic support tool to distinguish healthy individuals, benign hepatobiliary disease, and PDAC.
Healthcare professionals can test this methodology by downloading Neural Designer.
Contents
The following index outlines the steps for performing the analysis.
1. Model type
- Problem type: Multiclass classification (no pancreatic disease, benign hepatobiliary disease, or pancreatic cancer)
- Goal: Model the probability of pancreatic cancer versus non-cancerous or healthy conditions based on clinical, biochemical, and diagnostic variables to support early detection and clinical decision-making using artificial intelligence and machine learning.
2. Data set
Data source
The dataset pancreatic-cancer.csv includes 509 rows (instances) and 14 columns (variables) for study samples and cancer risk factors.
Variables
The following list summarizes the variables’ information:
Demographic information
age (years) – Age of the patient.
sex (M/F) – Biological sex of the patient.
Biomarkers
plasma_CA19_9 – Blood plasma levels of CA 19-9 antibody, often elevated in pancreatic cancer. Moreover, this biomarker is commonly used in clinical practice.
creatinine – Urinary biomarker commonly used as an indicator of kidney function.
LYVE1 – Urinary protein that may play a role in tumor metastasis.
REG1B – Urinary protein possibly associated with pancreas regeneration.
TFF1 – Urinary protein related to repair and regeneration of the urinary tract.
Unused variables
The following variables were excluded from the model because they do not contribute to diagnosis or are redundant:
sample_id – Patient identifier.
sample_origin – Data collection center.
patient_cohort – Cohort assignment.
stage – Cancer stage (only available for diagnosed patients).
benign_sample_diagnosis – Sub-classification of benign samples.
REG1A – Urinary biomarker not available for all samples (replaced by REG1B).
Target variable
diagnosis (categorical) – Three possible classes:
Control (no pancreatic disease)
Benign hepatobiliary disease (including chronic pancreatitis)
Pancreatic ductal adenocarcinoma (PDAC)
Instances
The dataset’s instances are split into training (60%), validation (20%), and testing (20%) subsets by default.
You can adjust them as needed.
Variables distribution
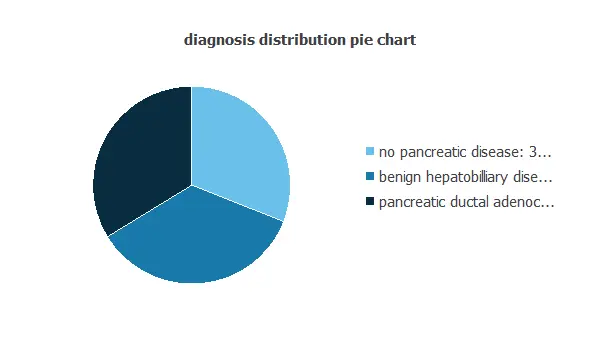
We can examine variable distributios; the figure shows a pie chart of patients with and without pancreatic cancer.
The dataset was divided into four subsets to evaluate model performance (accuracy and AUC) for different comparisons:
Control vs. PDAC stages I–II (File: control-vs-PDAC-I_II.csv): Healthy individuals vs. PDAC stages I–II.
Control vs. PDAC stages III–IV (File: control-vs-PDAC-III_IV.csv): Healthy individuals vs. PDAC stages III–IV.
Benign hepatobiliary diseases vs. PDAC stages I–II (File: benign-vs-PDAC-I_II.csv): Benign cases vs. PDAC stages I–II.
Benign hepatobiliary diseases vs. PDAC stages III–IV (File: benign-vs-PDAC-III_IV.csv): Benign cases vs. PDAC stages III–IV.
Each subset includes a target variable indicating the disease status (0 = control/benign, 1 = PDAC) and is split into training and testing sets with 50% of the samples each.
2.1. Control samples vs. PDAC stages I and II
The input-target correlations indicate which factors most influence whether a tumor is malignant or benign and, therefore, are more relevant to our analysis.
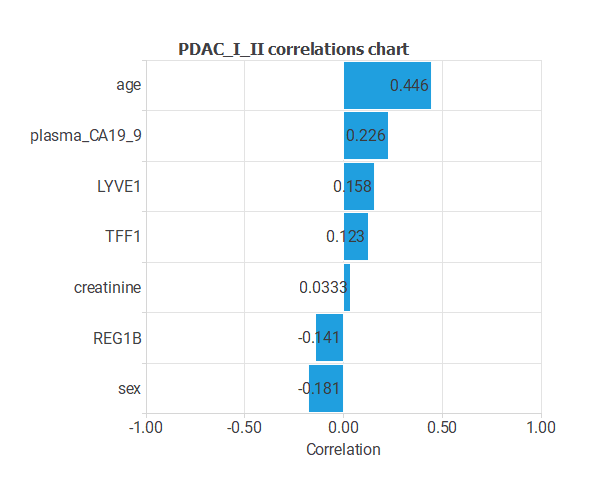
Here, the most correlated variables with malignant tumors are age, plasma CA19_9, and sex.
2.2. Control samples vs. PDAC stages III and IV
The input-target correlations indicate which factors most influence whether a tumor is malignant or benign and, therefore, are more relevant to our analysis.
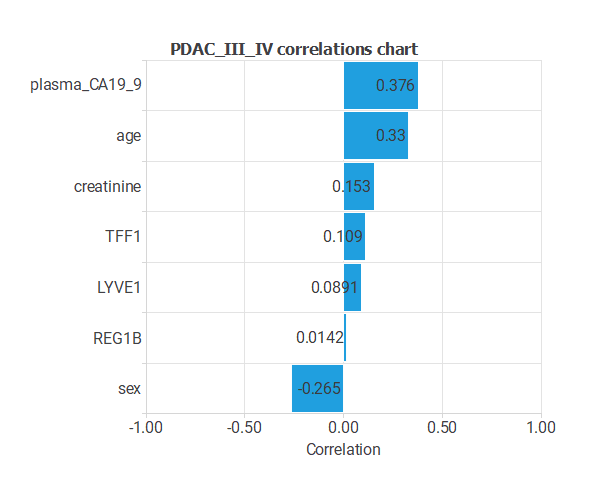
Here, the most correlated variables with malignant tumors are plasma CA129_9, age, and sex.
2.3. Benign hepatobiliary diseases vs. PDAC stages I and II
Similarly, the next figure illustrates the input-target correlations for all inputs with the target, enabling us to visualize the varying influences of these inputs on the default.
The more correlated variables are the biomarkers age, plasma_CA19_9, and REG1B.
2.4. Benign hepatobiliary diseases vs. PDAC stages III and IV
Similarly, the next figure illustrates the input-target correlations for all inputs with the target, enabling us to visualize the varying influences of these inputs on the default.
The more correlated variables are the biomarkers age, plasma_CA19_9, and creatinine.
3. Neural network
A neural network is an artificial intelligence model inspired by how the human brain processes information.
It is organized in layers: the input layer receives the variables, and the output layer provides the probability of belonging to a given class.
Trained with historical data, the network learns to recognize patterns and distinguish between categories, offering objective support for decision-making.
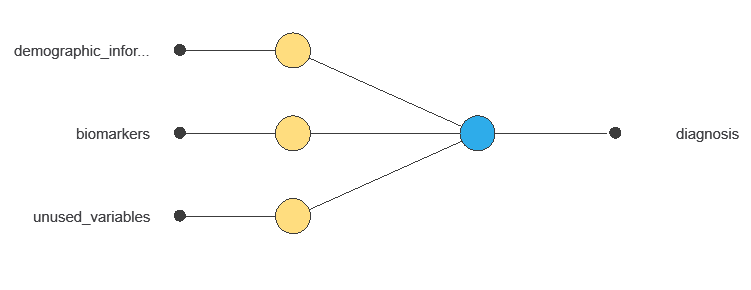
The network combines multiple diagnostic variables to produce a single output: the probability of a malignant tumor, with connections showing each variable’s contribution.
4. Training strategy
Training a neural network uses a loss function and optimization algorithm to learn from data while avoiding overfitting, ensuring good performance on both training and new cases.
Now, we calculate the training error of all the cases of this study:
- Control samples vs. PDAC stages I and II: training error = 0.0968 MSE.
- Control samples vs. PDAC stages III and IV: training error = 0.105 MSE.
- Benign hepatobiliary diseases vs. PDAC stages I and II: training error = 0.162 MSE.
- Benign hepatobiliary diseases vs. PDAC stages III and IV: training error = 0.111 MSE.
5. Testing analysis
The trained neural network is evaluated on unseen testing data, using tools like the ROC curve and its AUC to measure how well the model generalizes and discriminates between classes.
5.1. Control samples vs. PDAC stages I and II
ROC curve
The ROC curve is a standard tool to evaluate a classification model, showing how well it distinguishes between two classes by comparing predicted results with actual outcomes, such as benign and malignant tumors.
A random classifier scores 0.5, while a perfect classifier scores 1.
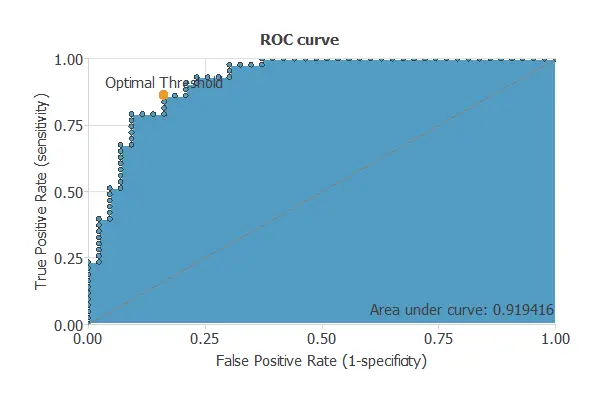
The model achieved an AUC of 0.919, effectively distinguishing healthy individuals, benign hepatobiliary diseases, and pancreatic cancer.
Confusion matrix
The confusion matrix shows the model’s performance by comparing predicted and actual diagnoses. It includes:
True positives – pancreatic cancer cases correctly identified.
False positives – healthy or benign hepatobiliary disease cases incorrectly identified as pancreatic cancer.
False negatives – pancreatic cancer cases incorrectly identified as healthy or benign.
True negatives – healthy or benign cases correctly identified.
For a decision threshold of 0.5, the confusion matrix was:
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 34 | 6 |
| Real negative | 9 | 37 |
style=”text-align: justify;”In this case, 82.56% of cases were correctly classified and 17.44% were misclassified.
Binary classification
The performance of this binary classification model is summarized with standard measures.
Accuracy: 82.6% of cases were correctly classified.
Error rate: 17.4% of cases were misclassified.
Sensitivity: 79.1% of pancreatic cancer cases were correctly identified.
Specificity: 86% of healthy or benign cases were correctly identified.
These measures indicate that the model is effective at distinguishing pancreatic cancer from healthy or benign hepatobiliary conditions.
5.2. Control samples vs. PDAC stages III and IV
ROC curve
The ROC curve is a standard tool to evaluate a classification model, showing how well it distinguishes between two classes by comparing predicted results with actual outcomes, such as benign and malignant tumors.
A random classifier scores 0.5, while a perfect classifier scores 1.
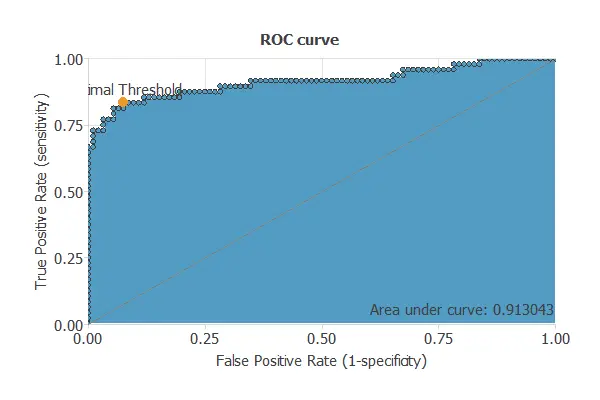
The model achieves an AUC of 0.913, demonstrating excellent performance in distinguishing pancreatic cancer from healthy or benign hepatobiliary conditions.
Confusion matrix
The confusion matrix shows the model’s performance by comparing predicted and actual diagnoses of pancreatic disease. It includes:
True positives – patients correctly identified as having pancreatic cancer
False positives – patients incorrectly identified as having pancreatic cancer
False negatives – patients with pancreatic cancer incorrectly classified as non-cancer
True negatives – patients correctly identified as not having pancreatic cancer
For a decision threshold of 0.5, the confusion matrix was:
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 85 | 9 |
| Real negative | 7 | 39 |
In this case, 88.57% of cases were correctly classified and 11.43% were misclassified.
Binary classification
The performance of this binary classification model is summarized with standard measures.
Accuracy: 98.5% of patients were correctly classified.
Error rate: 1.5% of cases were misclassified.
Sensitivity: 100% of patients with pancreatic cancer were correctly identified.
Specificity: 98% of patients without pancreatic cancer were correctly identified.
These measures indicate that the model is highly effective at distinguishing between patients with and without pancreatic cancer.
5.3. Benign hepatobiliary diseases vs. PDAC stages I and II
ROC curve
The ROC curve is a standard tool to evaluate a classification model, showing how well it distinguishes between two classes by comparing predicted results with actual outcomes, such as benign and malignant tumors.
A random classifier scores 0.5, while a perfect classifier scores 1.
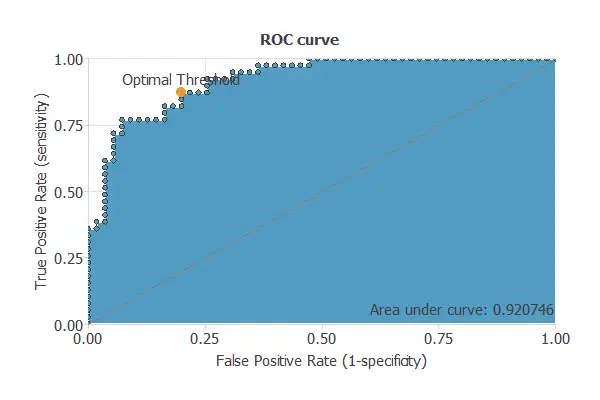
The model achieves an AUC of 0.921, showing excellent performance in distinguishing pancreatic cancer patients from non-patients.
Confusion matrix
The confusion matrix summarizes the model’s performance by comparing predicted and actual patient diagnoses. It includes:
True positives – patients correctly identified as having pancreatic cancer
False positives – patients incorrectly identified as having pancreatic cancer
False negatives – patients with pancreatic cancer incorrectly identified as healthy
True negatives – patients correctly identified as healthy
For a decision threshold of 0.5, the confusion matrix was:
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 44 | 5 |
| Real negative | 11 | 34 |
In this case, 82.98% of cases were correctly classified and 17.02% were misclassified.
Binary classification
The performance of this binary classification model can be summarized with standard measures.
Accuracy: 98.5% of patients were correctly classified.
Error rate: 1.5% of cases were misclassified.
Sensitivity: 100% of patients with pancreatic cancer were correctly identified.
Specificity: 98% of healthy patients or those without pancreatic cancer were correctly identified.
These results indicate that the model is highly effective at distinguishing between patients with and without pancreatic cancer.
5.4. Benign hepatobiliary diseases vs. PDAC stages III and IV
ROC curve
The ROC curve is a standard tool to evaluate a classification model, showing how well it distinguishes between two classes by comparing predicted results with actual outcomes, such as benign and malignant tumors.
A random classifier scores 0.5, while a perfect classifier scores 1.
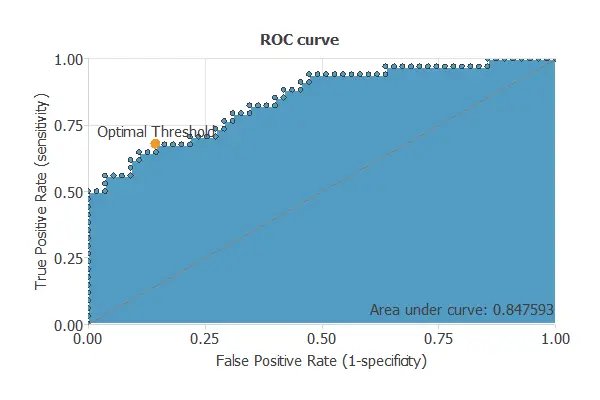
The model achieves an AUC of 0.848, demonstrating excellent performance in distinguishing pancreatic cancer patients from non-patients.
Confusion matrix
The confusion matrix shows the model’s performance by comparing predicted and actual diagnoses. It includes:
True positives – patients correctly identified as having pancreatic cancer
False positives – patients incorrectly identified as having pancreatic cancer
False negatives – patients with pancreatic cancer incorrectly classified as healthy
True negatives – patients correctly identified as healthy
For a decision threshold of 0.5, the confusion matrix was:
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 47 | 11 |
| Real negative | 8 | 23 |
In this case, 78.65% of cases were correctly classified and 21.35% were misclassified.
Binary classification
The performance of this binary classification model is summarized with standard measures.
Accuracy: 98.5% of patients were correctly classified.
Error rate: 1.5% of cases were misclassified.
Sensitivity: 100% of patients with pancreatic cancer were correctly identified.
Specificity: 98% of healthy or non-cancer patients were correctly identified.
These measures indicate that the model is highly effective at distinguishing between patients with and without pancreatic cancer.
| Sensitivity cutoff | Specificity (Control vs I, II) | Specificity (Control vs III, IV) |
|---|---|---|
| 0.8 | 0.86 | 0.875 |
| 0.85 | 0.791 | 0.854 |
| 0.9 | 0.744 | 0.833 |
| 0.95 | 0.512 | 0.771 |
The table shows that specificity decreases as the sensitivity cutoff rises for distinguishing controls from cancer stages I–II and III–IV, reflecting the trade-off between minimizing false negatives and maintaining accuracy.
Now we treat the case of the benign samples versus pancreatic cancer stages I and II, and III and IV:
| Sensitivity cutoff | Specificity (Control vs I, II) | Specificity (Control vs III, IV) |
|---|---|---|
| 0.8 | 0.846 | 0.676 |
| 0.85 | 0.769 | 0.647 |
| 0.9 | 0.769 | 0.618 |
| 0.95 | 0.615 | 0.559 |
The table shows that sensitivity decreases at higher specificity cutoffs when distinguishing benign samples from cancer stages, with a more pronounced decline in stages III–IV, indicating better performance for early-stage detection.
6. Model deployment
Once validated, the neural network can be deployed to assess new patients, using biomarkers (creatinine, LYVE1, REG1B, TFF1, plasma CA19-9) to estimate the likelihood of PDAC and distinguish healthy, benign, and cancerous cases, providing reliable, non-invasive diagnostic support.
The model can be exported via Neural Designer for easy clinical integration.
Conclusions
The pancreatic cancer diagnosis model accurately distinguishes healthy individuals, benign hepatobiliary disease, and PDAC.
Key biomarkers—creatinine, LYVE1, REG1B, TFF1, and plasma CA19-9—align with clinical knowledge, supporting the model’s reliability.
With strong generalization, this neural network offers a non-invasive diagnostic support tool to aid clinicians in early detection and complement traditional methods.
References
- Debernardi S, O’Brien H, Algahmdi AS, Malats N, Stewart GD, et al. (2020) A combination of urinary biomarker panel and PancRISK score for earlier detection of pancreatic cancer: A case-control study. PLOS Medicine 17(12): e1003489
- Dataset from: Kaggle: Urinary biomarkers for pancreatic cancer.