• 1.1. Approximation.
• 1.2. Classification.
• 1.3. Forecasting.
• 1.4. Auto association.
• 1.5. Text classification.

1.1. Approximation (or function regression)

An approximation can be regarded as the problem of fitting a function from data.

Here, the neural network learns from knowledge represented by a data set consisting of instances with input and target variables. The targets are a specification of the response to the inputs.

In this regard, the primary goal of an approximation problem is to model one or several target variables conditioned on the input variables.

The objective here is to estimate the value of y, knowing the value of x. The following figure illustrates an approximation problem.

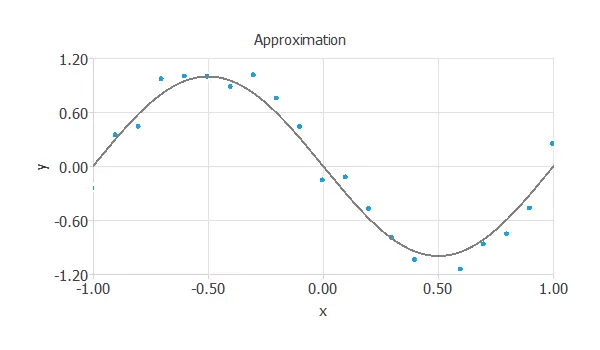
In approximation applications, the targets are usually continuous variables.
Some examples are the following:

• Model the strength of high-performance concretes.
• Predict the noise generated by airfoil blades.
• Predict the residuary resistance of sailing yachts.
• Predict the vascular adhesion of nanoparticles.
• Predict the electricity generated by combined cycle power plants.
• Forecast the power generated by a solar plant.
• Model wine preferences from physicochemical properties.

A common feature of most data sets is that the data exhibits an underlying systematic aspect, represented by some function, but is corrupted with random noise.

The objective is to produce a neural network that exhibits good generalization, or in other words, one that makes good predictions for new data.

The best generalization is obtained when the mapping represents the underlying systematic aspects of the data rather than capturing the specific details (i.e., the noise contribution).

1.2. Classification (or pattern recognition)

Classification can be stated as the process whereby a received pattern, characterized by a distinct set of features, is assigned to one of a prescribed number of classes.

The inputs here include features that characterize a pattern; the targets specify each pattern’s class.

The primary goal in a classification problem is to model the posterior probabilities of class membership, conditioned on the input variables.

The following figure illustrates a classification task. Here, we want to discriminate the class (circles or green squares) based on the x₁ and x₂ values of the object.

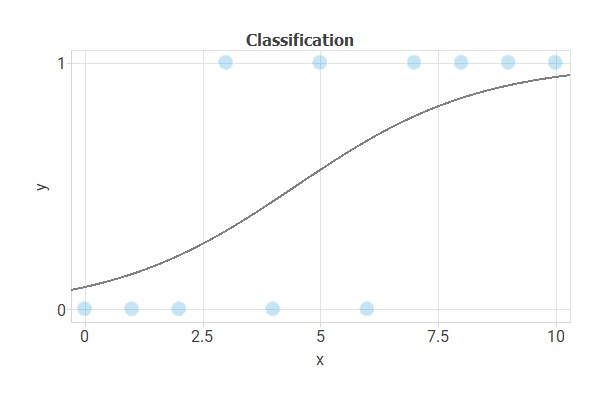
As before, the central goal is to design a neural network with good generalization capabilities. That is a model that can classify new data correctly.

We can distinguish between two types of classification models:

• Binary classification
• Multiple classification

Binary classification

In binary classification, the target variable is usually binary (true or false).

Some examples are to:

• Diagnose breast cancer from fine-needle aspirate images.
• Detect malfunctions liquid ultrasonic flowmeters.
• Detect forged banknotes.
• Reduce employee attrition.
• Increase the conversion rate of telemarketing campaigns in banks.
• Predict the probability of default of credit card clients.
• Detect diseased trees from remote sensing data.
• Target donors in blood donation campaigns.
• Diagnose acute inflammations of the urinary bladder.
• Predict the churn of customers in telecommunications companies.

Multiple classification

In multiple classifications, the target variable is usually nominal (class_1, class_2, or class_3).

Some examples are the following:

• Classify iris flowers from sepal and petal dimensions (setosa, versicolor or virginica).
• Recognize human activity on smartphones (walking, sitting, standing…).

1.3. Forecasting (or time series prediction)

Forecasting can be regarded as the problem of predicting the future state of a system from a set of past observations to that system.

A forecasting application can also be solved by approximating a function from a data set. In this type of problem, the data is arranged in a time series fashion. The inputs include data from past observations (predictors), and the targets include corresponding future observations (predictands).

The basic goal here is to model future observations conditioned on past observations.

The following figure illustrates a forecast application. The objective is to predict a step ahead y_t+1, based on the lags y_t, y_t-1,…

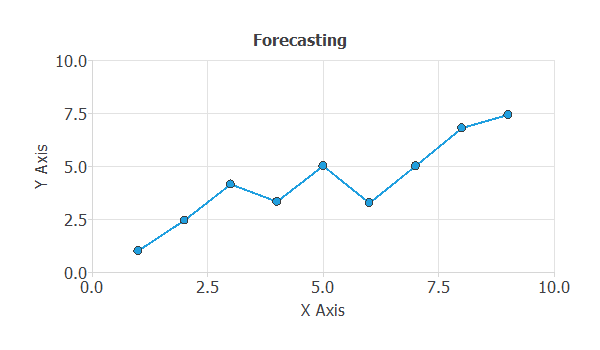
An example is to forecast the future sales of a car model as a function of past sales, marketing actions, and macroeconomic variables.

As always, good generalization is the central goal in forecasting applications.

1.4. Auto association

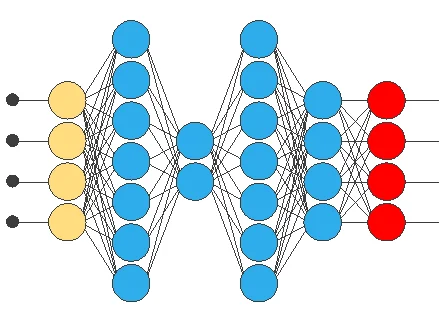
Auto-association models are those in which we use auto-associative neural networks to learn a compressed or reduced representation of the input data.

The following figure illustrates an auto-associative neural network:

Auto-association models are beneficial for unsupervised learning tasks, where the goal is to learn underlying patterns in the data without needing labeled examples. They can also be used for semi-supervised or supervised tasks where the model learns a representation of the normal data and then uses it to detect anomalies. Some examples of these uses are:

• Signal or failure detection: Detecting anomalies in sensor data, financial transactions, manufacturing processes, or medical vital signs by learning a representation of the normal data and using it to detect deviations.
• Recommender systems: Modeling user preferences and making recommendations.
• Denoising: Removing noise from images or other data by learning to reconstruct the original data from a noisy version.

In general, auto-association models are a powerful tool for various applications and have the potential to improve efficiency, reduce the complexity of the data, and provide a deeper understanding of the underlying patterns in the data.

1.5. Text classification

Text classification is a natural language processing task in which text data is classified into predefined categories or labels. The basic goal of a text classification problem is to model one or several target variables conditioned on the input text data.

The following figure illustrates a text classification problem. The objective here is to predict the category or label of a given text based on its content.

In text classification applications, the targets are usually discrete variables such as categories, labels, or sentiments.
Some examples are the following:

• Spam detection: Classifying emails as spam or not based on their content.
• Sentiment analysis: Classifying text data as positive, negative, or neutral based on the sentiment expressed.
• Topic classification: Classifying news articles into predefined topics such as politics, sports, technology, etc.
• Named entity recognition: Identifying and classifying named entities such as people, organizations, locations, etc.

A common feature of most text classification data sets is that text data exhibits an underlying systematic aspect, represented by certain patterns or features, but is also corrupted with random noise such as typos, grammar errors, or irrelevant information.

The objective is to produce a text classification model that exhibits good generalization, or in other words, one that makes good predictions for new text data.