This example uses machine learning to develop a classification method to detect tree wilt (Japanese oak wilt and Japanese pine wilt).
For that, we use satellite imagery. The accuracy obtained by the classification model is 89.2%.
Contents:
1. Application type
The model predicts a binary variable (disease region or not). Therefore, this is a classification project.
The goal here is to model the probability that a region of trees presents wilt, conditioned on the image features.
2. Data set
Data source
The dataset comprises a data matrix, where columns represent variables and rows represent instances.
The data file tree_wilt.csv contains the information for creating the model. Here, the number of variables is 6, and the number of instances is 574.
Variables
The total number of variables is 6:
- glcm: Mean gray level co-occurrence matrix (GLCM) texture index.
- green: Mean green (G) value.
- red: Mean red (R) value.
- nir: Mean near-infrared (NIR) value.
- pan_band: Standard deviation.
- class: Diseased trees or all other land covers.
Instances
The total number of instances is 574. We divide them into training, generalization, and testing subsets. The number of training instances is 346 (60%), the number of selection instances is 114 (20%), and the number of testing instances is 114 (20%).
This data represents satellite images of forest areas taken with four-channel imagery. This technique records the near-infrared frequencies, which vegetation reflects greatly for cooling purposes, as it absorbs most of the visible light as the energy source for photosynthesis.

Statistical analysis is always mandatory to detect possible issues related to the dataset. Therefore, a joint task before configuring the model is to check the data distribution. For example, the chart below shows the distribution across the sample of the instances of the green variable.
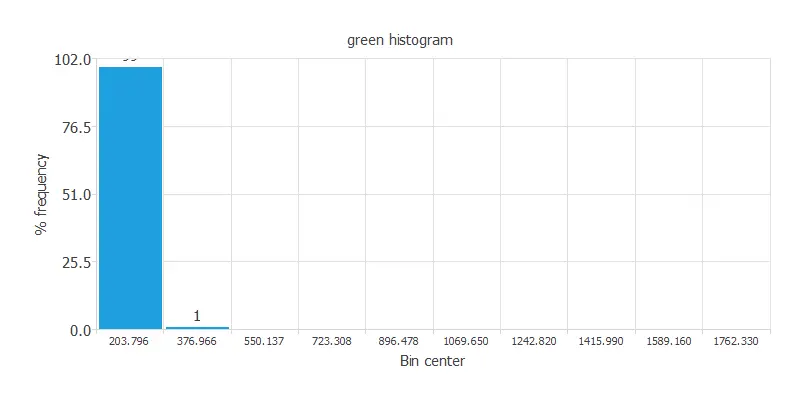
As we can see, there are outliers among our data. First, we must eliminate these instances. The following chart displays the distribution of the green variable after removing outliers from the data.
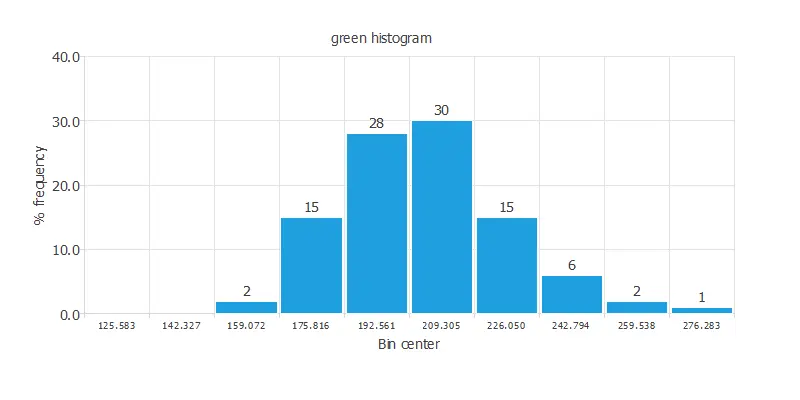
As expected, now the distribution of the green variable is correctly displayed. A uniform distribution of the data is always desired. This chart shows a normal distribution of the instances.
3. Neural network
Now we have to configure the neural network that represents the classification function.
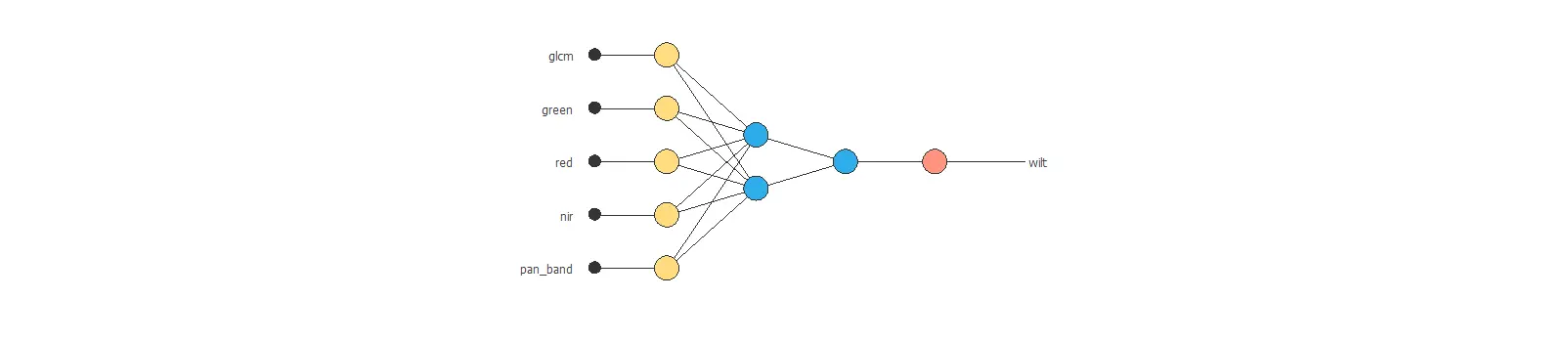
The number of inputs is 5, and the number of outputs is 1. Therefore, our neural network will comprise 5 scaling neurons and one probabilistic neuron. We will assume three hidden neurons in the perceptron layer as a first guess.
The binary probabilistic method will be applied in this case, as we have a binary classification model. Nevertheless, choosing the continuous probabilistic method would also be a correct approach.
The following picture shows a graph of the neural network for this example.
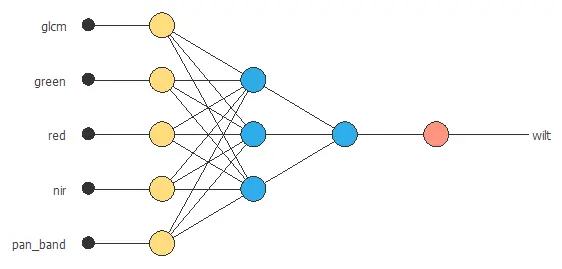
4. Training strategy
Loss index
The loss index defines the task the neural network must accomplish. The normalized squared error with strong L2 regularization is used here.
The learning problem is finding a neural network that minimizes the loss index. A neural network fits the data set (error term) without undesired oscillations (regularization term).
Optimization algorithm
The procedure used to carry out the learning process is called an optimization algorithm. The model applies the optimization algorithm to the neural network to minimize the loss as much as possible. How the neural network’s parameters are set determines the type of training.
The quasi-Newton method is used here as the optimization algorithm in the training strategy.
Training
The following chart illustrates how the training and selection errors decrease as the optimization algorithm epochs increase during the training process.
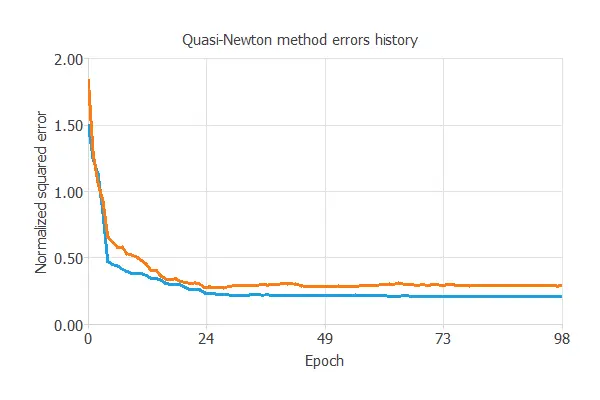
The final values are training error = 0.206 and selection error = 0.288, respectively, in terms of NSE.
5. Model selection
The objective of model selection is to find a network architecture with the best generalization properties, which minimizes the error on the selected instances of the data set.
More specifically, we aim to develop a neural network with a selection error of less than 0.288, the value we have achieved.
Order selection algorithms train several network architectures with different numbers of neurons and select the one with the smallest selection error.
The incremental order method starts with a few neurons and increases the complexity at each iteration. The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.
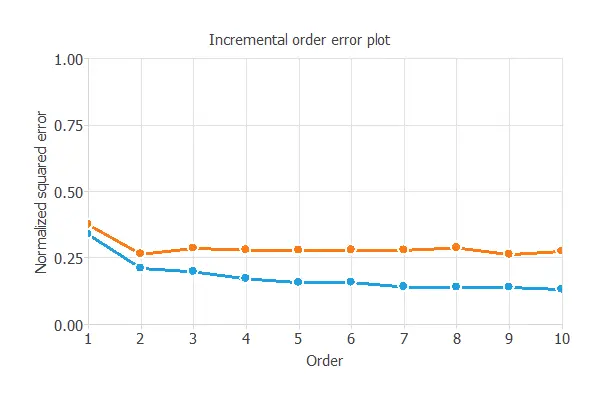
After model selection, an optimum selection error of 0.263 NSE has been found for 2 hidden neurons.
The final network architecture is displayed below.
6. Testing analysis
The last step is to test the generalization performance of the trained neural network.
Confusion matrix
The following table contains the elements of the confusion matrix for this application.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 42 (37.8%) | 5 (4.5%) |
| Real negative | 7 (6.31%) | 57 (51.4%) |
Classification metrics
The following list depicts the binary classification tests for this application:
- Accuracy: 89.2% (ratio of correctly classified samples).
- Error: 10.8% (ratio of misclassified samples).
- Sensitivity: 89.3% (percentage of actual positives classified as positive).
- Specificity: 89.1% (percentage of actual negatives classified as negative).
Therefore, we can conclude that this model has good performance.
7. Model deployment
The neural network is now ready to predict outputs for inputs it has never seen.
The model provides a specific prediction with determined values for its input variables, as shown below.
- glcm: 127.369
- green: 204.672
- red: 105.426
- nir: 447.619
- pan_band: 20.5116
The model predicts that the previous values correspond to a region of diseased trees.
References
- The data for this problem has been taken from the UCI Machine Learning Repository.
- Johnson, B., Tateishi, R., Hoan, N., 2013. A hybrid pansharpening approach and multiscale object-based image analysis for mapping diseased pine and oak trees. International Journal of Remote Sensing, 34 (20), 6969-6982.



