This example utilizes machine learning to model the energy generated as a function of exhaust vacuum and ambient variables, and leverages this model to enhance the power plant’s performance.
A combined-cycle power plant comprises gas turbines, steam turbines, and heat recovery steam generators.
In this type of plant, electricity is generated by combining gas and steam turbines in a single cycle.
Then, it is transferred from one turbine to another.
The ambient variables affect the gas turbine performance, while the vacuum is collected and affects the steam turbine.
We use the explainable machine learning platform Neural Designer to build this model. You can use the free trial to follow the process step by step.
Contents
1. Application type
This is an approximation project since the variable we want to predict is continuous (energy production).
The primary goal is to model energy production as a function of environmental and control variables.
2. Data set
The data set contains three concepts:
- Data source.
- Variables.
- Instances.
Data source
The file combined_cycle_power_plant.csv has 9,568 samples with five variables, recorded every second over six years of full-load operation.
Variables
The variables, or features, are the following:
Environmental Conditions
- Ambient temperature (°C): Surrounding air temperature.
- Ambient pressure (mbar): Atmospheric pressure at the plant site.
- Relative humidity (%): Moisture content in the air.
Operational Conditions
Exhaust vacuum (cm Hg): Vacuum level at the plant’s condenser.
Target Variable
Energy output (MW): Net hourly electrical energy generated by the plant.
Instances
The instances are divided into training, selection, and testing subsets. They represent 60%, 20%, and 20% of the original instances, respectively, and are randomly split.
Distributions
Calculating the data distributions helps us verify the accuracy of the available information and detect anomalies.
The following chart shows the histogram for the variable energy_output.
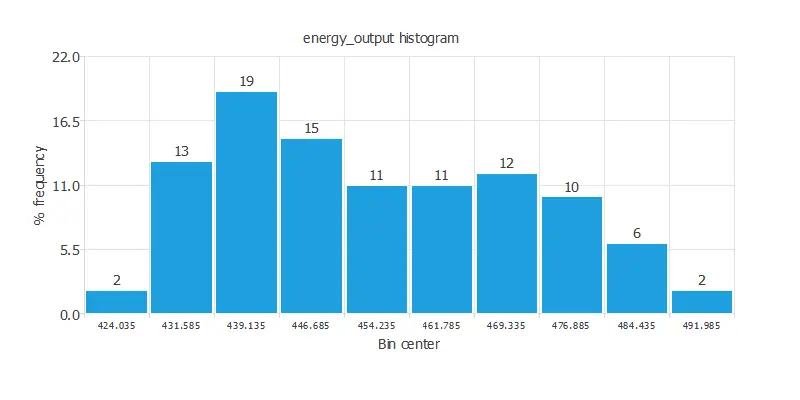
As we can see, there are more scenarios where the energy produced is small than where it is significant.
Input-target correlations
It is also interesting to look for dependencies between a single input and a single target variable.
To do that, we can plot an input-target correlation chart.
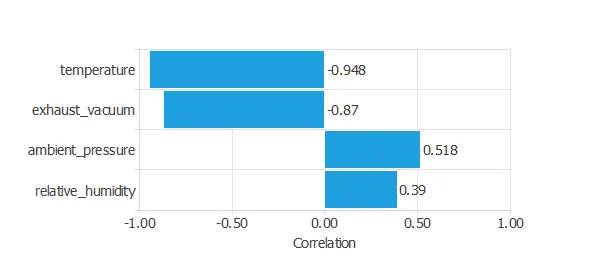
The temperature yields the highest correlation (generally, the higher the temperature, the less energy production).
Scatter charts
Next, we plot a scatter chart for the energy output and the exhaust vacuum.
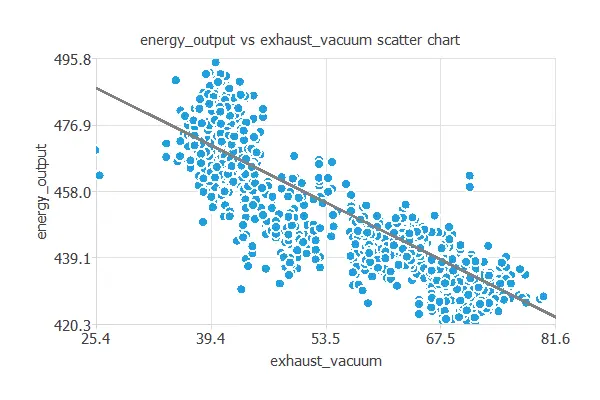
As we can see, the energy output is highly correlated with the exhaust vacuum. In general, the more exhaust vacuum, the less energy production.
3. Neural network
The second step is to build a neural network that represents the approximation function.
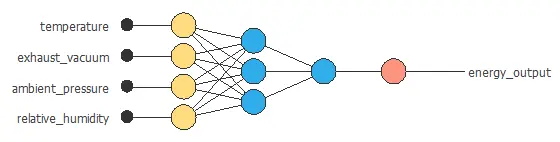
The neural network has four inputs (temperature, exhaust vacuum, ambient pressure, and relative humidity) and one output (energy output).
Approximation models usually contain the following layers:
- Scaling layer.
- Perceptron layers.
- Unscaling layer.
Scaling layer
The scaling layer contains the statistics of the inputs.
We use the mean and standard deviation scaling method as all inputs have normal distributions.
Dense layers
We use 2 perceptron layers here:
- The first perceptron layer has 4 inputs, 3 neurons, and a hyperbolic tangent activation function.
- The second perceptron layer has 3 inputs, 1 neuron, and a linear activation function.
Unscaling layer
The unscaling layer contains the statistics of the outputs.
As the output has a normal distribution, we use the mean and standard deviation unscaling method.
Neural network graph
The following graph represents the neural network for this example.
4. Training strategy
The fourth step is to select an appropriate training strategy. It is composed of two things:
- A loss index.
- An optimization algorithm.
Loss index
The loss index defines what the neural network will learn. It is composed of an error term and a regularization term.
The chosen error term is the normalized squared error.
It divides the squared difference between the network’s outputs and the dataset’s targets by a normalization factor.
A value of 1 means the network only predicts the mean, while 0 means perfect prediction.
The regularization term is the L2 regularization.
It is applied to control the complexity of the neural network by reducing the values of its parameters.
Optimization algorithm
The optimization algorithm is responsible for searching for the neural network parameters that minimize the loss index.
Here, we chose the quasi-Newton method as the optimization algorithm.
Training process
The following chart illustrates how the training (blue) and selection (orange) errors decrease with the number of epochs during the training process.
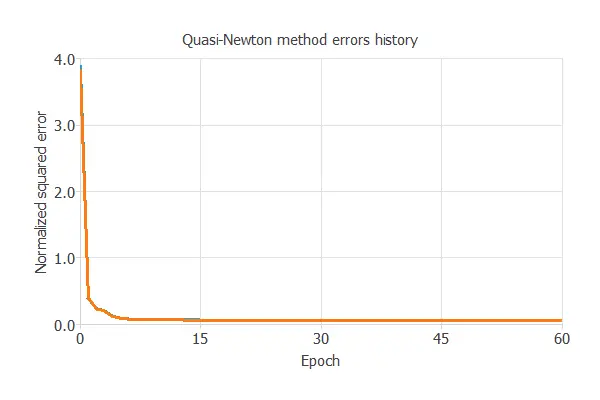
The final values are a training error of 0.057 NSE and a selection error of 0.067 NSE, respectively.
5. Model selection
Model selection algorithms enhance the generalization performance of neural networks.
The selection error we achieved is minimal (0.067 NSE), making this algorithm unnecessary.
6. Testing analysis
The purpose of the testing analysis is to validate the generalization capabilities of the neural network.
We use the testing instances in the data set, which have never been used before.
Goodnes-of-fit
A standard testing method in approximation applications is to perform a linear regression analysis between the predicted and the real energy output values.
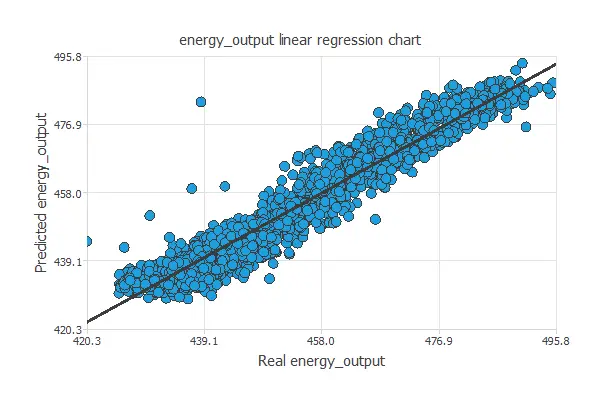
A perfect fit has a correlation coefficient R2=1.
Since our model achieves R2=0.968, the neural network predicts the testing data very well.
7. Model deployment
In the model deployment phase, the neural network predicts outputs for inputs it has not seen before.
Neural network outputs
We can calculate the neural network outputs for a given set of inputs:
- temperature: 19 degrees Celsius.
- exhaust_vacuum: 54 cm Hg.
- ambient_pressure: 1013 millibar.
- relative_humidity: 73 %.
The predicted output for these input values is the following:
- energy_output: 452 MW.
Response optimization
The objective of the Response Optimization algorithm is to utilize the mathematical model to identify optimal operating conditions. Indeed, the predictive model enables us to simulate various operating scenarios and adjust the control variables to enhance efficiency.
An example is minimizing exhaust vacuum while maintaining energy at or above the desired value.
The following table summarizes the conditions for this problem.
| Variable name | Condition | |
|---|---|---|
| Temperature | None | |
| Exhaust vacuum | Minimize | |
| Ambient pressure | None | |
| Relative humidity | None | |
| Energy | Greater than or equal to | 450 |
The next list shows the optimum values for the previous conditions.
- temperature: 19.3846 Celsius degrees.
- exhaust_vacuum: 25.432 cm Hg.
- ambient_pressure: 1021.4 millibar.
- relative_humidity: 60.8 %.
- energy: 462.086 MW.
Directional outputs
Directional outputs plot the neural network outputs through some reference points.
The next list shows the reference points for the plots.
- temperature: 19 degrees Celsius.
- exhaust_vacuum: 54 cm Hg.
- ambient_pressure: 1013 millibar.
- relative_humidity: 73 %.
Next, we define a reference point and see how the energy production varies with the exhaust vacuum around that point.
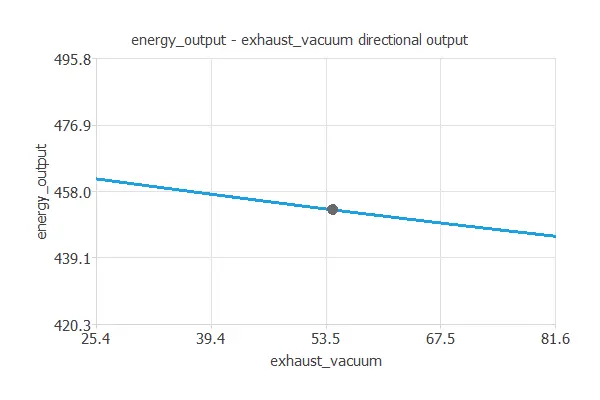
As we can see, reducing the exhaust vacuum increases energy output.
Mathematical expression
The mathematical expression represented by the predictive model is listed next:
scaled_temperature = (temperature-19.6512)/7.45247;
scaled_exhaust_vacuum = 2*(exhaust_vacuum-25.36)/(81.56-25.36)-1;
scaled_ambient_pressure = (ambient_pressure-1013.26)/5.93878;
scaled_relative_humidity = (relative_humidity-73.309)/14.6003;
y_1_1 = tanh(-0.158471 + (scaled_temperature*0.200864) + (scaled_exhaust_vacuum*0.73313)
+ (scaled_ambient_pressure*-0.19189) + (scaled_relative_humidity*0.0133642));
y_1_2 = tanh(-0.290828 + (scaled_temperature*-0.020375) + (scaled_exhaust_vacuum*-0.263848)
+ (scaled_ambient_pressure*-0.227397)+ (scaled_relative_humidity*0.337468));
y_1_3 = tanh(0.574054 + (scaled_temperature*0.572764) + (scaled_exhaust_vacuum*-0.0264721)
+ (scaled_ambient_pressure*0.109944)+ (scaled_relative_humidity*0.00934301));
scaled_energy_output = (0.162012+ (y_1_1*-0.382654) + (y_1_2*-0.126065) + (y_1_3*-0.748958));
energy_output = (0.5*(scaled_energy_output+1.0)*(495.76-420.26)+420.26);8. Tutorial video
You can watch the step-by-step tutorial video below to help you complete this Machine Learning example
for free using the easy-to-use machine learning software Neural Designer.
References
- Pinar Tufekci, Prediction of full load electrical power output of a baseload operated combined cycle power plant using machine learning methods, International Journal of Electrical Power & Energy Systems, Volume 60, September 2014, Pages 126-140, ISSN 0142-0615.
- Heysem Kaya, Pinar Tufekci, Fikret S. Gurgen: Local and Global Learning Methods for Predicting Power of a Combined Gas & Steam Turbine, Proceedings of the International Conference on Emerging Trends in Computer and Electronics Engineering ICETCEE 2012, pp. 13-18 (Mar. 2012, Dubai).



