This example is solved with Neural Designer. You can use the free trial to understand how the solution is achieved step by step.

Contents

1. Application type.
2. Data set.
3. Neural network.
4. Training strategy.
5. Model selection.
6. Testing analysis.
7. Model deployment.

1. Application type

2. Data set

The first step is to prepare the data set, which is the source of information for the approximation problem.

• distance_to_solar_noon, in radians.
• temperature, daily average temperature, in degrees Celsius.
• wind_direction, daily average wind direction, in degrees (0-360).
• wind_speed, daily average wind speed, in meters per second.
• sky_cover, on a five-step scale from 0 to 4, with 0 completely clear and 4 wholly covered.
• visibility, in kilometers.
• humidity, in percentage.
• average_wind_speed, average wind speed during the 3 hours de measure was taken in meters per second.
• average_pressure, average barometric pressure during the 3 hours the measure was taken in, in mercury inches.
• power_generated, in Jules for each 3 hours.

Our target variable will be the last one, power-generated.

The instances are divided into training, selection, and testing subsets. They represent 60%, 20%, and 20% of the original instances, respectively, and are randomly split.

Calculating the data distributions helps us check for the correctness of the available information and detect anomalies.
The following chart shows the histogram for the power-generated variable:

It is also interesting to look for dependencies between a single input and single target variables. To do that, we can plot an inputs-targets correlations chart.

In this case, the highest correlation is with the distance to solar noon (the solar plant generates the closer to solar noon, the more power).

Next, we plot a scatter chart for the most significant correlations for our target variable.

3. Neural network

The second step is building a neural network representing the approximation function. Approximation models usually contain the following layers:

• Scaling layer.
• Perceptron layers.
• Unscaling layer.

The neural network has nine inputs (distance to solar noon, temperature, wind direction, wind speed, sky cover, visibility, humidity, average wind speed (period), and average pressure (period)) and one output (power generated).

The scaling layer contains the statistics of the inputs. We use the automatic setting for this layer to accommodate the best scaling technique for our data.

We use 2 perceptron layers here:

• The first perceptron layer has 9 inputs, 3 neurons, and a hyperbolic tangent activation function.
• The second perceptron layer has 3 inputs, 1 neuron, and a linear activation function.

The unscaling layer contains the statistics of the outputs. We use the automatic method as before.

The following graph represents the neural network for this example.

4. Training strategy

The fourth step is to select an appropriate training strategy. It is composed of two parameters:

• Loss index.
• Optimization algorithm.

The loss index defines what the neural network will learn. It is composed of an error term and a regularization term.

The error term we choose is the normalized squared error. It divides the squared error between the neural network outputs and the data set’s targets by its normalization coefficient. If the normalized squared error is 1, the neural network predicts the data ‘in the mean’, while zero means a perfect data prediction. This error term does not have any parameters to set.

The regularization term is the L2 regularization. It controls the neural network’s complexity by reducing the parameters’ value. We use a weak weight for this regularization term.

The optimization algorithm is in charge of searching for the neural network parameters that minimize the loss index. Here, we chose the quasi-Newton method as an optimization algorithm.

The following chart shows how the training (blue) and selection (orange) errors decrease with the epochs during the training process. The final values are training error = 0.121 NSE and selection error = 0.122 NSE, respectively.

5. Model selection

The objective of model selection is to find the network architecture with the best generalization properties. We want to improve the final selection error obtained before (0.122 NSE).

The best selection error is achieved using a model with the most appropriate complexity to produce a good data fit. Order selection algorithms are responsible for finding the optimal number of perceptrons in the neural network.

The following chart shows the results of the incremental order algorithm. The blue line plots the final training error as a function of the number of neurons. The orange line plots the final selection error as a function of the number of neurons.

As we can see, the final training error continuously decreases with the number of neurons. However, the final selection error takes a minimum value at some point. The optimal number of neurons is 8, corresponding to a selection error of 0.089 NSE.

The following figure shows the optimal network architecture for this application.

6. Testing analysis

The purpose of the testing analysis is to validate the generalization capabilities of the neural network. We use the testing instances in the data set, which have never been used before.

A standard testing method in approximation applications is to perform a linear regression analysis between the predicted and the real pollutant level values.

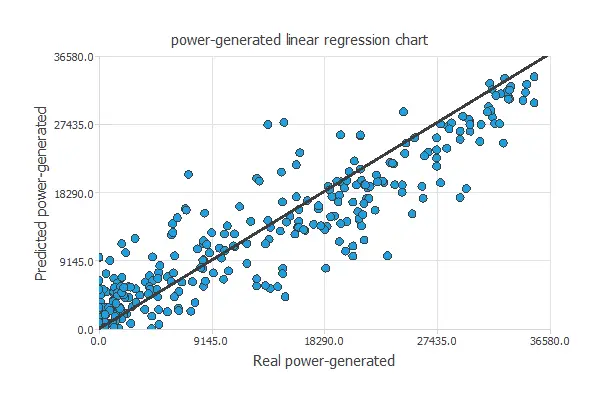
For a perfect fit, the correlation coefficient R2 would be 1. As we have R2 = 0.951, the neural network predicts the testing data quite well.

7. Model deployment

In the model deployment phase, the neural network predicts outputs for inputs it has never seen.

We can calculate the neural network outputs for a given set of inputs:

• distance_to_solar_noon: 0.503 radians.
• temperature: 58.468ºC.
• wind_direction: 24.953º.
• wind_speed: 10.097 m/s.
• sky_cover: 1.988 over 4.
• visibility: 9.558 km.
• humidity: 73.524%.
• average-wind-speed-(period): 10.136 m/s.
• average_pressure_(period): 30.062 mercury inches.

The predicted output for these input values is the following:

• power_generated: 3012.461 Jules per 3-hour period.

Directional outputs plot the neural network outputs through some reference points.

The next list shows the reference point for the plots.

• distance_to_solar_noon: 0.503 radians.
• temperature: 58.468ºC.
• wind_direction: 24.953º.
• wind_speed: 10.097 m/s.
• sky_cover: 1.988 over 4.
• visibility: 9.558 km.
• humidity: 73.524%.
• average_wind_speed: 10.136 m/s.
• average_pressure: 30.062 mercury inches.

We can see here how the distance to solar noon affects the power generated:

The mathematical expression represented by the predictive model is displayed next:

scaled_distance-to-solar-noon = distance-to-solar-noon*(1+1)/(1.141360044-(0.05040090159))-0.05040090159*(1+1)/(1.141360044-0.05040090159)-1;
scaled_temperature = temperature*(1+1)/(78-(42))-42*(1+1)/(78-42)-1;
scaled_wind-direction = wind-direction*(1+1)/(36-(1))-1*(1+1)/(36-1)-1;
scaled_wind-speed = wind-speed*(1+1)/(26.60000038-(1.100000024))-1.100000024*(1+1)/(26.60000038-1.100000024)-1;
scaled_sky-cover = sky-cover*(1+1)/(4-(0))-0*(1+1)/(4-0)-1;
scaled_visibility = visibility*(1+1)/(10-(0))-0*(1+1)/(10-0)-1;
scaled_humidity = humidity*(1+1)/(100-(14))-14*(1+1)/(100-14)-1;
scaled_average-wind-speed-(period) = average-wind-speed-(period)*(1+1)/(40-(0))-0*(1+1)/(40-0)-1;
scaled_average-pressure-(period) = average-pressure-(period)*(1+1)/(30.53000069-(29.47999954))-29.47999954*(1+1)/(30.53000069-29.47999954)-1;
perceptron_layer_0_output_0 = tanh[ -0.176941 + (scaled_distance-to-solar-noon*0.899353)+ (scaled_temperature*-0.620422)+ (scaled_wind-direction*0.136902)+ (scaled_wind-speed*0.836426)+ (scaled_sky-cover*0.12677)+ (scaled_visibility*0.177673)+ (scaled_humidity*0.99292)+ (scaled_average-wind-speed-(period)*0.443054)+ (scaled_average-pressure-(period)*-0.994507) ];
perceptron_layer_0_output_1 = tanh[ -0.290833 + (scaled_distance-to-solar-noon*-0.221985)+ (scaled_temperature*-0.513855)+ (scaled_wind-direction*-0.931396)+ (scaled_wind-speed*0.848389)+ (scaled_sky-cover*0.985168)+ (scaled_visibility*-0.0263062)+ (scaled_humidity*0.330078)+ (scaled_average-wind-speed-(period)*-0.260864)+ (scaled_average-pressure-(period)*-0.255554) ];
perceptron_layer_0_output_2 = tanh[ 0.400513 + (scaled_distance-to-solar-noon*-0.969666)+ (scaled_temperature*0.269836)+ (scaled_wind-direction*-0.749023)+ (scaled_wind-speed*-0.764648)+ (scaled_sky-cover*0.419434)+ (scaled_visibility*0.692505)+ (scaled_humidity*-0.314514)+ (scaled_average-wind-speed-(period)*0.405884)+ (scaled_average-pressure-(period)*0.739563) ];
perceptron_layer_0_output_3 = tanh[ 0.624329 + (scaled_distance-to-solar-noon*0.475281)+ (scaled_temperature*-0.607056)+ (scaled_wind-direction*0.260742)+ (scaled_wind-speed*-0.190369)+ (scaled_sky-cover*0.662354)+ (scaled_visibility*0.73761)+ (scaled_humidity*0.216064)+ (scaled_average-wind-speed-(period)*0.854614)+ (scaled_average-pressure-(period)*0.157959) ];
perceptron_layer_0_output_4 = tanh[ 0.019043 + (scaled_distance-to-solar-noon*0.269653)+ (scaled_temperature*-0.166748)+ (scaled_wind-direction*0.554626)+ (scaled_wind-speed*-0.171143)+ (scaled_sky-cover*-0.333191)+ (scaled_visibility*0.243896)+ (scaled_humidity*0.0197754)+ (scaled_average-wind-speed-(period)*-0.169983)+ (scaled_average-pressure-(period)*-0.991638) ];
perceptron_layer_0_output_5 = tanh[ -0.243835 + (scaled_distance-to-solar-noon*0.578796)+ (scaled_temperature*0.753418)+ (scaled_wind-direction*-0.0349121)+ (scaled_wind-speed*0.94281)+ (scaled_sky-cover*-0.286865)+ (scaled_visibility*0.665833)+ (scaled_humidity*-0.105347)+ (scaled_average-wind-speed-(period)*-0.686279)+ (scaled_average-pressure-(period)*0.641052) ];
perceptron_layer_0_output_6 = tanh[ -0.579224 + (scaled_distance-to-solar-noon*0.20166)+ (scaled_temperature*-0.9953)+ (scaled_wind-direction*0.804138)+ (scaled_wind-speed*-0.209045)+ (scaled_sky-cover*-0.3573)+ (scaled_visibility*0.747437)+ (scaled_humidity*-0.83667)+ (scaled_average-wind-speed-(period)*0.595459)+ (scaled_average-pressure-(period)*-0.350708) ];
perceptron_layer_0_output_7 = tanh[ 0.880127 + (scaled_distance-to-solar-noon*-0.731995)+ (scaled_temperature*0.578369)+ (scaled_wind-direction*-0.372803)+ (scaled_wind-speed*0.102295)+ (scaled_sky-cover*-0.872192)+ (scaled_visibility*-0.247559)+ (scaled_humidity*0.613586)+ (scaled_average-wind-speed-(period)*-0.691589)+ (scaled_average-pressure-(period)*-0.0609741) ];
perceptron_layer_1_output_0 = [ -0.747375 + (perceptron_layer_0_output_0*0.643494)+ (perceptron_layer_0_output_1*0.631348)+ (perceptron_layer_0_output_2*0.720947)+ (perceptron_layer_0_output_3*-0.310059)+ (perceptron_layer_0_output_4*-0.123047)+ (perceptron_layer_0_output_5*0.611084)+ (perceptron_layer_0_output_6*-0.208069)+ (perceptron_layer_0_output_7*-0.706238) ];
unscaling_layer_output_0 = perceptron_layer_1_output_0*(36580-0)/(1+1)+0+1*(36580-0)/(1+1);

8. Video tutorial

You can watch the step-by-step tutorial video below to help you complete this machine learning example for free using the software Neural Designer.

Ph.D. candidate Alexandra Constantin compiled the data.

Related posts