Predict customer churn in a telecommunications company using machine learning

Customer churn is a big problem for telecommunications companies.
Indeed, their annual churn rates are usually higher than 10%.

Telecommunications

For that reason, they develop strategies to keep as many clients as possible.

This example uses machine learning to predict which customers will leave the company, take measures, and prevent it.

Contents:

1. Application type.
2. Data set.
3. Neural network.
4. Training strategy.
5. Model selection.
6. Testing analysis.
7. Model deployment.

This example is solved with Neural Designer.
To follow it step by step, you can use the free trial.

1. Application type

This is a classification project since the variable to be predicted is binary (churn or loyal customer).

The goal here is to model churn probability, conditioned on the customer features.

2. Data set

The data file telecommunications_churn.csv contains a total of 19 features for 3333 customers.
Each row corresponds to a client of a telecommunications company for whom it has been collected information about the type of plan they have contracted, the minutes they have talked, or the charge they pay every month.

The data set includes the following variables:

• account_length
• voice_mail_plan
• voice_mail_messages
• day_mins
• evening_mins
• night_mins
• international_mins
• customer_service_calls
• international_plan
• day_calls
• day_charge
• evening_calls
• evening_charge
• night_calls
• night_charge
• international_calls
• international_charge
• total_charge
• churn: This is the target variable. It is the one that determines whether the client is still in the company or not.

The first step of this analysis is to check the distributions of the variables.
The next figure shows a pie chart of churn and loyal customers.

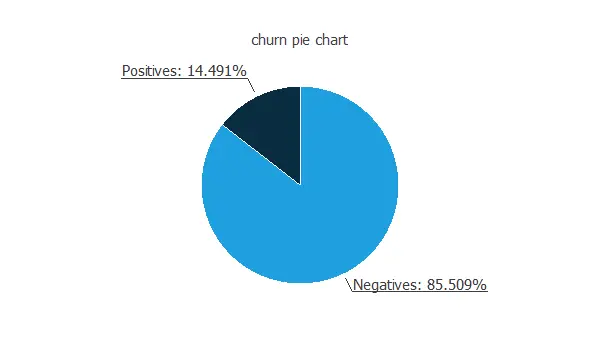
As we can see, the annual churn rate in this company is almost 15%.
Also, we observe that the dataset is unbalanced.

The inputs-targets correlations might indicate to us what factors are most influential for the churn of customers.

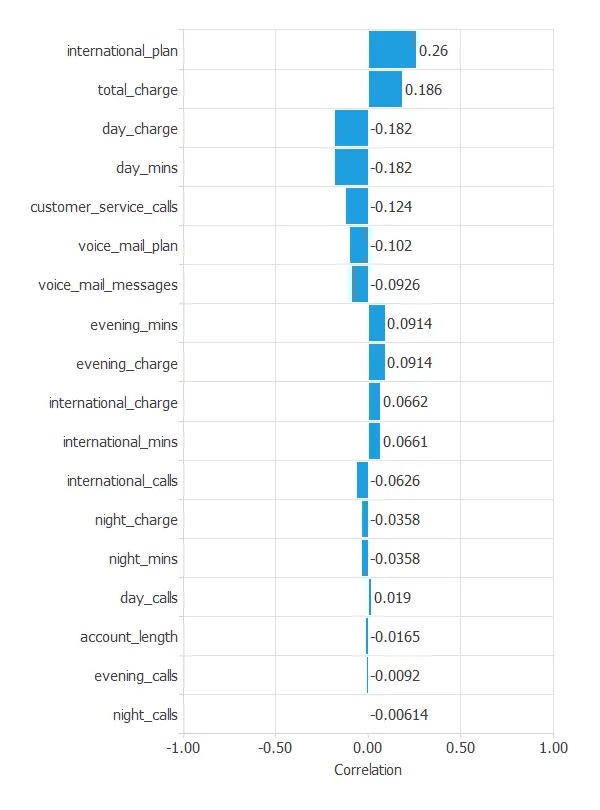
Here, the most correlated variable with churn is international_plan.
A positive correlation here means that a high ratio of customers with an international plan leaves the company.

2. Neural network

The second step is to choose a neural network to represent the classification function.
For classification problems, it is composed of:

• A scaling layer.
• Two perceptron layers.
• A probabilistic layer.

For the scaling layer,
the mean and standard deviation scaling method is set.

We set 2 perceptron layers, one hidden layer with 3 neurons as a first guess and one output layer
with 1 neuron, both layers having the logistic activation function.

At last, we will set the continuous probabilistic method for the probabilistic layer.

The architecture shown below consists of 18 scaling neurons (yellow), five neurons in the first layer (blue), and one probabilistic neuron (red).

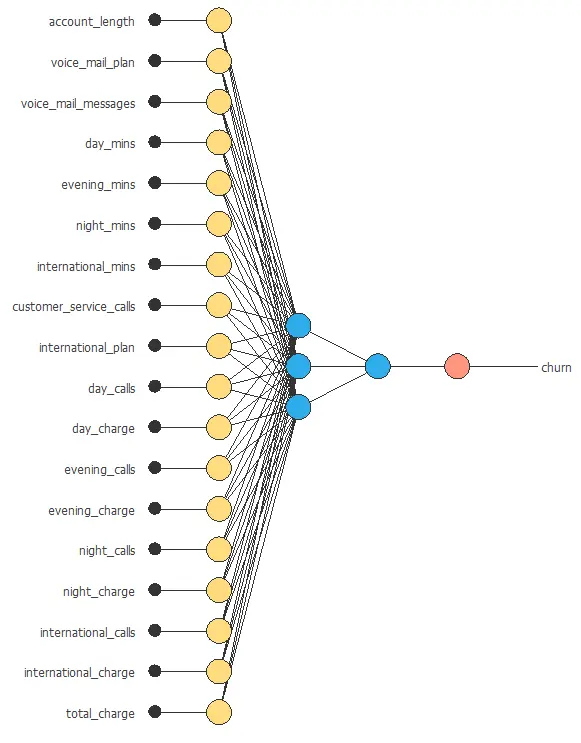
4. Training strategy

The next step is to select an appropriate training strategy, which defines what the neural network will learn.
A general training strategy is composed of two concepts:

• A loss index.
• An optimization algorithm.

As we saw before, the data set is unbalanced.
In that way, we set the weighted squared error

The following chart shows how the loss decreases during the training process with the iterations of the Quasi-Newton method.

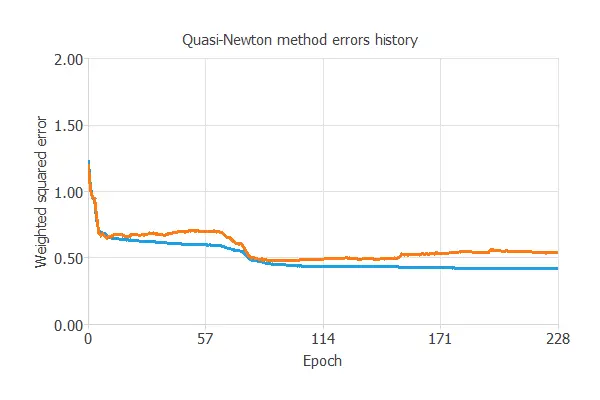
As we can see, the final training and selection errors are
training error = 0.384 WSE and selection error = 0.455 WSE, respectively.

5. Model selection

The objective of model selection is to find the network architecture with the best generalization properties,
that is, that which minimizes the error on the selected instances of the data set.

We want to find a neural network with a selection error of less than 0.455 WSE,
which is the value we have achieved so far.

Order selection algorithms train several network architectures with a different number of neurons
and select that with the smallest selection error.

The incremental order method starts with a small number of neurons and increases the complexity at each iteration.
The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.

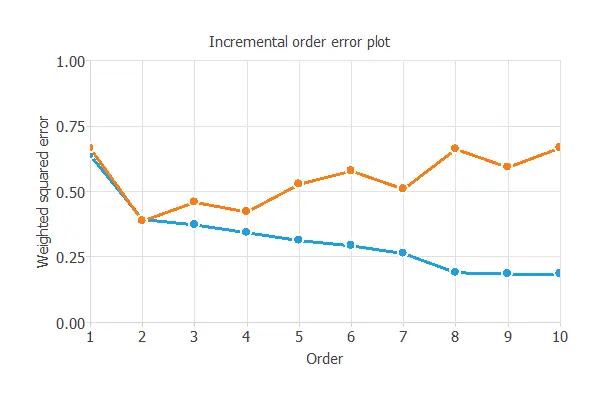
As we can see, the optimal number of perceptrons in the first layer is optimal order = 2,
and the optimum error on the selected instances is selection error = 0.455 WSE.

6. Testing analysis

The purpose of the testing analysis is to evaluate the performance of the trained model on new data that have been used neither for training nor for selection.
For that, we use the testing instances.

The ROC curve measures the discrimination capacity of the classifier between positives and negatives instances.
The next chart shows the ROC curve of our problem.

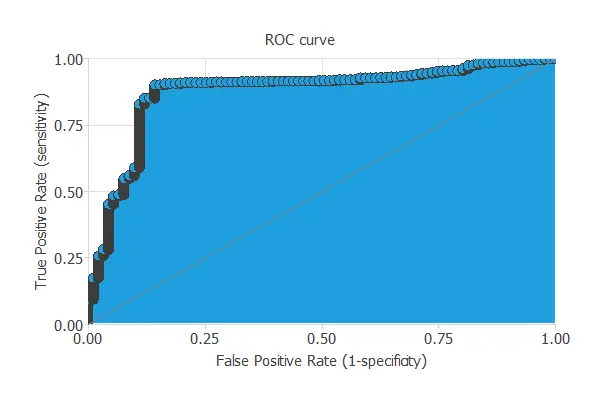
The proximity of the curve to the upper left corner means that the model has an excellent capacity to discriminate between the two classes.

The most important parameter from the ROC curve is the area under the curve (AUC).
This value is 0.5 for a random classifier and 1 for a perfect classifier.
For this example, we have AUC = 0.896, which means that the model is well predicting our customers’ churn.

confusion matrix

The binary classification tests are calculated from the values of the confusion matrix.

• Classification accuracy: 91.2% (ratio of correctly classified samples).
• Error rate: 8.8% (ratio of misclassified samples).
• Sensitivity: 76.9% (percentage of actual positive classified as positive).
• Specificity: 93.9% (percentage of actual negative classified as negative).

These binary classification tests show that the model can correctly predict most of the instances.

7. Model deployment

In the model deployment phase, the neural network can be used to predict outputs for inputs that it has never seen.

We can calculate the neural network outputs for a given set of inputs:

• account_length: 101.065.
• voice_mail_plan: 1.
• voice_mail_messages: 8.09901.
• day_mins: 179.775.
• evening_mins: 200.98.
• night_mins: 200.871.
• international_mins: 10.2373.
• customer_service_calls: 1.56286.
• international_plan: 0.
• day_calls: 100.436.
• day_charge: 30.5623.
• evening_calls: 100.114.
• evening_charge: 17.0835.
• night_calls: 100.108.
• night_charge: 9.03933.
• international_calls: 4.47945.
• international_charge: 2.76457.
• total_charge: 59.4498.

The predicted churn for these inputs is the following:

• churn: 0.047950.

We can export the mathematical expression of the neural network for future use
to any bank software used for this purpose.
This expression is listed below.

scaled_account_length = (account_length-101.065)/39.8221;
scaled_voice_mail_plan = (voice_mail_plan-0.276628)/0.447398;
scaled_voice_mail_messages = (voice_mail_messages-8.09901)/13.6884;
scaled_day_mins = (day_mins-179.775)/54.4674;
scaled_evening_mins = (evening_mins-200.98)/50.7138;
scaled_night_mins = (night_mins-200.872)/50.5738;
scaled_international_mins = (international_mins-10.2373)/2.79184;
scaled_customer_service_calls = (customer_service_calls-1.56286)/1.31549;
scaled_international_plan = (international_plan-0.0969097)/0.295879;
scaled_day_calls = (day_calls-100.436)/20.0691;
scaled_day_charge = (day_charge-30.5623)/9.25943;
scaled_evening_calls = (evening_calls-100.114)/19.9226;
scaled_evening_charge = (evening_charge-17.0835)/4.31067;
scaled_night_calls = (night_calls-100.108)/19.5686;
scaled_night_charge = (night_charge-9.03932)/2.27587;
scaled_international_calls = (international_calls-4.47945)/2.46121;
scaled_international_charge = (international_charge-2.76458)/0.753773;
scaled_total_charge = (total_charge-59.4498)/10.5023;
y_1_1 = Logistic (-10.0534+ (scaled_account_length*0.837489)+ (scaled_voice_mail_plan*-1.92865)+ (scaled_voice_mail_messages*2.43032)+ (scaled_day_mins*0.619668)+ (scaled_evening_mins*-0.822147)+ (scaled_night_mins*-0.0592015)+ (scaled_international_mins*-0.331996)+ (scaled_customer_service_calls*5.14956)+ (scaled_international_plan*-0.486517)+ (scaled_day_calls*0.247419)+ (scaled_day_charge*-0.844425)+ (scaled_evening_calls*-0.385092)+ (scaled_evening_charge*-0.0288761)+ (scaled_night_calls*0.351411)+ (scaled_night_charge*0.330832)+ (scaled_international_calls*-0.244305)+ (scaled_international_charge*0.175898)+ (scaled_total_charge*-1.06894));
y_1_2 = Logistic (-10.4815+ (scaled_account_length*-0.143055)+ (scaled_voice_mail_plan*-3.90343)+ (scaled_voice_mail_messages*-1.00465)+ (scaled_day_mins*2.01689)+ (scaled_evening_mins*0.674122)+ (scaled_night_mins*1.06811)+ (scaled_international_mins*1.02216)+ (scaled_customer_service_calls*-0.474987)+ (scaled_international_plan*8.85213)+ (scaled_day_calls*-0.106802)+ (scaled_day_charge*2.69922)+ (scaled_evening_calls*-0.0539915)+ (scaled_evening_charge*1.90287)+ (scaled_night_calls*-0.301365)+ (scaled_night_charge*0.201187)+ (scaled_international_calls*0.227339)+ (scaled_international_charge*-0.658305)+ (scaled_total_charge*2.57132));
non_probabilistic_churn = Logistic (-2.085+ (y_1_1*5.50847)+ (y_1_2*4.52172));
churn = probability(non_probabilistic_churn);

logistic(x){
   return 1/(1+exp(-x))
}

probability(x){
   if x < 0
       return 0
   else if x > 1
       return 1
   else
       return x
}
    

Related posts:

• Predict churn of customers in a bank.
• Churn prevention.