This example builds a machine learning model to evaluate the radiation efficiency of patch antennas with different features. We used data from 8 antennas, including variables extracted from their geometries.
A patch antenna is a wireless antenna that uses a flat, rectangular metal patch on a substrate to transmit or receive radio frequency (RF) signals. The coefficient of reflection, S11, measures the power reflected to the source when RF signals are transmitted through the patch antenna. S11 is typically expressed as a ratio of power, with values close to 0 indicating tiny reflection and values close to 1 indicating significant reflection.
The predicted variable in this application is the coefficient of reflection, S11, for a patch antenna. Therefore, this is an approximation project.Optimizing the antenna design aims to achieve the lowest possible value for S11, signifying high power transmission and minimal reflection levels, employing artificial intelligence and machine learning.
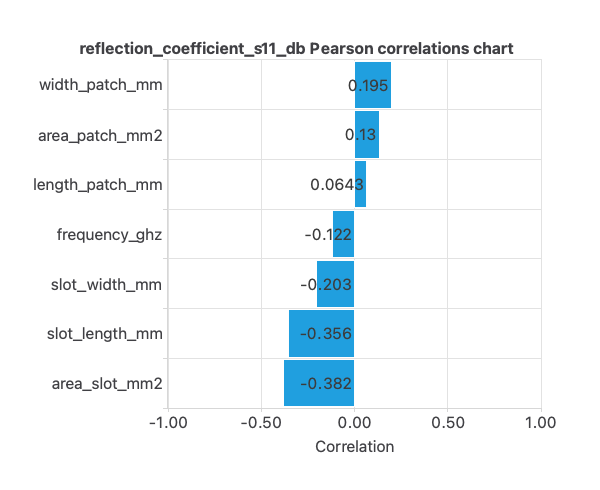 Here, the most correlated variables with survival status are area_slot_mm2 and slot_length_mm.
Here, the most correlated variables with survival status are area_slot_mm2 and slot_length_mm.
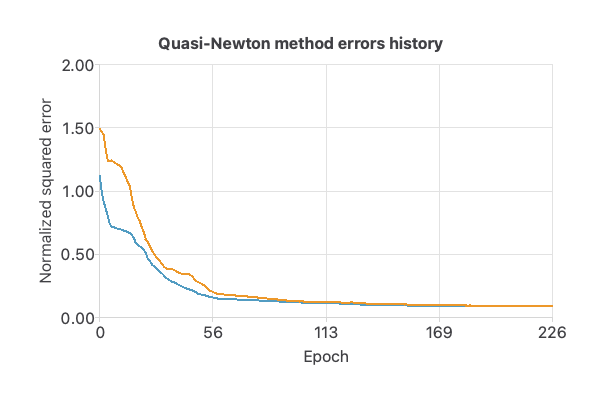 As we can see in the previous image, the curves have converged.
As we can see in the previous image, the curves have converged.
 As we can see, the average error is around 1%.
Additionally, the errors histogram shows the distribution of the errors from the neural network on the testing samples. In general, we expect a normal distribution like this.
As we can see, the average error is around 1%.
Additionally, the errors histogram shows the distribution of the errors from the neural network on the testing samples. In general, we expect a normal distribution like this.
 As we can observe, most of the errors are around 0.
As we can observe, most of the errors are around 0.
Contents
This dataset was generated using HFSS software, and the radiation frequency was kept at 2.4 GHz, commonly used for Bluetooth and WLAN operations, and can be used to optimize the design and performance of patch antennas.1. Application type
2. Data set
This dataset features information on patch antennas, a type of microstrip antenna widely used in wireless communications. The dataset includes various dimensions and parameters of the antenna, including the operating frequency, dimensions of the patch and slots, and a measure of the antenna’s reflection coefficient. The data is organized in clusters; there are 8 clusters in total. The number of input variables, or attributes for each sample, is 7. The target variable is S11. The following list summarizes the variables information:- frequency_ghz: The operating frequency of the antenna, measured in gigahertz.
- length_patch_mm: The length of the patch antenna, measured in millimeters.
- width_patch_mm: The width of the patch antenna, measured in millimeters.
- area_patch_mm2: The total area of the patch antenna, measured in square millimeters.
- slot_length_mm: The length of the slots on the antenna, measured in millimeters.
- slot_width_mm: The width of the slots on the antenna, measured in millimeters.
- area_slot_mm2: The total area of the slots on the antenna, measured in square millimeters.
- reflection_coefficient_s11_db: The S11 parameter, measured in decibels, measures the antenna’s reflection coefficient.
 Here, the most correlated variables with survival status are area_slot_mm2 and slot_length_mm.
Here, the most correlated variables with survival status are area_slot_mm2 and slot_length_mm.
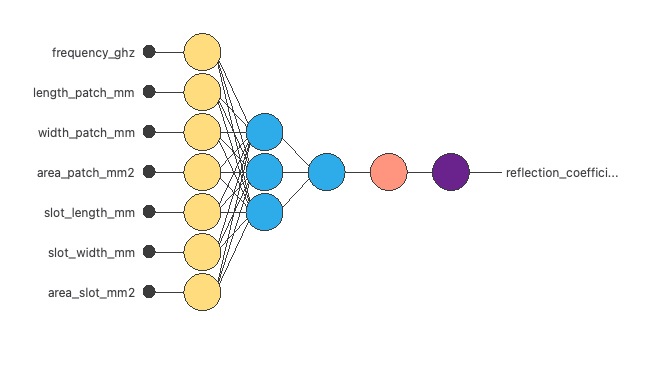
3. Neural network
The next step is to set a neural network representing the approximation function. For this class of applications, the neural network consists of the following components: The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables. Here, the minimum-maximum method has been set. As we use 7 input variables, the scaling layer has 7 inputs. We use 2 perceptron layers here:- The first perceptron layer has 7 inputs, 3 neurons, and a hyperbolic tangent activation function
- The second perceptron layer has 3 inputs, 1 neuron, and a linear activation function

4. Training strategy
The fourth step is to set the training strategy, which is composed of two terms:- A loss index.
- An optimization algorithm.
 As we can see in the previous image, the curves have converged.
As we can see in the previous image, the curves have converged.
5. Testing analysis
The testing analysis aims to validate the performance of the generalization properties of the trained neural network. In this case, we show the minimums, maximums, mean, and standard deviations of the absolute and percent errors of the neural network for the testing data. As we can see, the average error is around 1%.
Additionally, the errors histogram shows the distribution of the errors from the neural network on the testing samples. In general, we expect a normal distribution like this.
As we can see, the average error is around 1%.
Additionally, the errors histogram shows the distribution of the errors from the neural network on the testing samples. In general, we expect a normal distribution like this.
 As we can observe, most of the errors are around 0.
As we can observe, most of the errors are around 0.
6. Model deployment
Once we have tested the neural network’s generalization performance, we can save it for future use in the so-called model deployment mode. The mathematical expression represented by the neural network is the following:scaled_frequency_ghz = (frequency_ghz-2.408770084)/0.6040109992; scaled_length_patch_mm = (length_patch_mm-39.63669968)/20.70210075; scaled_width_patch_mm = (width_patch_mm-50.44079971)/34.84690094; scaled_area_patch_mm2 = (area_patch_mm2-2701.02002)/3742.169922; scaled_slot_length_mm = (slot_length_mm-19.39929962)/11.01990032; scaled_slot_width_mm = (slot_width_mm-26.85779953)/16.36989975; scaled_area_slot_mm2 = (area_slot_mm2-671.4219971)/1431.26001; perceptron_layer_1_output_0 = tanh( -6.33168 + (scaled_frequency_ghz*1.30197) + (scaled_length_patch_mm*1.41481) + (scaled_width_patch_mm*-2.04832) + (scaled_area_patch_mm2*0.646831) + (scaled_slot_length_mm*2.73) + (scaled_slot_width_mm*-1.89205) + (scaled_area_slot_mm2*0.0614876) ); perceptron_layer_1_output_1 = tanh( -2.28184 + (scaled_frequency_ghz*5.21126) + (scaled_length_patch_mm*0.803737) + (scaled_width_patch_mm*0.268686) + (scaled_area_patch_mm2*-0.136691) + (scaled_slot_length_mm*-0.161648) + (scaled_slot_width_mm*-2.42782) + (scaled_area_slot_mm2*2.42202) ); perceptron_layer_1_output_2 = tanh( 2.32082 + (scaled_frequency_ghz*-5.54642) + (scaled_length_patch_mm*-3.07181) + (scaled_width_patch_mm*1.70944) + (scaled_area_patch_mm2*0.455758) + (scaled_slot_length_mm*0.289671) + (scaled_slot_width_mm*2.28278) + (scaled_area_slot_mm2*-1.07915) ); perceptron_layer_2_output_0 = ( -5.7008 + (perceptron_layer_1_output_0*-5.91444) + (perceptron_layer_1_output_1*4.95589) + (perceptron_layer_1_output_2*5.0324) ); unscaling_layer_output_0=perceptron_layer_2_output_0*3.042239904-1.718469977;
References
- The data for this problem are available in kaggle repository.
