In this example, we build a machine learning model to predict whether a space flight succeeds or fails based on variables related to the mission.
Space missions have evolved greatly since the first launch in 1957.
Today, they are carried out by governments, private companies, and international organizations, aiming to explore the solar system and beyond.
These missions push the limits of science and technology while expanding human presence beyond Earth.
This example is solved with Neural Designer. To follow it step by step, you can use the free trial.
Contents
1. Application type
The variable to be predicted is binary. Therefore, this is a classification project.
The main goal is to model the state of the mission as a function of variables such as temperature, nature of the payload, payload target orbit, etc.
2. Dataset
The first step is to prepare the dataset, which is the source of information for the classification problem. It is composed of:
Data source
The file space_missions.csv contains the data for this example. Here, the number of variables (columns) is 33, and the number of samples (rows) is 166.
Variables
Below, we describe each variable:
Categorical variables
- company – Space company carrying out the flight (7 categories: SpaceX, Boeing, US Air Force, European Space Agency, Brazilian Space Agency, Arianespace, Martin Marietta).
- vehicle_type – Type of rocket vehicle (6 categories: Ariane, Delta, Falcon, Titan, VLS, Vega).
- payload_orbit – Target orbit for the payload (11 categories: Earth-Moon L2, Geostationary Transfer Orbit, Heliocentric Orbit, High Earth Orbit, Medium Earth Orbit, Low Earth Orbit, Mars Orbit, Polar Orbit, Suborbital, Sun-Synchronous Orbit, Sun/Earth Orbit).
Numerical variables
- temperature_f – Temperature at launch (°F).
- wind_speed_mph – Wind speed at launch (mph).
- humidity_pct – Humidity at launch (%).
- liftoff_thrust_kn – Rocket liftoff thrust (kN).
- payload_to_orbit_kg – Payload to orbit (kg).
- rocket_height_m – Rocket height (m).
- fairing_diameter_m – Rocket fairing diameter (m).
- payload_mass_kg – Payload mass (kg).
Target variables
mission_status – Target variable: success or failure.
Of the 33 variables, 32 are used as inputs, and the mission status variable is the target variable.
Samples
On the other hand, the dataset has 166 samples, and we split them randomly into 60% training, 20% selection, and 20% testing.
That gives us 90 samples for training, 30 for validation, and 30 for testing.
Once all the data set information has been set, we will perform some analytics to check the quality of the data.
For instance, we can calculate the data distribution. The following figure depicts the pie chart for the target variable.
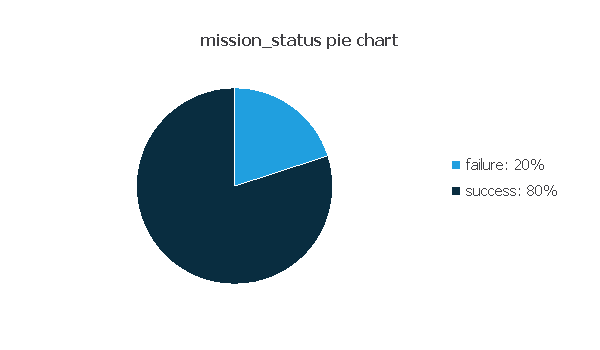
As we can see, the following chart illustrates the target ‘mission_status’ dependency with the 10 input columns with the greatest correlation in the data set.
The input-target correlations might help us see the different inputs’ influence on the mission status.
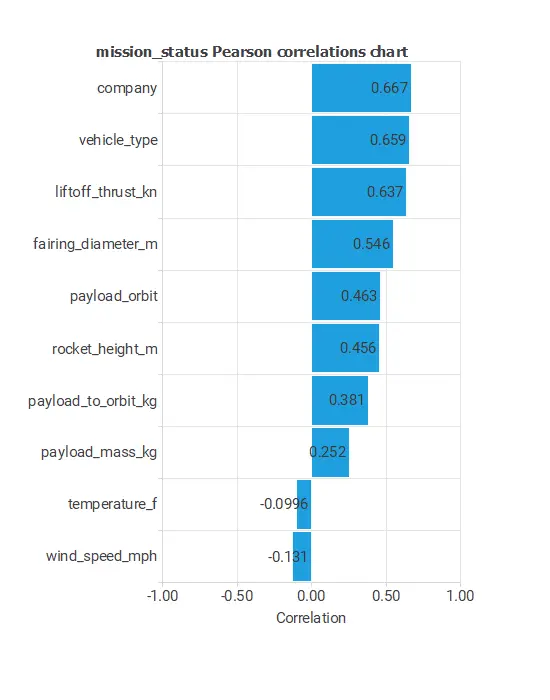
The chart above shows that the company has the most substantial impact on mission status, with a correlation of 0.667.
3. Neural network
The neural network will output the mission status as a function of the input variables described in the previous section.
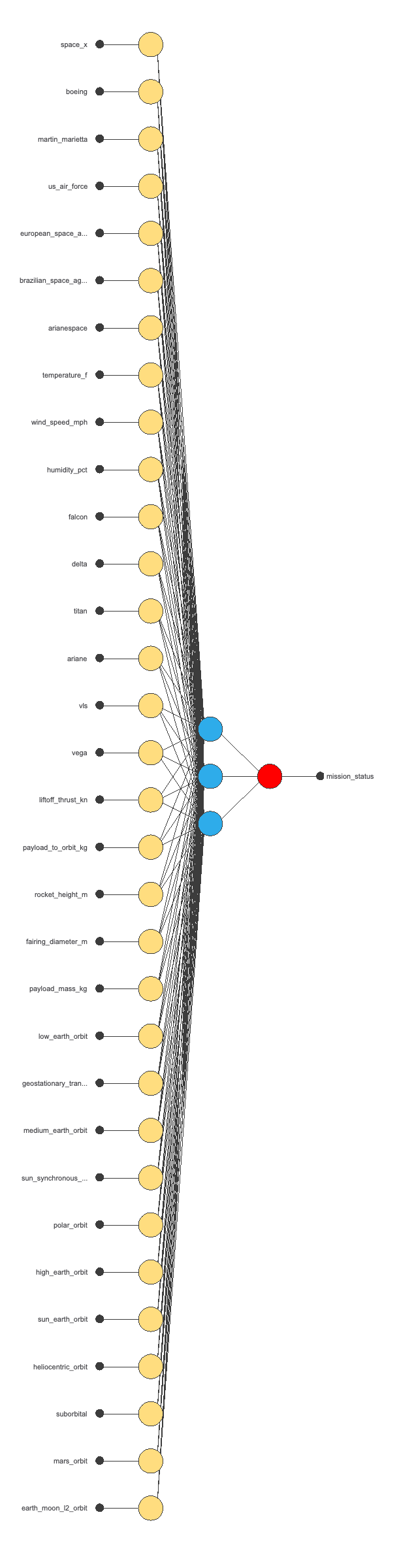
For this classification example, the neural network is composed of:
The scaling layer contains the statistics on the input calculated from the data file and the method for scaling the input variables. The minimum and maximum scaling methods are set here, but the mean and standard deviation scaling methods produce similar results.
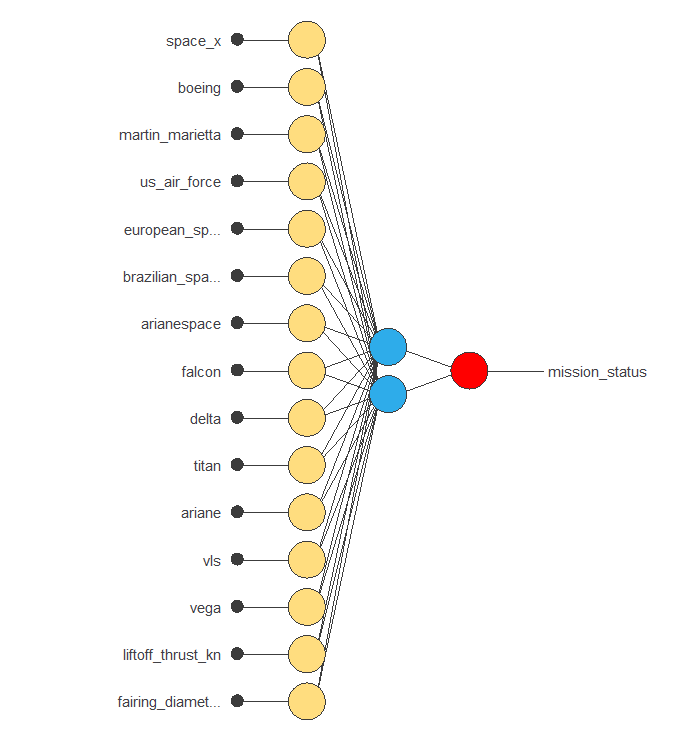
Initially, the number of inputs is 32, and there are 2 neurons in the perceptron layer, with the hyperbolic tangent as the activation function. The generalization study will eliminate variables that do not improve the predictive capabilities of the neural network from the scaling layer. It may also adjust the number of neurons in the perceptron layer until it finds the optimal complexity.
The next figure is the initial neural network architecture used in this example.
4. Training strategy
The training strategy is applied to the neural network to obtain the best possible performance. It is composed of two things:
Loss index
The error term fits the neural network to the training instances of the data set.
The regularization term makes the model more stable and improves generalization, so our model will be more predictive.
The selected loss index is the weighted squared error (WSE) with L2 regularization because, in this problem, the target samples aren’t balanced, as there are more cases where the mission status is 1 than where it’s 0.
Optimization algorithm
The selected optimization algorithm that minimizes the loss index is the quasi-Newton method.
The following table shows the operators, parameters, and stopping criteria of the quasi-Newton method used in this study.

5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties.
That is, we want to improve the final selection error by changing the number of inputs or the number of neurons in the perceptron layer.
The best selection error is achieved using a model whose complexity is the most appropriate to produce a better data fit.
Order selection algorithms are responsible for finding the optimal number of perceptron neurons in the neural networks.
After performing neuron selection and input selection, the model is set at an optimal 2 neurons in the perceptron layer and 4 inputs in the scaling layer (company, vehicle type, lift-off thrust, and fairing diameter).
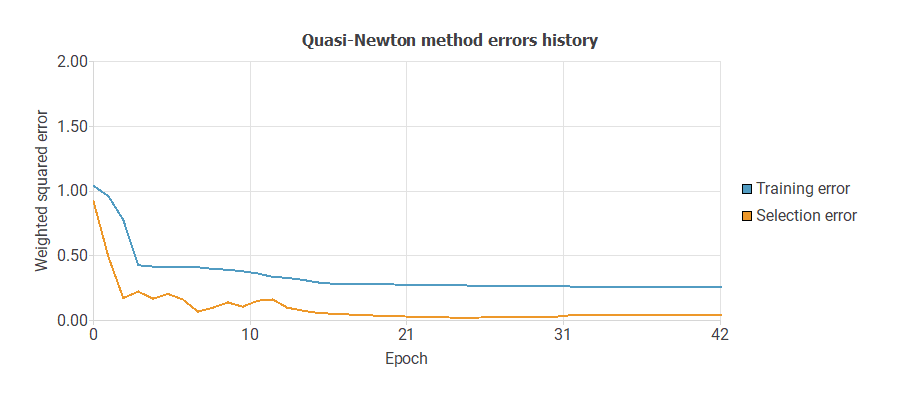
The following chart shows how the training error (blue) and selection error (orange) decrease with the training epochs.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network. The testing compares the values provided by this technique to the observed values.
Roc curve
A good measure of the precision of a binary classification model is the ROC curve.
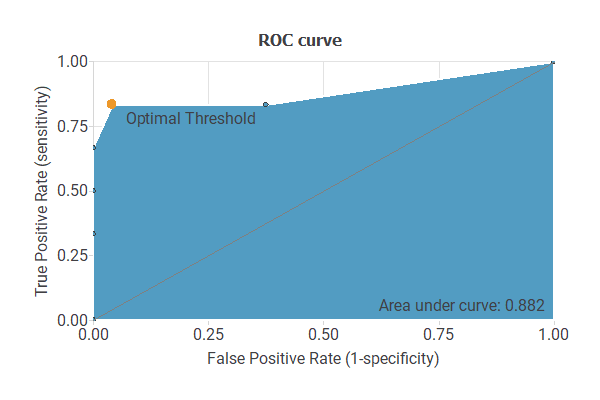
We are interested in the area under the curve (AUC). A perfect classifier would have an AUC=1, and a random one would have an AUC=0.5. Our model has an AUC of 0.882, which is a good indicator of our model’s performance.
Confusion matrix
We can also look at the confusion matrix. Next, we show the elements of this matrix:
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 24 (80.0%) | 0 (0.0%) |
| Real negative | 2 (6.7%) | 4 (13.3%) |
Binary classification metrics
From the above confusion matrix, we can calculate the following binary classification tests:
- Classification accuracy: 93.3% (ratio of correctly classified samples).
- Error rate: 6.7% (ratio of misclassified samples).
- Sensitivity:100% (percentage of actual positives classified as positive).
- Specificity: 66.7% (percentage of actual negatives classified as negative).
7. Model deployment
After testing, the model is ready to estimate the mission status of new space missions with satisfactory quality over the same data range.
To classify any given star, we calculate the neural network outputs from the different variables: temperature, luminosity, relative radius, absolute magnitude, color, and spectral class.
For example, if we introduce the following values for each input:
- Company: Boeing
- Vehicle Type: delta
- Liftoff Thrust (kN): 5668.36
- Fairing Diameter (m): 4.25
- Mission status: 0.9=success
The model predicts a mission_status value of 0.9, which means that the mission is a success for those variables.
References
- Space missions data set from the Kaggle repository.
