The volume, variety, and velocity of information stored in security and crime prevention institutions have increased significantly.
The intelligent analysis of all that data can substantially help those security forces adopt these techniques.
This study applies predictive analytics in law, crime, and law enforcement. In particular, we build a neural network to recognize patterns of criminal behavior based on location and time variables. This predictive model will allow security forces to optimize their resources and prevent crimes before they happen.
The developed algorithm can predict crime categories at a given date, time, and district. Moreover, we can plot the predictions as heat maps, which allows the development of new innovative city systems that could help in the fight against crime.
Contents:
1. Introduction
According to classical theories of criminality, recent literature focuses on the impact of socioeconomic and demographic variables on different types of crime.
So far, the development of efficiency indicators has helped governments in their efforts to increase efficiency.
In addition, it has facilitated police work regarding crime prevention, criminal investigation, apprehension, order maintenance, and citizen service.
This work incorporates new methodologies based on machine learning and neural networks to the aforementioned traditional concepts. These new methods will improve the allocation of resources to police departments worldwide in their fight against crime.
2. Application type
The variable to be predicted is continuous (criminal activity). Therefore, this is an approximation project.
This work aims to demonstrate the ability of neural networks to predict the criminal activity that will occur in the City of San Francisco based on spatial and temporal variables.
We will see how a predictive model could help the security forces of a given city to be more efficient in their allocation of resources. We also include crime predictions for a given day at different times.
3. Data set
The original data set contains incidents derived from the SFPD (San Francisco Police Department) Crime Incident Reporting System.
The data ranges from 01/01/2003 to 05/13/2015. In particular, it includes 878,049 incident reports with the following variables: day, category, description, weekday, police district, resolution, address, coordinate X, and coordinate Y.
The first step is to prepare the data set, which is the source of information for the approximation problem. The original data set is unsuitable for building a criminality model, so it was subjected to a detailed pre-processing.
We have taken into account two types of variables:
- As inputs, we selected the day, month, day of the week, and time.
- As outputs, we have the number of crimes for every section and police district in periods of six hours (00:00-6:00, 6:00-12:00, 12:00-18:00, and 18:00-24:00).
The City of San Francisco has ten police districts. The following figure shows this division.

Based on the offenses listed in the San Francisco data set and the ICCS (International Classification of Crime for Statistical Purposes) classification, we conclude that the following types of reports could be grouped in the following sections:
- Section 1: No data available.
- Section 2: Driving under alcohol influence, extortion, and kidnapping.
- Section 3: Pornography/obscenity, non-forcible sex offenses, and forcible sex offenses.
- Section 4: Assault, robbery, and stolen property.
- Section 5: Vandalism, burglary, larceny/theft, and vehicle theft.
- Section 6: Drugs/narcotics and liquor laws.
- Section 7: Bad checks, bribery, embezzlement, forgery/counterfeiting, and fraud.
- Section 8: Disorderly conduct, drunkenness, prostitution, gambling, loitering, and runaway.
- Section 9: Weapons law.
- Section 10: Arson.
- Section 11: Fairly offenses, other offenses, and secondary codes.
Neural networks work with numerical values. However, some of the variables in the data set have categorical values.
Therefore, the first step is to assign numerical values to all categorical variables.
- DAY: The day is a numerical value ranging from 1 to 31 for the days in a month.
- MONTH: For the twelve months of the year (from January to December), we have assigned numbers from 1 to 12.
- YEAR: The data we have goes from 2003 to 2015.
Therefore, the year is a numerical value that ranges from 2003 to 2015. - WEEKDAY: For the seven days a week (from Monday to Sunday), we have assigned numbers from 1 to 7.
- TIME: We divided the 24 hours in a day into four-time frames and assigned each time frame a number, as shown in the table below,
| TIME FRAME | NUMBER ASSIGNED |
|---|---|
| 00:00-6:00 | 1 |
| 6:00-12:00 | 2 |
| 12:00-18:00 | 3 |
| 18:00-24:00 | 4 |
- NUMBER OF CRIMES PER POLICE DISTRICT: We want to predict this variable. As shown in the figure of the distribution of police departments in the city of San Francisco, there are ten police districts in San Francisco:
Bayview, Central, Ingleside, Mission, Northern, Park, Richmond, Southern, Taraval, and Tenderloin.
The data set contains information about the number of crimes committed at a given time in one of these districts.This variable is numerical, so it doesn’t require any changes.
The variables are of two types:
- Input variables: these are the predictors of the criminality model (day, month, year, weekday, and time).
- Target variables: this is the variable to be predicted: crime count per police department at a given time frame for every section.
On the other hand, cases can be of three types:
- Training cases are used to build different criminality models with different topologies.
- Selection cases are used to select the criminality model with the best predictive capabilities.
- Test cases are used to validate the performance of the criminality model.
The following pie chart details the uses of all cases in the data set.
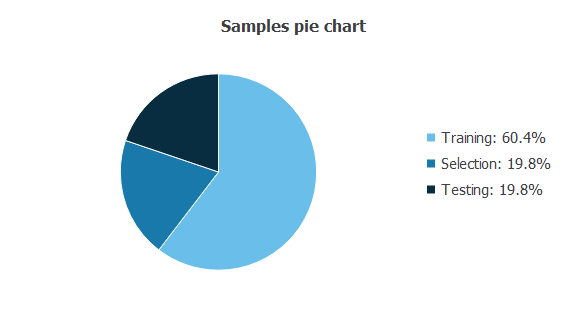
The data is divided into training, selection, and testing subsets, comprising 60%, 20%, and 20% of the instances.
This results in 11,302 cases for training, 3,676 for selection, and 3,676 for testing for each section.
Statistics
Basic statistics are valuable information when designing a model since they give important insights into our application.
The total number of crimes in the data set is 674,656. They comprise the period from 01/01/2003 to 05/13/2015.
Therefore, the average number of crimes per day is 149.59. The following table shows that the district with the lowest offenses is Richmond, and the community with the highest number is Southern.
| Count | Crimes/day | |
|---|---|---|
| Bayview | 72560 | 16.088 |
| Central | 69252 | 15.355 |
| Ingleside | 65140 | 14.443 |
| Mission | 96218 | 21.334 |
| Northern | 87380 | 19.374 |
| Park | 37930 | 8.410 |
| Richmond | 36860 | 8.172 |
| Southern | 118323 | 26.235 |
| Taraval | 52963 | 11.743 |
| Tenderloin | 64829 | 14.374 |
The most common crime types are those belonging to Section 5 (vandalism, burglary, larceny/theft, and vehicle theft), totaling 310,160 offenses.
On the other hand, Section 10 (arson) has the lowest rate, with 1,513 crimes reported in total. The following table shows those statistics:
| Count | Crimes/day | |
|---|---|---|
| Section 2 | 4865 | 1.078 |
| Section 3 | 4558 | 1.010 |
| Section 4 | 104415 | 23.151 |
| Section 5 | 310160 | 68.771 |
| Section 6 | 55874 | 12.388 |
| Section 7 | 29149 | 6.463 |
| Section 8 | 19401 | 4.301 |
| Section 9 | 8555 | 1.896 |
| Section 10 | 1513 | 0.335 |
| Section 11 | 136167 | 30.192 |
Finally, if we calculate the statistics by type of crime and location, the combination of Southern and Section 5 has the highest number of crimes (57,961).
On the other hand, the combination of Tenderloin and Section 10 has the lowest number (60). The following table shows all of the above.
| Section 2 | Section 3 | Section 4 | Section 5 | Section 6 | Section 7 | Section 8 | Section 9 | Section 10 | Section 11 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Bayview | 505 | 411 | 12969 | 26623 | 4612 | 1830 | 876 | 1647 | 393 | 18715 |
| Central | 408 | 403 | 9486 | 38258 | 1946 | 3745 | 1933 | 487 | 111 | 9605 |
| Ingleside | 583 | 526 | 11668 | 27901 | 2479 | 2353 | 577 | 1130 | 182 | 14503 |
| Mission | 695 | 756 | 15408 | 34410 | 9252 | 3487 | 6017 | 1329 | 145 | 20769 |
| Northern | 515 | 449 | 11658 | 46179 | 4635 | 3550 | 2942 | 789 | 149 | 13232 |
| Park | 278 | 218 | 4647 | 18610 | 2722 | 1564 | 1159 | 357 | 65 | 6628 |
| Richmond | 446 | 227 | 4195 | 19886 | 1080 | 1838 | 387 | 327 | 103 | 6157 |
| Southern | 684 | 840 | 17068 | 57961 | 9613 | 6172 | 2159 | 1128 | 185 | 22513 |
| Taraval | 429 | 402 | 7099 | 26319 | 1653 | 2793 | 953 | 567 | 120 | 9597 |
| Tenderloin | 322 | 326 | 10217 | 14013 | 17882 | 1817 | 2398 | 794 | 60 | 14447 |
The data set used to design the approximation model that predicts city crime contains the number of crimes for all sections and districts over 4 hours.
For each section, we have a data set of 18,385 instances and 15 variables (day, month, year, weekday, time, and the number of crimes for the police districts Bayview, Central, Ingleside, Mission, Northern, Park, Richmond, Southern, Taraval, and Tenderloin). The total number of data is 275,775.
The table below shows the minimums, maximums, means, and standard deviations of the data corresponding to Section 5 crimes (burglary, larceny/theft, vandalism, and vehicle theft).
As we can see, the district with the most crimes is the Southern.
| Minimum | Maximum | Mean | Deviation | |
|---|---|---|---|---|
| Day | 1 | 31 | ||
| Month | 1 | 12 | ||
| Year | 2003 | 2015 | ||
| Weekday | 1 | 7 | ||
| Time | 1 | 4 | ||
| Bayview | 0 | 19 | 2.960 | 1.644 |
| Central | 0 | 22 | 4.254 | 2.121 |
| Ingleside | 0 | 20 | 3.102 | 1.725 |
| Mission | 0 | 22 | 3.826 | 1.992 |
| Northern | 0 | 30 | 5.135 | 2.555 |
| Park | 0 | 17 | 2.069 | 1.326 |
| Richmond | 0 | 16 | 2.211 | 1.413 |
| Southern | 0 | 38 | 6.445 | 3.095 |
| Taraval | 0 | 20 | 2.926 | 1.662 |
| Tenderloin | 0 | 15 | 1.558 | 1.089 |
Histograms show the distribution of the data over their entire range. For example, the following figure is a histogram of Section 5 crimes in Southern.

This histogram has a normal distribution centered on 5.7 crimes per 4 hours.
4. Neural network
A neural network is a biologically inspired computational model with a network architecture composed of artificial neurons. These are information-processing structures whose most significant property is their ability to learn how to perform specific tasks, such as discovering relationships, recognizing patterns, forecasting trends, or finding associations.
In general, the learning problem of a neural network resides in deriving a function from a data set. The targets specify what output responses the neural network should produce from the inputs. In our specific problem, we want to model a crime prediction function based on input data regarding time and location.
The crime model represents a neural network with a single hidden layer of hyperbolic tangent neurons and a linear output layer.
No more hidden layers are needed, for this is a class of universal approximators.
For each section, the neural network has five inputs (day, month, year, weekday, and time) and ten output neurons (the number of crimes in that period for each district).
5. Training strategy
While the problem constrains the number of inputs and output neurons, hidden neurons are a design variable. Therefore, we performed a detailed order selection analysis to draw the optimal network architecture.
The loss index chosen for this application is the normalized squared error between the outputs from the neural network and the targets in the data set.
This error is a very standard loss index in data modeling. A regularization term is added to the loss expression to obtain smooth solutions.
The selected training algorithm for solving the problem is a quasi-Newton method with BFGS training direction and Brent optimal training rate. This training algorithm is a standard method that performs well for small and big problems.
The following figure shows the network architecture resulting from this analysis. The yellow circles represent scaling neurons, the blue circles represent perceptron neurons, and the red circles represent unscaling neurons. As we can see, the optimal order here is 6, the number of neurons in the first layer of perceptrons.

6. Testing analysis
We calculated the errors between the neural network outputs and their corresponding targets in the testing set to test the model’s predictive capabilities. Table 5 shows the results given by this testing analysis for each district.
Here, the mean errors lie in the range of 5-10%, which are good numbers for this kind of problem.
| District | Mean error (%) |
|---|---|
| Bayview | 8.902 |
| Central | 7.818 |
| Ingleside | 7.966 |
| Mission | 8.371 |
| Northern | 6.862 |
| Park | 9.382 |
| Richmond | 8.946 |
| Shouthern | 6.041 |
| Taraval | 7.394 |
| Tenderloin | 7.875 |
From the table above, we can see that the neural network predicts crime rates with reasonable accuracy. The neural network is now ready to move to the production phase.
7. Model deployment
The following figure shows the crime predictions of Section 5 for a Thanksgiving Day (23rd of November, Thursday), in the period 00:00-06:00. As we can see, most districts have low rates, but Southern, which has a medium rate.

Similarly, the following figure shows the exact predictions for 06:00-12:00. As displayed, an increase is observed. Again, southern, Northern, and Central districts present the highest ratios, while Tenderloin shows the lowest. Bayview, Mission, Ingleside, Park, Richmond, and Taraval are in the middle.

As the day progresses, in the time zone 12:00-18:00, the Southern District will reach a high worrying ratio. The Central and Northern districts will also be at risk. The Tenderloin, Richmond, and Park districts will no longer be as secure as earlier, and the Bayview, Ingleside, Mission, and Taraval districts will be at intermediate risk.

The highest ratios will occur late evening (18:00-24:00), especially in Southern, Central, and Northern districts. The ratios will be intermediate in Bayview, Ingleside, Mission, and Taraval districts (also in Tenderloin). On the other hand, the districts of Richmond and Park will prescribe the lowest ratios.

We can also look at how crimes will evolve with time. For example, the following figure shows the evolution of Section 5 offenses in Southern during a whole week and 12:00-18:00.

As we can see, the number of crimes increases throughout the week, from Sunday to Saturday.
Conclusions
In this study, we have used machine learning based on neural networks to aid the police forces of the City of San Francisco. Like many others globally, this city is increasing the volume, variety, and velocity of information stored about crimes.
By recognizing criminal behavior patterns based on temporal and spatial variables, we have designed a predictive model to optimize police resources to prevent crimes before they happen.
- We have observed how Section 5 crimes in the Southern District represent the darkest points of criminality in the City of San Francisco.
- Section 10 crimes in the Tenderloin District have the smallest number of crimes in that city.
- The predictive model shows how Section 5 crimes increase as the day progresses, making the 18:00-24:00 period the most dangerous, especially in the Southern, Central, and Northern Districts.
- Conversely, the lowest ratios for that section occur in the 00:00-06:00 period in the Tenderloin district.
Because of the crime maps and evolution graphs generated as examples, we could observe clusters of crime areas and periods.
This allows the police to allocate their resources at the place and when crimes are to be produced, avoiding crime and reducing risk to citizens.
The study reflected in this chapter leads us to conclude the great capacity neural networks provide when working on crime prevention. Implementing these systems in the SFPD will better allocate human resources. That will result in greater efficiency of those police forces.
At the same time, these advanced analytics methods improve the existing ones that turn around traditional socioeconomic and demographic variables and usually use Data Envelopment Analysis as an optimization technique for inputs/outputs.
References:
- The data set used in this study contains incidents reported by the San Francisco Police Department (SFPD) and it is being published by San Francisco Open Data, the central clearinghouse for data published by the City and County of San Francisco.
- The International Classification of Crime for Statistical Purposes (ICCS).
Related posts:
No related posts.