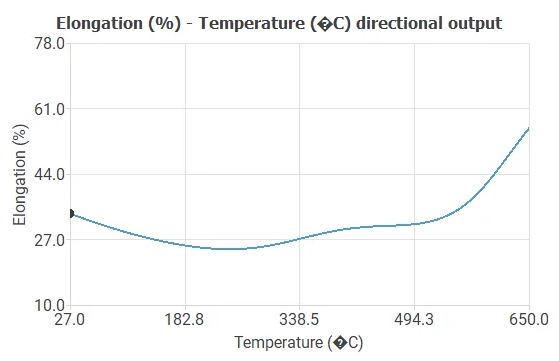
This example applies machine learning to predict steel properties using only element concentrations and temperature.
Thank you for reading this post, don't forget to subscribe!Machine learning is well-suited for this problem because it can learn complex, non-linear relationships between composition, temperature, and steel properties directly from data.
Unlike traditional theoretical methods, it does not require simplifying assumptions, and unlike physical testing, it provides faster and more cost-effective predictions across a wide range of compositions.
This example is solved with Neural Designer.
To follow it step by step, you can use the free trial.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
1. Application type
The variables to be predicted are continuous. Therefore, this is an approximation project.
The primary goal is to model those properties as a function of the percentages of different materials alloyed and the temperature.
2. Data set
The first step is to prepare the data set, which is the primary source of information. It is composed of:
- Data source.
- Variables.
- Instances.
Data source
The data file LowAlloySteels.csv contains 20 columns and 915 samples. All variables are continuous.
Variables
The variables of the problem are:
Identifier
- Alloy_code – Identifier for each alloy.
Input variables
- C – Carbon concentration (%).
- Si – Silicon concentration (%).
- Mn – Manganese concentration (%).
- P – Phosphorus concentration (%).
- S – Sulfur concentration (%).
- Ni – Nickel concentration (%).
- Cr – Chromium concentration (%).
- Mo – Molybdenum concentration (%).
- Cu – Copper concentration (%).
- V – Vanadium concentration (%).
- Al – Aluminum concentration (%).
- N – Nitrogen concentration (%).
- Ceq – Carbon equivalent (%).
- Nb+Ta – Niobium + Tantalum concentration (constant, set as unused).
- Temperature_C – Temperature in °C.
Target variables
- 0.2_Proof_Stress – Stress at 0.2% plastic strain (MPa).
- Tensile_Strength – Maximum stress before breaking (MPa).
- Elongation – Deformation before fracture under tensile load (%).
- Reduction_in_Area – Reduction in cross-sectional area before fracture (%).
Our target variables will be the last four 0.2% Proof Stress, Tensile Strength, Elongation, and Reduction in Area.
In this case, we focus on Elongation, so we select as Unused the other variables.
The process for the other properties is the same.
Instances
This data set contains 915 instances.
From these, 549 instances are used for training (60%), 183 for generalization (20%), and 183 for testing (20%).
Variable distributions
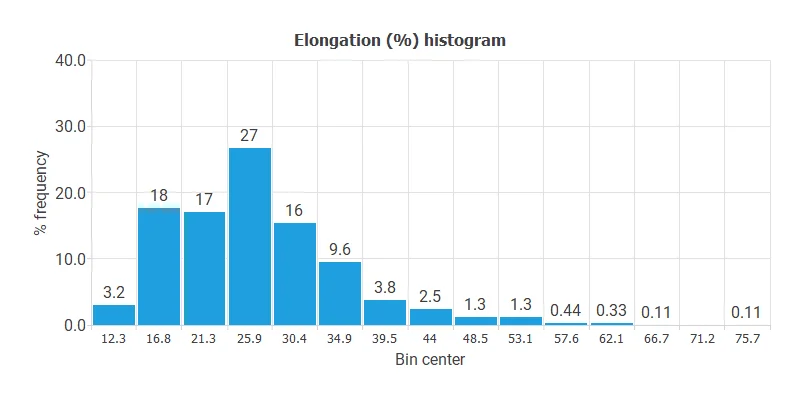
Calculating the data distributions helps us detect anomalies and errors.
The following chart shows the histogram for the Elongation.
Inputs-targets correlations
It is also helpful to check dependencies between input and target variables. For this, we can plot an input–target correlation chart.
In this case, the figure below shows the elongation correlation chart.
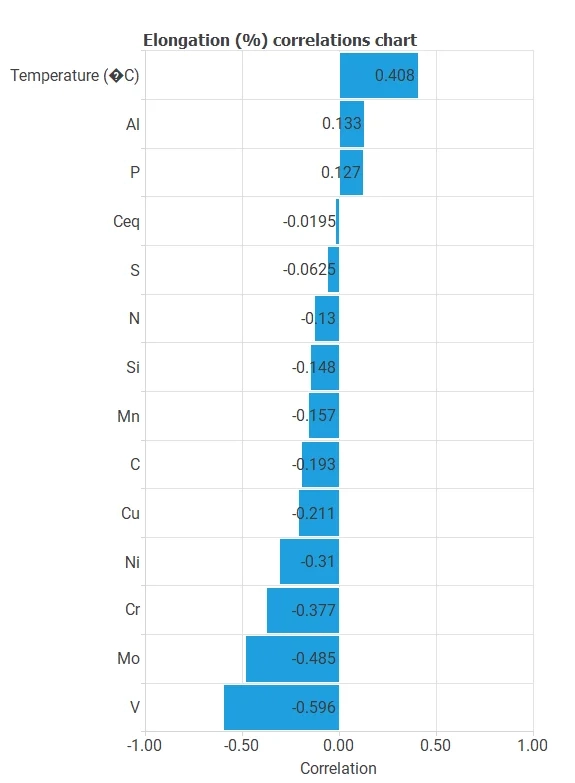
The above chart shows that the Vanadium percentage is the variable most strongly correlated with the elongation.
3. Neural network
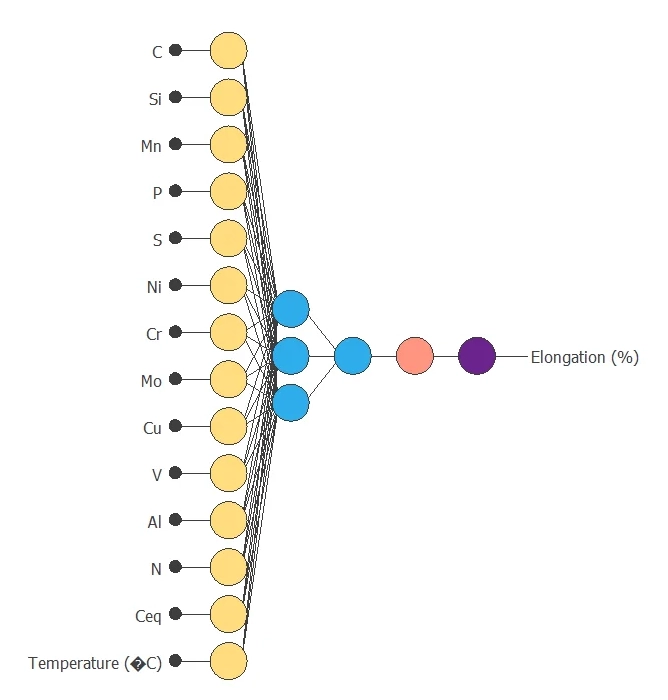
The next step is to build a neural network representing the approximation function.
The neural network has 14 inputs (Temperature and percentages of distinct metals alloyed) and 1 output.
For approximation problems, it is usually composed of:
Scaling layer
The scaling layer contains the statistics on the inputs.
We use the automatic setting for this layer to accommodate the best scaling technique for our data.
Dense layers
We use 2 perceptron layers here:
- The first perceptron layer has 14 inputs, 3 neurons, and a hyperbolic tangent activation function
- The second perceptron layer has 3 inputs, 1 neuron, and a linear activation function
Unscaling layer
The unscaling layer contains the statistics of the output. We use the automatic method as before.
Neural network graph
The following figure shows the neural network structure that has been set for this data set.
4. Training strategy
The fourth step is to select an appropriate training strategy, defining what the neural network will learn.
- A loss index.
- An optimization algorithm.
Loss index
The loss index. defines the quality of the learning. It is composed of an error term and a regularization term.
The error term chosen is the normalized squared error. It divides the squared error between the neural network outputs and the data set’s targets by its normalization coefficient.
If it takes a value of 1 then the neural network predicts the data “in the mean”, while a value of zero means a perfect data prediction.
The regularization term is L2 regularization. It is applied to control the neural network’s complexity by reducing the values of its parameters.
Optimization algorithm
The optimization algorithm is in charge of searching for the neural network that minimizes the loss index.
Here, we choose the Levenberg-Marquardt as the optimization algorithm.
Training
The following chart shows how training and selection errors decrease with the epochs during training.
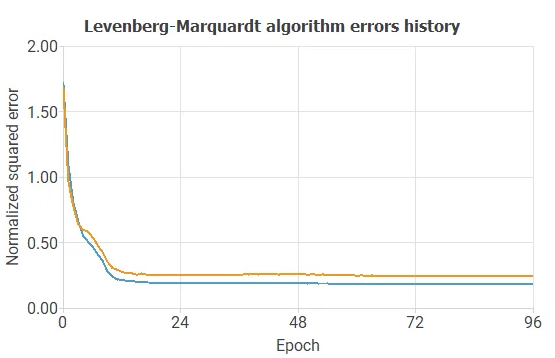
The final values are training error = 0.182 NSE and selection error = 0.245 NSE, respectively.
5. Model selection
To improve the selection error, 0.245 NSE, and the predictions made by the model, we can perform Model Selection algorithms on the structure.
The best selection error is achieved by using a model whose complexity is optimal to produce an adequate data fit.
We use order selection algorithms that find the optimal number of perceptrons in the neural network.
For example, we have the incremental order algorithm.
The blue line shows the training error versus the number of neurons, while the orange line shows the selection error versus the number of neurons.
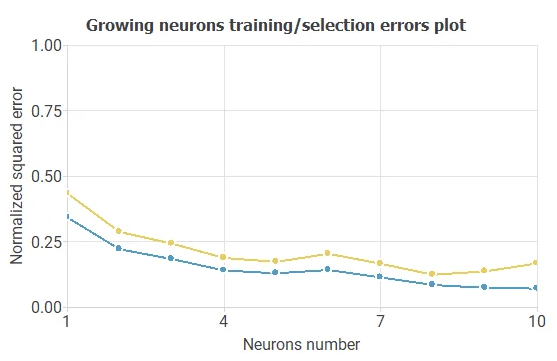
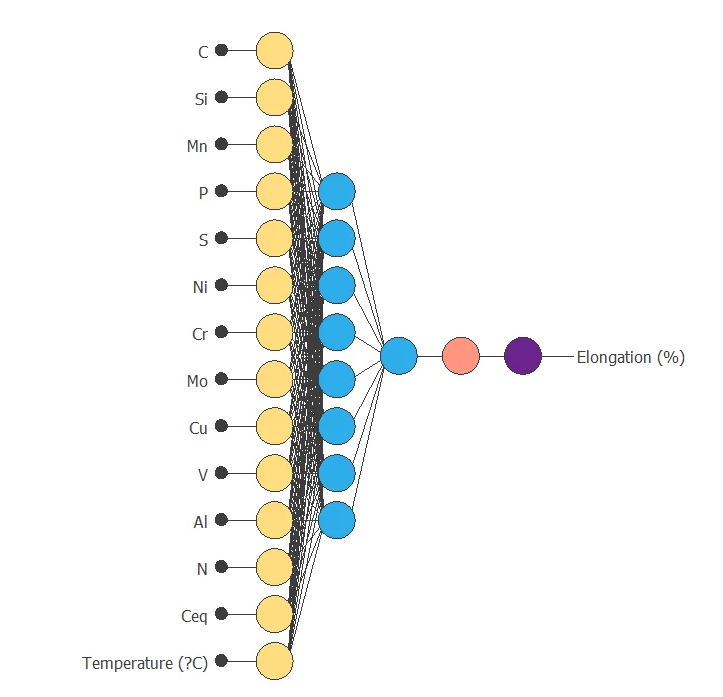
As a result, we obtained a final selection error of 0.123 NSE with 8 neurons.
The following figure shows the optimal network architecture for this case.
6. Testing analysis
Now, we perform various tests to validate our model and assess the quality of the predictions.
Goodness-of-fit
In this case, we perform a linear regression analysis between the predicted and the real values. The following figure shows this relation.
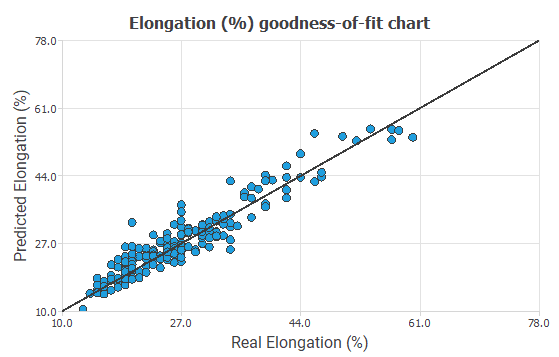
The correlation value is R2=0.886, which is close to 1.
7. Model deployment
Now we can use the model to estimate the elongation of some variables, or calculate a new estimation with the model.
Response optimization
For example, you can minimize the Elongation, maintaining the proportion of carbon greater than 0.2.
The following table summarizes the conditions for this problem.
| Variable name | Condition |
|---|---|
| C | Greater than 0.2 |
| Si | None |
| Mn | None |
| P | None |
| S | None |
| Ni | None |
| Cr | None |
| Mo | None |
| Cu | None |
| V | None |
| Al | None |
| N | None |
| Ceq | None |
| Temperature | None |
| Elongation | Minimize |
And the results of our model are :
- C: 0.25%
- Si: 0.412%
- Mn: 0.65%
- P: 0.012%
- S: 0.009%
- Ni: 0.096%
- Cr: 0.44%
- Mo: 0.3958%
- Cu: 0.19%
- V: 0.106%
- Al: 0.37%
- N: 0.004%
- Ceq: 0.1377%
- Temperature: 149.725 ºC
- Elongation: 10.4633%
Directional outputs
Directional outputs let you observe how results change when varying one input while keeping the others fixed.
References
- Kaggle open repository: Mechanical properties of low alloy steels.
