1. Application type.
2. Data set.
3. Neural network.
4. Training strategy.
5. Model selection.
6. Testing analysis.
7. Model deployment.

1. Application type

This is a classification project since the variable to be predicted is binary: Higgs boson or not.

The LHC produces over ten million collisions per hour. Approximately 300 of them result in a Higgs boson. These events are saved to disk, providing about one billion events and three petabytes of raw data per year to be analyzed to obtain evidence of the Higgs boson.

Among these events, we distinguish between the ones that produce a Higgs boson (signal) and the uninteresting ones (background), which previous experiments have discovered. The problem is identifying each event when there is such a large amount of data.

Scientists have worked together to provide solutions to this problem. On the one hand, we use numerical methods to classify these events, such as a boosted decision tree. On the other hand, we can perform numerical simulations capable of reproducing the signal event where the Higgs boson appears. These simulations provide numerical values for the variables observed with the ATLAS detector.

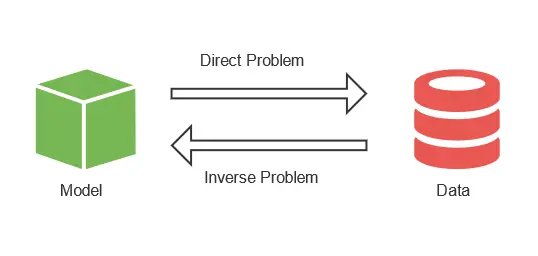
The issue is that we have to classify the raw data obtained in the detector using the data from the simulation. This is an inverse problem, where we start from the solution and obtain the problem’s variables afterward.

In the simulation, we can replicate as many collisions that produce Higgs bosons as we want. This way, we can have similar percentages of both Higgs bosons and uninteresting events. Once we have this data, we create a model to classify the events. It is necessary to use machine learning techniques to obtain a good classification model to detect the Higgs boson. The neural network we obtain gives us the probability that a particle is a Higgs boson from the variables observed by the detector. Finally, we apply this model to the actual data from the LHC. As a result, scientists only have to analyze the particles with a high probability of being a Higgs boson.

2. Data set

The first step is to prepare the data set, which is the source of information for the classification problem. It is composed of:

• Data source.
• Variables.
• Instances.

Data source

The data source is the file Higgs.csv. It contains the data for this example in CSV (comma-separated values) format. The number of columns is 28, and the number of rows is 10012.

The data set consists of 11 million simulated events using the official ATLAS full detector simulator. For this example, we have reduced the instances to around 10000. The proton-proton collisions are simulated based on all scientists’ knowledge of particle physics. Next, the resulting particles from the collisions are tracked through a virtual model of the detector.

Each event is described by 28 different features, such as the estimated mass of the Higgs boson candidate or the missing transverse energy.

Variables

The next table shows the variables of the data set for a better understanding of it:

Instances

The instances are divided into training, selection, and testing subsets. They represent 60% (6008), 20% (2002), and 20% (2002), respectively, and are split at random.

Variables distributions

We can calculate the distributions of all variables. The following is the pie chart for the Higgs boson vs. background cases.

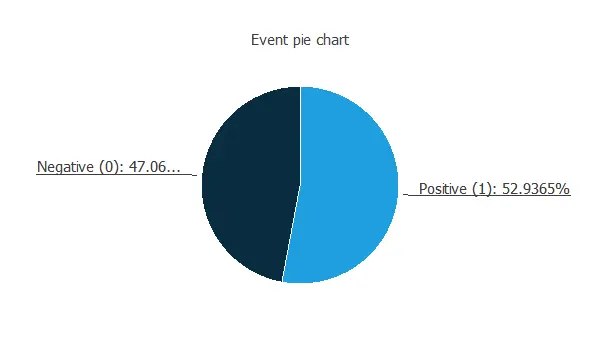
We can see a very similar number of samples for both categories. This is because we have manipulated the data set for better predictions.
In reality, the background cases represent the majority of the events.

3. Neural network

The second step is to choose a neural network. Classification models usually contain the following layers:

• A scaling layer.
• Two perceptron layers.
• A probabilistic layer.

The scaling layer contains the statistics of the inputs calculated from the data file and the method for scaling the input variables. Here, the minimum-maximum method has been set. Nevertheless, the mean-standard deviation method would produce very similar results.

The number of perceptron layers is one, and it has 4 neurons.

Finally, we set the binary probabilistic method for the probabilistic layer, as we want the predicted target variable to be binary.

The next figure is a graph depicting this classification neural network:

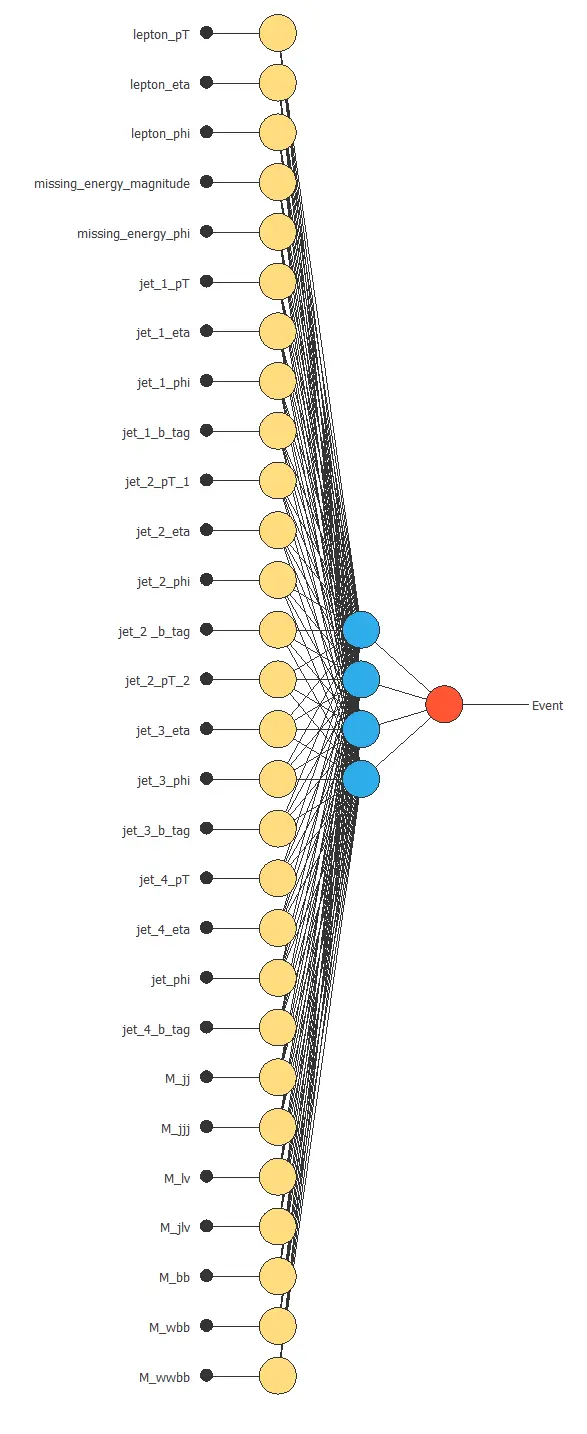
Here, the yellow circles represent scaling neurons, the blue circles are the perceptron neurons, and the red circles are the probabilistic neurons. The number of inputs is 28, and the number of outputs is 1.

4. Training strategy

The fourth step is to set the training strategy, which is composed of:

• Loss index.
• Optimization algorithm.

The loss index we choose for this application is the weighted squared error with L2 regularization.

The error term fits the neural network to the training instances of the data set. The regularization term makes the model more stable and improves generalization.

The optimization algorithm searches for the neural network parameters that minimize the loss index. Here, we choose the quasi-Newton method.

The following chart shows how training and selection errors decrease with the epochs during training.

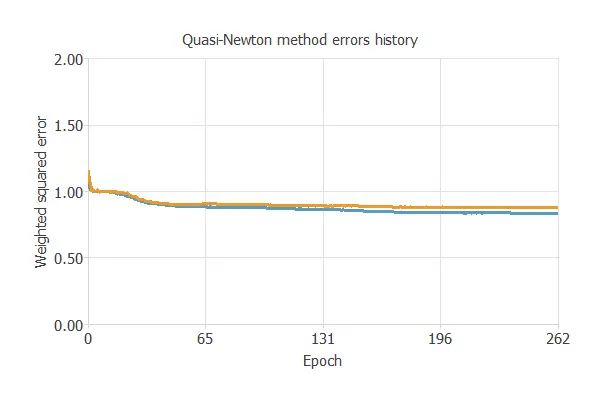
The final values are training error = 0.837 NSE (blue) and selection error = 0.880 NSE (orange).

5. Model selection

The objective of model selection is to find the network architecture with the best generalization properties, which minimizes the error on the selected instances of the data set.

More specifically, we want to find a neural network with a selection error of less than 0.880 WSE, which is the value we have achieved so far.

Order selection algorithms train several network architectures with different numbers of neurons and select the one with the smallest selection error.

The incremental order method starts with a few neurons and increases the complexity at each iteration.

6. Testing analysis

The last step is to test the generalization performance of the trained neural network.

The testing analysis aims to validate the model’s generalization ability after training it. Specifically, for a classification technique, we need to compare the values predicted by the model to the observed values. We can use the ROC curve, the standard testing method for binary classification projects.

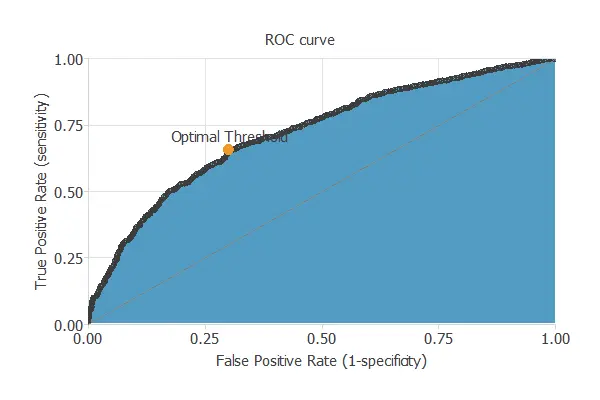
In this case, the area under the ROC curve is 0.720.

In the confusion matrix, the rows represent the targets (or real values), and the columns correspond to the outputs (or predictive values).
The diagonal cells show the correctly classified cases, and the off-diagonal cells show the misclassified cases.

The number of instances the model can correctly predict is 1340 (66.9%), while it misclassifies 662 (33.1%).

The binary classification tests shown in the next picture provide us with some useful information about the performance of the model:

Test
Description
Value

Classification accuracy
Ratio of instances correctly classified.
67%

Error rate
Ratio of instances misclassified.
33%

Sensitivity
Portion of real positives which the model predicts as positives.
71%

Specificity
Portion of real negatives that the model predicts as negatives.
62%

The classification accuracy, the proportion of instances the model can correctly classify, is 0.669 (66.9%). The error rate, which is the ratio of misclassified instances, is 0.331 (33.1%).

7. Model deployment

Once we have tested the model, Neural Designer allows us to obtain its mathematical expression. With it, we can analyze more than four million events per second.

The following listing represents the mathematical expression of the trained neural network.

scaled_lepton_pT = lepton_pT*(1+1)/(6.699999809-(0.275000006))-0.275000006*(1+1)/(6.699999809-0.275000006)-1;
scaled_lepton_eta = lepton_eta*(1+1)/(2.430000067-(-2.430000067))+2.430000067*(1+1)/(2.430000067+2.430000067)-1;
scaled_lepton_phi = lepton_phi*(1+1)/(1.74000001-(-1.74000001))+1.74000001*(1+1)/(1.74000001+1.74000001)-1;
scaled_missing_energy_magnitude = missing_energy_magnitude*(1+1)/(5.820000172-(0.01240000036))-0.01240000036*(1+1)/(5.820000172-0.01240000036)-1;
scaled_missing_energy_phi = missing_energy_phi*(1+1)/(1.74000001-(-1.74000001))+1.74000001*(1+1)/(1.74000001+1.74000001)-1;
scaled_jet_1_pT = jet_1_pT*(1+1)/(7.059999943-(0.1589999944))-0.1589999944*(1+1)/(7.059999943-0.1589999944)-1;
scaled_jet_1_eta = jet_1_eta*(1+1)/(2.970000029-(-2.940000057))+2.940000057*(1+1)/(2.970000029+2.940000057)-1;
scaled_jet_1_phi = jet_1_phi*(1+1)/(1.74000001-(-1.74000001))+1.74000001*(1+1)/(1.74000001+1.74000001)-1;
scaled_jet_1_b_tag = jet_1_b_tag*(1+1)/(2.170000076-(0))-0*(1+1)/(2.170000076-0)-1;
scaled_jet_2_pT_1 = jet_2_pT_1*(1+1)/(5.190000057-(0.1899999976))-0.1899999976*(1+1)/(5.190000057-0.1899999976)-1;
scaled_jet_2_eta = jet_2_eta*(1+1)/(2.910000086-(-2.910000086))+2.910000086*(1+1)/(2.910000086+2.910000086)-1;
scaled_jet_2_phi = jet_2_phi*(1+1)/(1.74000001-(-1.74000001))+1.74000001*(1+1)/(1.74000001+1.74000001)-1;
scaled_jet_2 _b_tag = jet_2 _b_tag*(1+1)/(2.210000038-(0))-0*(1+1)/(2.210000038-0)-1;
scaled_jet_2_pT_2 = jet_2_pT_2*(1+1)/(6.519999981-(0.2639999986))-0.2639999986*(1+1)/(6.519999981-0.2639999986)-1;
scaled_jet_3_eta = jet_3_eta*(1+1)/(2.730000019-(-2.730000019))+2.730000019*(1+1)/(2.730000019+2.730000019)-1;
scaled_jet_3_phi = jet_3_phi*(1+1)/(1.74000001-(-1.74000001))+1.74000001*(1+1)/(1.74000001+1.74000001)-1;
scaled_jet_3_b_tag = jet_3_b_tag*(1+1)/(2.549999952-(0))-0*(1+1)/(2.549999952-0)-1;
scaled_jet_4_pT = jet_4_pT*(1+1)/(6.070000172-(0.3650000095))-0.3650000095*(1+1)/(6.070000172-0.3650000095)-1;
scaled_jet_4_eta = jet_4_eta*(1+1)/(2.5-(-2.5))+2.5*(1+1)/(2.5+2.5)-1;
scaled_jet_phi = jet_phi*(1+1)/(1.74000001-(-1.74000001))+1.74000001*(1+1)/(1.74000001+1.74000001)-1;
scaled_jet_4_b_tag = jet_4_b_tag*(1+1)/(3.099999905-(0))-0*(1+1)/(3.099999905-0)-1;
scaled_M_jj = M_jj*(1+1)/(13.10000038-(0.1720000058))-0.1720000058*(1+1)/(13.10000038-0.1720000058)-1;
scaled_M_jjj = M_jjj*(1+1)/(7.389999866-(0.3420000076))-0.3420000076*(1+1)/(7.389999866-0.3420000076)-1;
scaled_M_lv = M_lv*(1+1)/(3.680000067-(0.4609999955))-0.4609999955*(1+1)/(3.680000067-0.4609999955)-1;
scaled_M_jlv = M_jlv*(1+1)/(6.579999924-(0.3840000033))-0.3840000033*(1+1)/(6.579999924-0.3840000033)-1;
scaled_M_bb = M_bb*(1+1)/(8.260000229-(0.08100000024))-0.08100000024*(1+1)/(8.260000229-0.08100000024)-1;
scaled_M_wbb = M_wbb*(1+1)/(4.75-(0.3889999986))-0.3889999986*(1+1)/(4.75-0.3889999986)-1;
scaled_M_wwbb = M_wwbb*(1+1)/(4.320000172-(0.4449999928))-0.4449999928*(1+1)/(4.320000172-0.4449999928)-1;
perceptron_layer_0_output_0 = tanh[ -1.37262 + (scaled_lepton_pT*-0.258746)+ (scaled_lepton_eta*0.0362805)+ (scaled_lepton_phi*-0.0832154)+ (scaled_missing_energy_magnitude*0.0609962)+ (scaled_missing_energy_phi*0.0118553)+ (scaled_jet_1_pT*-0.273796)+ (scaled_jet_1_eta*0.0535145)+ (scaled_jet_1_phi*0.0226441)+ (scaled_jet_1_b_tag*-0.0632788)+ (scaled_jet_2_pT_1*-0.112196)+ (scaled_jet_2_eta*0.0415722)+ (scaled_jet_2_phi*0.112501)+ (scaled_jet_2 _b_tag*-0.0129353)+ (scaled_jet_2_pT_2*-0.358131)+ (scaled_jet_3_eta*0.0191431)+ (scaled_jet_3_phi*-0.064177)+ (scaled_jet_3_b_tag*0.0189284)+ (scaled_jet_4_pT*0.157812)+ (scaled_jet_4_eta*-0.113475)+ (scaled_jet_phi*0.113226)+ (scaled_jet_4_b_tag*-0.0288421)+ (scaled_M_jj*0.928491)+ (scaled_M_jjj*1.56142)+ (scaled_M_lv*0.168347)+ (scaled_M_jlv*0.280415)+ (scaled_M_bb*-2.39201)+ (scaled_M_wbb*-1.74089)+ (scaled_M_wwbb*-1.1966) ];
perceptron_layer_0_output_1 = tanh[ 0.0302904 + (scaled_lepton_pT*0.931957)+ (scaled_lepton_eta*-0.107117)+ (scaled_lepton_phi*0.123916)+ (scaled_missing_energy_magnitude*0.829294)+ (scaled_missing_energy_phi*0.16022)+ (scaled_jet_1_pT*0.136368)+ (scaled_jet_1_eta*0.660784)+ (scaled_jet_1_phi*0.185285)+ (scaled_jet_1_b_tag*0.397167)+ (scaled_jet_2_pT_1*-0.412377)+ (scaled_jet_2_eta*-0.263695)+ (scaled_jet_2_phi*-0.0766151)+ (scaled_jet_2 _b_tag*-0.0693654)+ (scaled_jet_2_pT_2*-0.603738)+ (scaled_jet_3_eta*-0.363455)+ (scaled_jet_3_phi*-0.223806)+ (scaled_jet_3_b_tag*0.0319366)+ (scaled_jet_4_pT*-0.696683)+ (scaled_jet_4_eta*-0.35523)+ (scaled_jet_phi*-0.0530527)+ (scaled_jet_4_b_tag*-0.0545712)+ (scaled_M_jj*0.0526469)+ (scaled_M_jjj*-0.267477)+ (scaled_M_lv*-0.355338)+ (scaled_M_jlv*-0.269982)+ (scaled_M_bb*0.0216565)+ (scaled_M_wbb*-0.837428)+ (scaled_M_wwbb*1.08876) ];
perceptron_layer_0_output_2 = tanh[ -0.63821 + (scaled_lepton_pT*0.812243)+ (scaled_lepton_eta*0.0253617)+ (scaled_lepton_phi*-0.104747)+ (scaled_missing_energy_magnitude*0.182205)+ (scaled_missing_energy_phi*-0.325033)+ (scaled_jet_1_pT*-0.82733)+ (scaled_jet_1_eta*-0.802168)+ (scaled_jet_1_phi*-0.314119)+ (scaled_jet_1_b_tag*-0.107867)+ (scaled_jet_2_pT_1*-0.982512)+ (scaled_jet_2_eta*0.217818)+ (scaled_jet_2_phi*0.161883)+ (scaled_jet_2 _b_tag*0.0279769)+ (scaled_jet_2_pT_2*-0.283825)+ (scaled_jet_3_eta*0.186862)+ (scaled_jet_3_phi*0.0681052)+ (scaled_jet_3_b_tag*-0.090589)+ (scaled_jet_4_pT*0.167979)+ (scaled_jet_4_eta*0.00966222)+ (scaled_jet_phi*-7.93182e-05)+ (scaled_jet_4_b_tag*-0.0425335)+ (scaled_M_jj*0.232803)+ (scaled_M_jjj*0.123681)+ (scaled_M_lv*-0.129535)+ (scaled_M_jlv*0.4562)+ (scaled_M_bb*-0.144573)+ (scaled_M_wbb*-1.02725)+ (scaled_M_wwbb*0.318511) ];
perceptron_layer_0_output_3 = tanh[ 0.448874 + (scaled_lepton_pT*1.25716)+ (scaled_lepton_eta*-0.112071)+ (scaled_lepton_phi*0.0693822)+ (scaled_missing_energy_magnitude*0.200465)+ (scaled_missing_energy_phi*-0.179459)+ (scaled_jet_1_pT*0.983861)+ (scaled_jet_1_eta*-0.259419)+ (scaled_jet_1_phi*-0.139325)+ (scaled_jet_1_b_tag*0.224549)+ (scaled_jet_2_pT_1*-0.820891)+ (scaled_jet_2_eta*0.0750885)+ (scaled_jet_2_phi*0.0114138)+ (scaled_jet_2 _b_tag*-0.0692787)+ (scaled_jet_2_pT_2*-0.105241)+ (scaled_jet_3_eta*-0.12762)+ (scaled_jet_3_phi*-0.0696983)+ (scaled_jet_3_b_tag*-0.139342)+ (scaled_jet_4_pT*-0.3681)+ (scaled_jet_4_eta*-0.140406)+ (scaled_jet_phi*-0.135149)+ (scaled_jet_4_b_tag*-0.109267)+ (scaled_M_jj*-0.867477)+ (scaled_M_jjj*-0.309968)+ (scaled_M_lv*-0.0646885)+ (scaled_M_jlv*0.667318)+ (scaled_M_bb*-0.464598)+ (scaled_M_wbb*1.94239)+ (scaled_M_wwbb*-0.978041) ];
probabilistic_layer_combinations_0 = -0.685385 +2.9533*perceptron_layer_0_output_0 -2.104*perceptron_layer_0_output_1 -2.1637*perceptron_layer_0_output_2 +2.63699*perceptron_layer_0_output_3 
Event = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);

As mentioned, we solved this example with the data science and machine learning platform Neural Designer.

References

• We have obtained the data for this problem from the UCI Machine Learning Repository.
•  P. Baldi, P. Sadowski, and D. Whiteson. Searching for Exotic Particles in High-energy Physics with Deep Learning. Nature Communications 5 (July 2, 2014).

Related posts