Contents
- 1. Perceptron layer.
- 2. Probabilistic layer.
- 3. Long-short term memory (LSTM) layer.
- 4. Scaling layer.
- 5. Unscaling layer.
- 6. Bounding layer.
- 7. Network architecture.
- 8. Model parameters.
- 9. Approximation neural networks.
- 10. Classification neural networks.
- 11. Forecasting neural networks.
1. Perceptron layer
The most critical layers of a neural network are the perceptron layers (also called dense layers). Indeed, they allow the neural network to learn.
The following figure shows a perceptron layer. It receives information as a set of numerical inputs. The neural network combines this information with the biases and weights. Finally, the combinations are activated to produce the final outputs.
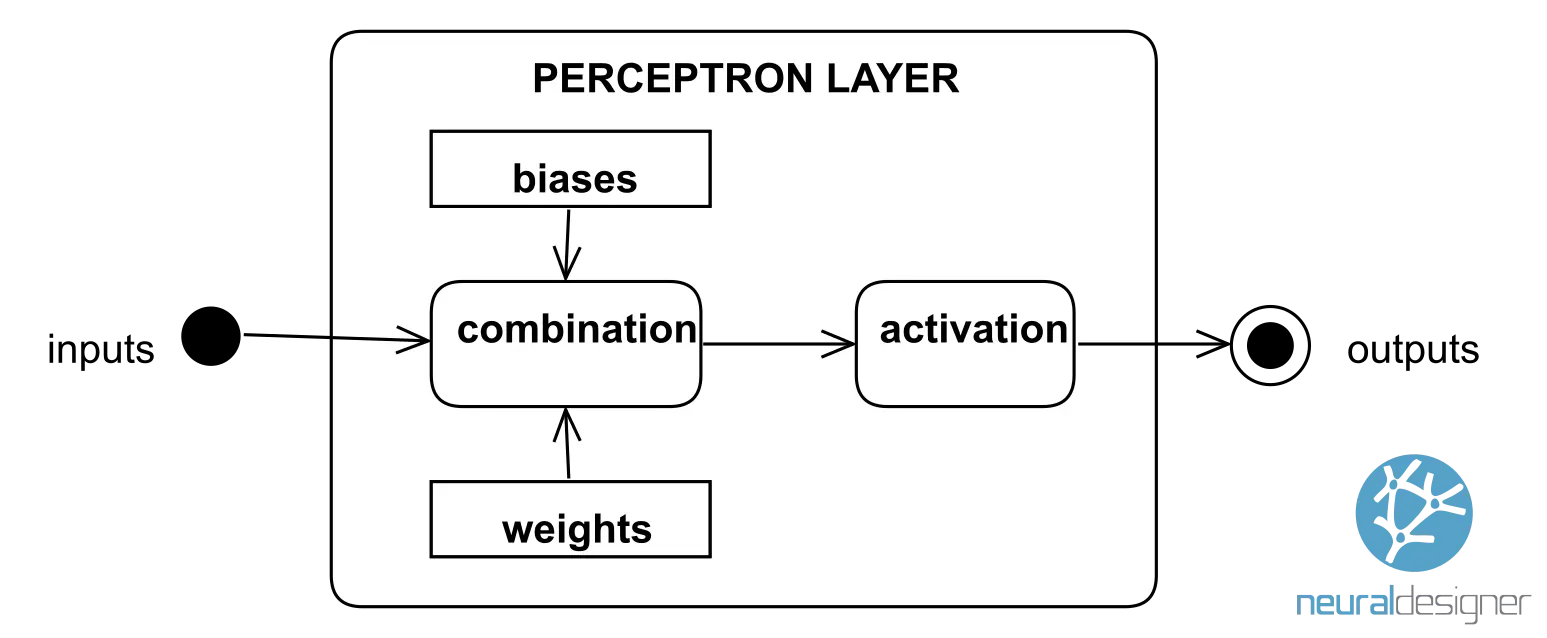
The activation function determines the function that the layer represents. Some of the most common activation functions are the following:
- Linear activation function.
- Hyperbolic tangent activation function.
- Logistic activation function.
- Rectified linear (ReLU) activation function.
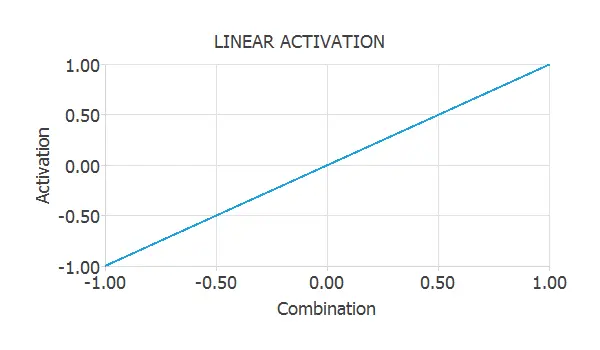
Linear activation function
The output of a perceptron with a linear activation function is simply the combination of that neuron.
$$ activation = combination $$
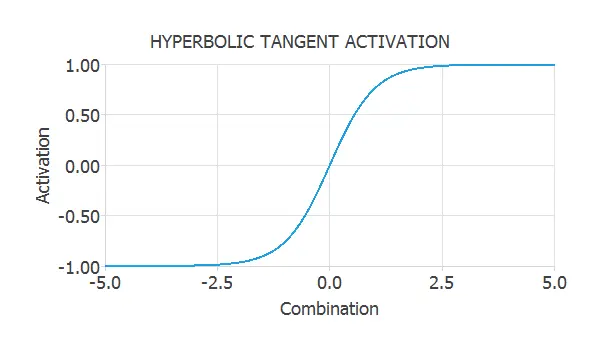
Hyperbolic tangent activation function
The hyperbolic tangent is one of the most used activation functions when constructing neural networks. It is a sigmoid function which varies between -1 and +1.
$$ activation = tanh(combination) $$
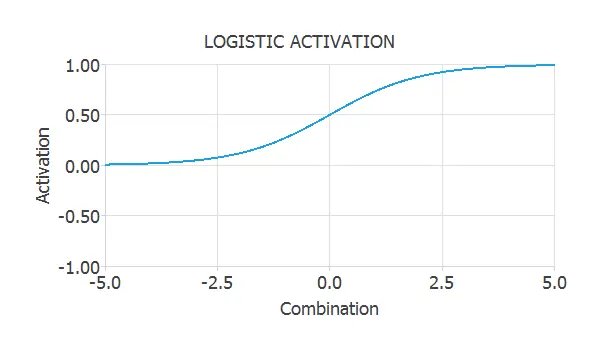
Logistic activation function
The logistic is another type of sigmoid function. It is very similar to the hyperbolic tangent, but in this case, it varies between 0 and 1. $$ activation = frac{1}{1+e^{-combination}} $$
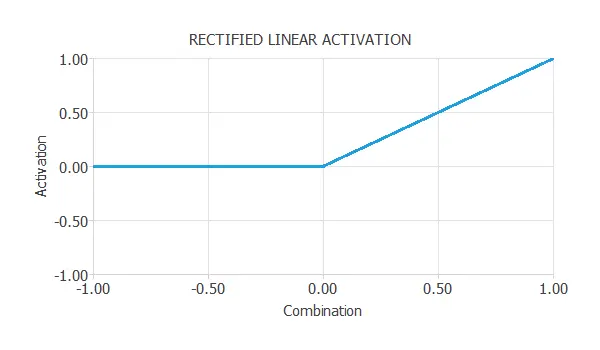
Rectified linear (ReLU) activation function
The rectified linear activation function, or ReLU, is one of the most used activation functions. It is zero when the combination is negative and equal to when the combination is zero or positive.
$$activation = left{ begin{array}{lll}
0 &if& textrm{$combination < 0$} \
combination &if& textrm{$combination geq 0$}
end{array} right. $$
You can read the article Perceptron: The main component of neural networks for a more detailed description of this critical neuron model.
In this regard, a perceptron layer is a group of neurons connecting to the same inputs and sending outputs to the same destinations.
2. Probabilistic layer
In classification problems, outputs are usually interpreted as class membership probabilities. In this way, the probabilistic outputs will fall in the range [0, 1], and the sum will be 1. The probabilistic layer provides outputs that can be interpreted as probabilities.
The following figure shows a probabilistic layer. It is very similar to the perceptron layer, but the activation functions are restricted to be probabilistic.
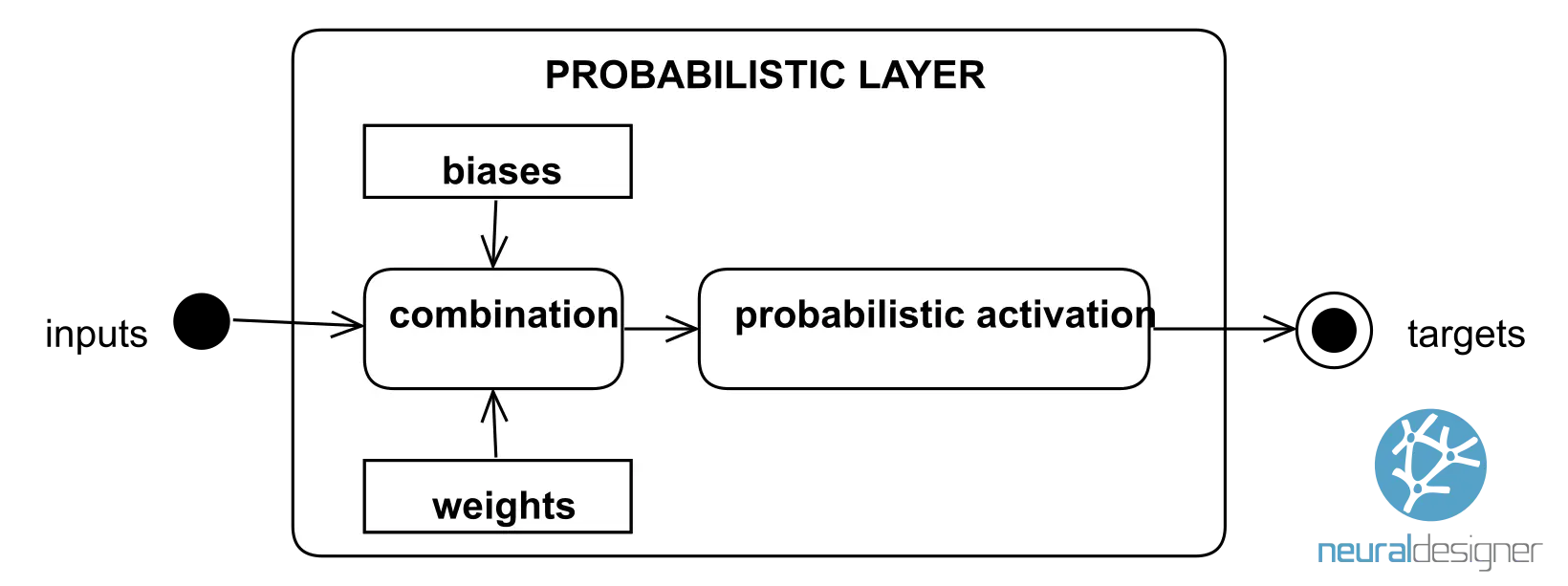
Some of the most popular probabilistic activations are the following:
Logistic probabilistic activation
The logistic activation function is used in binary classification applications. As we know, it is a sigmoid function that varies between 0 and 1.
$$ probabilistic_activation = frac{1}{1+e^{-combination}} $$
SoftMax probabilistic activation
This method is used in multiple classification problems. It is a continuous probabilistic function, which holds that the outputs always fall in the range [0, 1], and the sum of all is always 1.
$$probabilistic_activation = frac{e^{combination}}{sum e^{combinations}}$$
3. Long-short-term memory (LSTM) layer
Long-short-term memory (LSTM) layers are a particular recurrent layer widely used in forecasting applications.
The following figure shows an LSTM layer. It receives information as a set of numerical inputs. This information is processed through forget, input, state, and output gates and stored in hidden and cell states. Finally, the layer produces the final outputs.
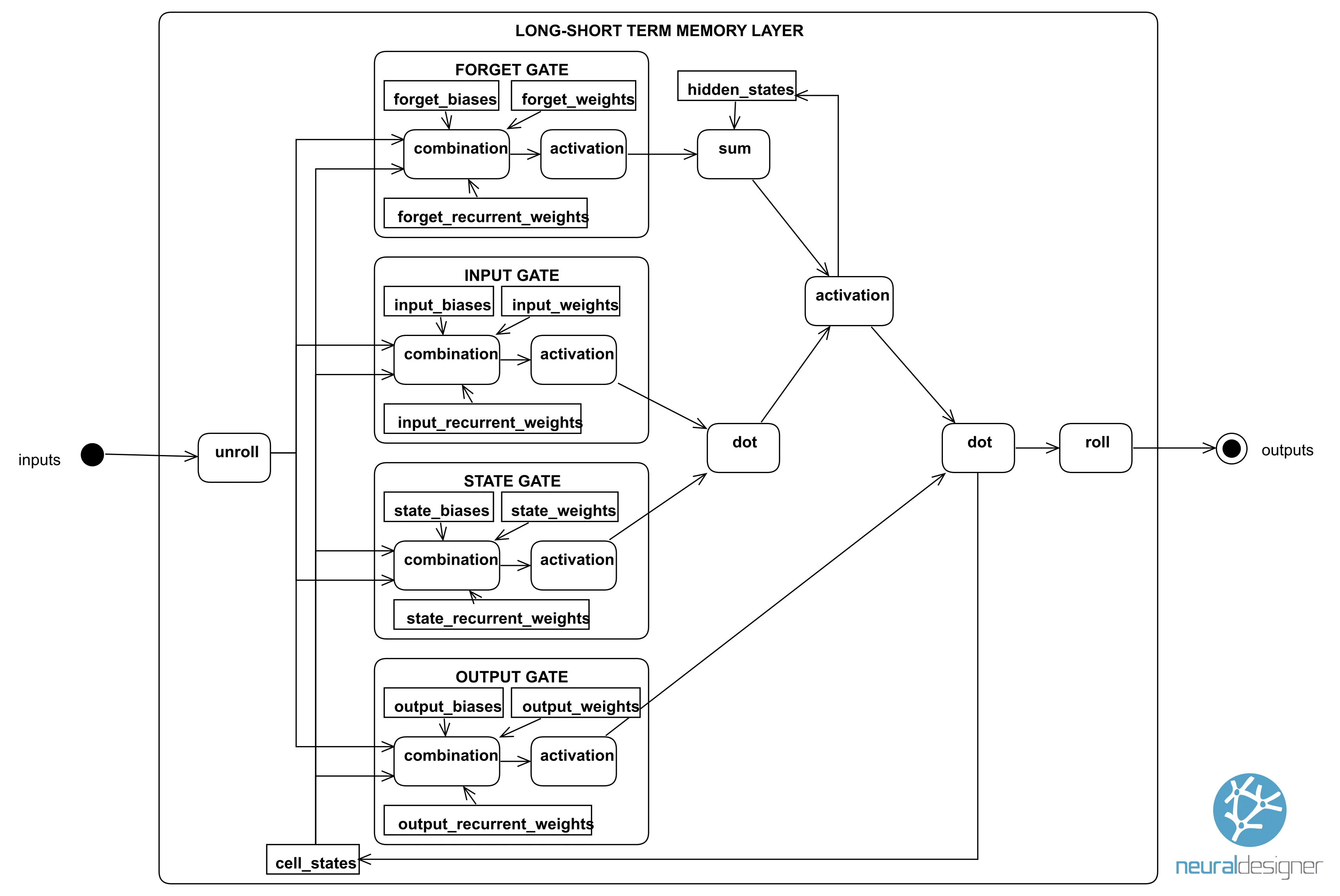
As we can see, long-short-term memory (LSTM) layers are complex and contain many parameters. That structure makes them suitable for learning dependencies from time-series data.
4. Scaling layer
In practice, scaling the inputs to give them a proper range is always convenient. In the context of neural networks, the scaling layer performs this process.
The scaling layer contains some basic statistics on the inputs. They include the mean, standard deviation, minimum, and maximum values.
Some scaling methods used in practice are the following:
- Minimum and maximum scaling method.
- Mean and standard deviation scaling method.
- Standard deviation scaling method.
Minimum and maximum scaling method
The minimum and maximum methods produce a data set scaled between −1 and 1. This method is usually applied to variables with a uniform distribution.
$$ scaled_input = -1+frac{(input-minimum)cdot (1-(-1))}{maximum-minimum}$$
Mean and standard deviation scaling method
The mean and standard deviation method scales the inputs to have a mean of 0 and a standard deviation of 1. This method usually applies to normal (or Gaussian) distribution variables.
$$ scaled_input = frac{input-mean}{standard_deviation}$$
Standard deviation scaling method
The standard deviation scaling method produces inputs with standard deviation 1. This is typically applied to half-normal distributions, variables centered at zero with only positive values.
$$ scaled_input = frac{input}{standard_deviation}$$
All scaling methods are linear and, in general, produce similar results. In all cases, synchronizing the scaling of the inputs in the dataset with the scaling of the inputs in the neural network is necessary. Neural Designer does that without any intervention by the user.
5. Unscaling layer
The scaled outputs from a neural network are unscaled to produce the original units. In the context of neural networks, the unscaling layer does this.
An unscaling layer contains some basic statistics on the outputs. They include the mean, standard deviation, minimum, and maximum values.
Four unscaling methods are utilized in practice:
- Minimum and maximum unscaling method.
- Mean and standard deviation unscaling method.
- Standard deviation unscaling method.
- Logarithmic unscaling method.
Minimum and maximum unscaling method
The minimum and maximum method unscales variables that have been previously scaled to have minimum -1 and maximum +1, to produce outputs in the original range,
$$ unscaled_output = minimum\+scaled_outputcdot(maximum-minimum)$$
Mean and standard deviation unscaling method
The mean and standard deviation method unscales variables that have been previously scaled to have mean 0 and standard deviation 1,
$$ unscaled_output = mean\+scaled_outputcdot standard_deviation $$
Standard deviation unscaling method
The standard deviation method unscales variables that have been previously scaled to have a standard deviation of 1, to produce outputs in the original range,
$$ unscaled_output = scaled_outputcdot standard_deviation$$
Logarithmic unscaling method
The logarithmic method unscales variables that have undergone a logarithmic transformation previously.
$$ unscaled_output = minimum\+0.5(exp{(scaled_output)}+1)(maximum-minimum)$$
In all cases, synchronizing the scaling of the targets in the dataset with unscaling the outputs in the neural network is necessary. Neural Designer does that without any intervention by the user.
6. Bounding layer
The output needs to be limited between the two values in many cases. For instance, the quality of a product might range from 1 to 5 stars.
The bounding layer performs this task. It uses the following formula:
$$bounded_output = left{ begin{array}{l}
lower_bound, quad textrm{$output < lower_bound$} \
output, quad textrm{$lower_bound leq output leq upper_bound$} \
upper_bound, quad textrm{$output geq upper_bound$}
end{array} right. $$
7. Network architecture
A neural network can be symbolized as a graph, where nodes represent neurons, and edges represent connectivities among neurons. An edge label represents the parameter of the neuron for which the flow goes in.
Most neural networks, even biological neural networks, exhibit a layered structure. Therefore, layers are the basis for determining the architecture of a neural network.
We build a neural network by organizing layers of neurons in a network architecture. The characteristic network architecture in this case is known as the feed-forward architecture. In a feed-forward neural network, we group layers into a sequence so that neurons in any layer connect only to neurons in the next layer.
The following figure represents a neural network with four inputs, several layers of different types, and three outputs.
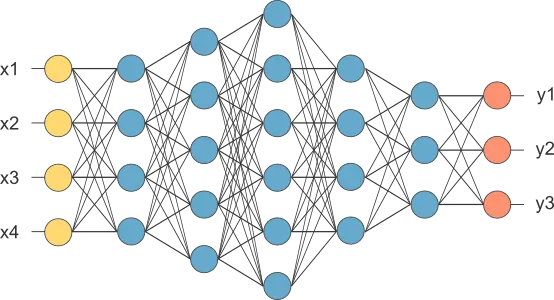
8. Model parameters
The model parameters involve the parameters of each layer in the network architecture.
You can group all these parameters into a vector (theta), which you can write as:
$$theta = left(theta_1,ldots,theta_d right).$$
The number of adaptable parameters, (d), is the sum of parameters in each layer.
As we have seen, a neural network may consist of various types of layers, depending on the requirements of the predictive model.
Next, we describe each application type’s most common neural network configurations.
9. Approximation neural networks
An approximation model usually contains a scaling layer, several perceptron layers, an unscaling layer, and a bounding layer.
Two layers of perceptrons will be enough to represent the data set most of the time. Very complex models might require deeper architectures with three, four, or more layers of perceptrons.
The following figure represents a neural network to estimate the power generated by a combined cycle power plant as a function of meteorological and plant variables.
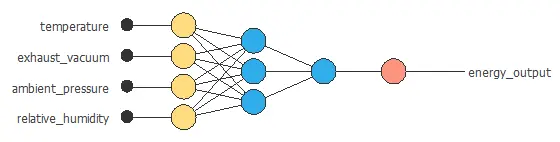
The above neural network has four inputs and one output. It consists of a scaling layer (yellow), a perceptron layer with four neurons (blue), a perceptron layer with one neuron (blue), and an unscaling layer (red).
10. Classification neural networks
A classification model usually requires a scaling layer, one or several perceptron layers, and a probabilistic layer. It might also contain a principal component layer.
Two layers of perceptrons will be enough to represent the data set most of the time.
The following figure is a binary classification model for diagnosing breast cancer from fine-needle aspirates.
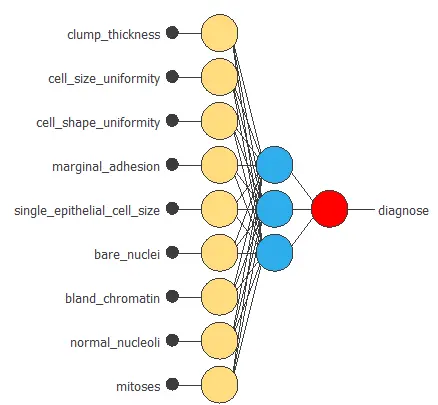
The above neural network has nine inputs and one output. It consists of a scaling layer (yellow), a perceptron layer with three neurons (blue), a perceptron layer with one neuron (blue), and a probabilistic layer (red).
11. Forecasting neural networks
Forecasting applications usually predict a continuous variable. In this case, they might require a scaling layer, a long-short term memory layer, a perceptron layer, an unscaling layer, and a bounding layer.
The following figure is a 1-day ahead forecasting model for the levels of NO2 in a city.
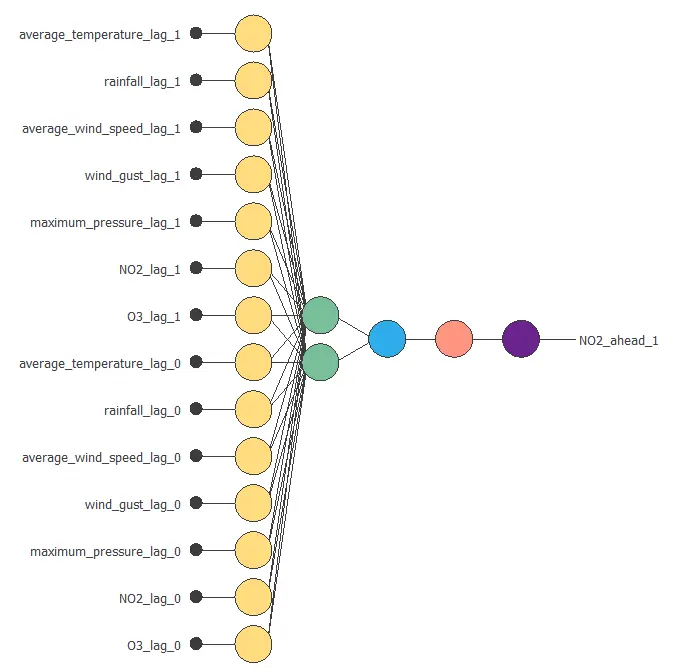
The above neural network has 14 inputs and one output. It consists of a scaling layer (yellow), an LSTM layer with two neurons (green), a perceptron layer with one neuron (blue), an unscaling layer (red), and a bounding layer (blue).
In all cases, the inputs will contain lags variables, and the outputs will have steps ahead variables.
Training Strategy ⇒
