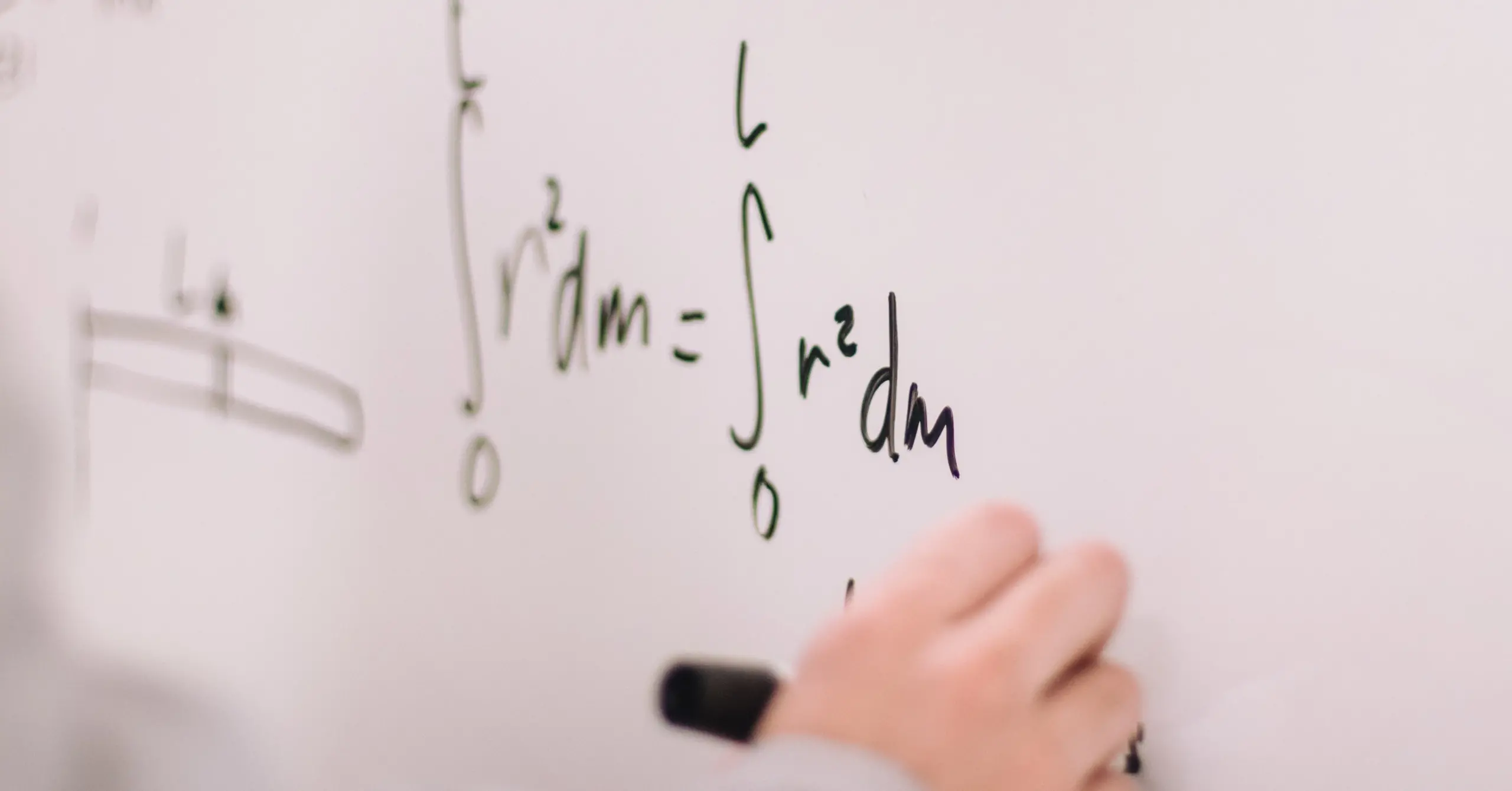The training algorithms orchestrates the learning process in a neural network, while the optimization algorithm (or optimizer) fine-tunes the model’s parameters during this training.
There are many different optimization algorithms. They are different regarding memory requirements, processing speed, and numerical precision.
This post first formulates the learning problem for neural networks. Then, it describes some essential optimization algorithms. Finally, it compares those algorithms’ memory, speed, and precision.
- Learning problem.
- 1. Gradient descent.
- 2. Newton method.
- 3. Conjugate gradient.
- 4. Quasi-Newton method.
- 5. Levenberg-Marquardt algorithm.
- Performance comparison.
- Conclusions.
Neural Designer includes many different optimization algorithms. This allows you to always get the best models from your data. You can download a free trial here.
Learning problem
The learning problem is formulated as minimizing a loss index (f). It is a function that measures the performance of a neural network on a data set.
The loss index includes, in general, an error and regularization terms. The error term evaluates how a neural network fits the data set. The regularization term prevents overfitting by controlling the model’s complexity.
The loss function depends on the neural network’s adaptative parameters (biases and synaptic weights). We can group them into a single n-dimensional weight vector $(\mathbf{w})$.
The following figure represents the loss function $(f(\mathbf{w}))$.
As we can see, the minimum of the loss function occurs at the point $(\mathbf{w}^{*})$. At any point (A), we can calculate the first and second derivatives of the loss function.
The gradient vector groups the first derivatives,
$$\nabla_i f(\mathbf{w}) = \frac{\partial f}{\partial w_{i}}$$
for $( i = 1,\ldots,n )$.
Similarly, the Hessian matrix groups the second derivatives,
$$\mathbf{H}_{i,j} f(\mathbf{w}) = \frac{\partial^{2} f}{\partial w_{i}\partial w_{j}},$$
for $( i,j = 0,1,\ldots )$.
The problem of minimizing continuous and differentiable functions of many variables is widely studied. We can directly apply many conventional approaches to this problem to training neural networks.
One-dimensional optimization
Although the loss function depends on many parameters, one-dimensional optimization methods are essential here.
Indeed, they are very often used in the training process of a neural network.
Many training algorithms first compute a training direction $(\mathbf{d})$ and then a training rate $(\eta)$ that minimizes the loss in that direction, $(f(\eta))$. The following figure illustrates this one-dimensional function.
The points $(\eta_1)$ and $(\eta_2)$ define an interval that contains the minimum of $(f)$, $(\eta^{*})$.
In this regard, one-dimensional optimization methods search for the minimum of one-dimensional functions. Some of the most used are the golden section and Brent’s method. Both reduce the minimum bracket until the distance between the outer points is less than a defined tolerance.
Multidimensional optimization
The learning problem for neural networks is formulated as searching for a parameter vector $(w^{*})$ at which the loss function $(f)$ takes a minimum value. The necessary condition states that if the neural network is at a minimum of the loss function, then the gradient is the zero vector.
The loss function is generally a non-linear function of the parameters. Consequently, it is impossible to find closed training algorithms for the minima. Instead, we consider a several-step search through the parameter space. The loss will decrease at each step by adjusting the neural network parameters.
In this way, to train a neural network, we start with some parameter vector (often chosen at random). Then, we generate a sequence of parameters to reduce the loss function at each algorithm iteration. The change of loss between two steps is called the loss decrement. The training algorithm stops when a specified condition, or stopping criterion, is satisfied.
1. Gradient descent (GD)
Gradient descent is the most straightforward training algorithm. It requires information from the gradient vector and is a first-order method.
Let denote $(f(\mathbf{w}^{(i)})=f^{(i)})$ and $(\nabla f(\mathbf{w}^{(i)})=\mathbf{g}^{(i)})$. The method begins at a point $(\mathbf{w}^{(0)})$ and, until a stopping criterion is satisfied, moves from $(\mathbf{w}^{(i)})$ to $(\mathbf{w}^{(i+1)})$ in the training direction $(\mathbf{d}^{(i)}=-\mathbf{g}^{(i)})$. Therefore, the gradient descent method iterates in the following way:
$$w^{(i+1)} = w^{(i)} – \mathbf{g}^{(i)}\eta^{(i)}, $$
for $( i = 0,1,\ldots )$.
The parameter (eta) is the training rate. This value can be set to a fixed value or found by one-dimensional optimization along the training direction at each step. An optimal value for the training rate obtained by line minimization at each successive step is generally preferable. However, many software tools still use only a fixed value for the training rate.
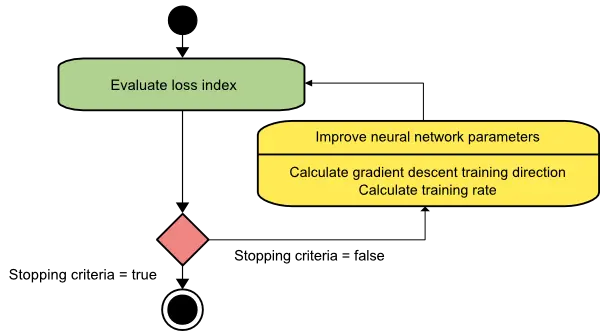
The following picture is an activity diagram of the training process with gradient descent. As we can see, the algorithm improves the parameters in two steps: First, it computes the gradient descent training direction. Second, it finds a suitable training rate.
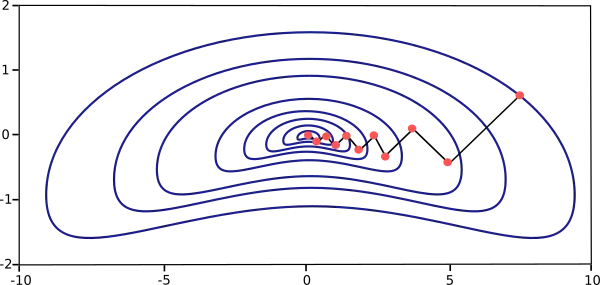
The gradient descent training algorithm has the severe drawback of requiring many iterations for functions that have long, narrow valley structures. Indeed, the downhill gradient is the direction in which the loss function decreases rapidly, but this does not necessarily produce the fastest convergence. The following picture illustrates this issue.
Gradient descent is the recommended algorithm for massive neural networks with many thousand parameters. The reason is that this method only stores the gradient vector $(size (n))$, and it does not keep the Hessian matrix of size $(size (n^{2}))$.
2. Newton’s method (NM)
Newton’s method is a second-order algorithm because it uses the Hessian matrix. This method aims to find better training directions by using the second derivatives of the loss function.
Let denote $(f(\mathbf{w}^{(i)})=f^{(i)})$, $(\nabla f(\mathbf{w}^{(i)})=\mathbf{g}^{(i)})$ and $(\mathbf{H} f(\mathbf{w}^{(i)})=\mathbf{H}^{(i)}).$ Consider the quadratic approximation of (f) at $(\mathbf{w}^{(0)})$ using the Taylor’s series expansion
$$ f = f^{(0)} + g^{(0)} \cdot(\mathbf{w} – \mathbf{w}^{(0)}) + 0.5\cdot(\mathbf{w} – \mathbf{w}^{(0)})^{2}\cdot \mathbf{H}^{(0)} $$
$(\mathbf{H}^{(0)})$ is the Hessian matrix of $(f)$ evaluated at the point $(\mathbf{w}^{(0)})$. By setting $(g)$ equal to $(0)$ for the minimum of $(f(\mathbf{w}))$, we obtain the next equation
$$ g = g^{(0)} + \mathbf{H}^{(0)}\cdot(\mathbf{w} – \mathbf{w}^{(0)}) = 0 $$
Therefore, starting from a parameter vector $(\mathbf{w}^{(0)})$, Newton’s method iterates as follows:
$$ \mathbf{w}^{(i+1)}=\mathbf{w}^{(i)}-\mathbf{H}^{(i)-1}\cdot \mathbf{g}^{(i)} $$
for $( i = 0,1,\ldots )$.
The vector $(\mathbf{H}^{(i)-1} \cdot \mathbf{g}^{(i)})$ is known as Newton’s step. Note that this parameter change may move towards a maximum rather than a minimum. This occurs if the Hessian matrix is not positive definite. Thus, Newton’s method does not guarantee to reduce the loss index at each iteration. To prevent that, Newton’s method equation is usually modified as follows:
$$ \mathbf{w}^{(i+1)}=\mathbf{w}^{(i)}-(\mathbf{H}^{(i)-1}\cdot \mathbf{g}^{(i)})\eta $$ for $( i = 0,1,\ldots )$.
The training rate, (eta) can either be set to a fixed value or found by line minimization. The vector $(\mathbf{d}^{(i)}=\mathbf{H}^{(i)-1}\cdot \mathbf{g}^{(i)})$ is now called Newton’s training direction.
The following figure depicts the state diagram for the training process with Newton’s method. The parameters are improved by obtaining a suitable training direction and rate.
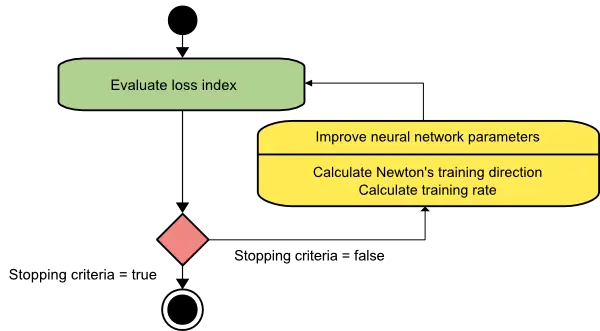
The picture below illustrates the performance of this method. As we can see, Newton’s method requires fewer steps than gradient descent to find the minimum value of the loss function.
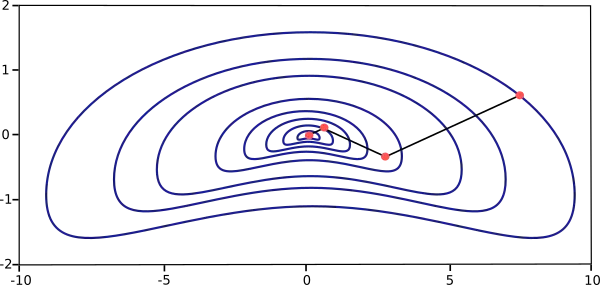
However, Newton’s method is complicated because the exact evaluation of the Hessian and its inverse are pretty expensive in computational terms.
3. Conjugate gradient (CG)
The conjugate gradient method can be regarded as an intermediate between gradient descent and Newton’s method.
It is motivated to accelerate the typically slow convergence associated with gradient descent. This method also avoids the information requirements related to the Hessian matrix’s storage, evaluation, and inversion, as Newton’s method requires.
In the conjugate gradient training algorithm, the search is performed along with conjugate directions. They generally produce faster convergence than gradient descent directions. These training directions are conjugated concerning the Hessian matrix.
Let denote d as the training direction vector. Then, starting with an initial parameter vector $(\mathbf{w}^{(0)})$ and an initial training direction vector $(\mathbf{d}^{(0)}=-\mathbf{g}^{(0)})$, the conjugate gradient method constructs a sequence of training directions as:
$$ \mathbf{d}^{(i+1)}=\mathbf{g}^{(i+1)}+\mathbf{d}^{(i)}\cdot \gamma^{(i)}, $$
for $( i = 0,1,\ldots )$.
Here, $(\gamma)$ is called the conjugate parameter, and there are different ways to calculate it. Two of the most used are Fletcher and Reeves and Polak and Ribiere. For all conjugate gradient algorithms, the training direction is periodically reset to the negative of the gradient.
The parameters are then improved according to the following expression.
$$ \mathbf{w}^{(i+1)}=\mathbf{w}^{(i)}+\mathbf{d}^{(i)}\cdot \eta^{(i)} $$
for $( i = 0,1,\ldots )$.
The training rate, $(\eta)$, is usually found by line minimization.
The picture below depicts an activity diagram for the training process with the conjugate gradient. Here, the improvement of the parameters is done in two steps. First, the algorithm computes the conjugate gradient training direction. Second, it finds a suitable training rate in that direction.
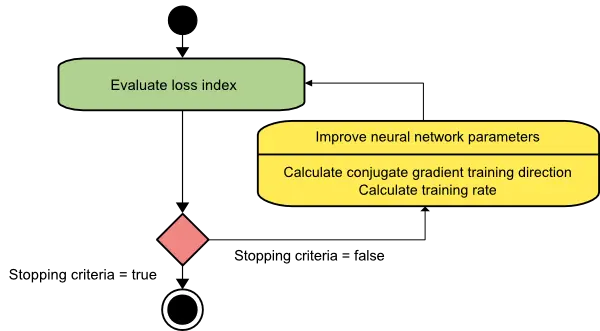
This method has proved more effective than gradient descent in training neural networks. Since it does not require the Hessian matrix, the conjugate gradient also performs well with vast neural networks.
4. Quasi-Newton method (QNM)
The application of Newton’s method is computationally expensive. Indeed, it requires many operations to evaluate the Hessian matrix and compute its inverse. Alternative approaches, known as quasi-Newton, are developed to solve that drawback. These methods do not calculate the Hessian directly and then evaluate its inverse. Instead, they build up an approximation to the inverse Hessian. This approximation is computed using only information on the first derivatives of the loss function.
The Hessian matrix comprises the second partial derivatives of the loss function. Thus, the main idea behind the quasi-Newton method is approximating the inverse Hessian by another matrix $(\mathbf{G})$, using only the first partial derivatives of the loss function. Then, the quasi-Newton formula is expressed as
$$ \mathbf{w}^{(i+1)}=\mathbf{w}^{(i)}-(\mathbf{G}^{(i)}\cdot \mathbf{g}^{(i)})\cdot\eta^{(i)} $$
for $( i = 0,1,\ldots )$.
The training rate (eta) can be set to a fixed value or be found by line minimization. The inverse Hessian approximation $(\mathbf{G})$ has different flavors. Two of the most used ones are the Davidon–Fletcher–Powell (DFP) and the Broyden–Fletcher–Goldfarb–Shanno (BFGS) formulas.
The activity diagram of the quasi-Newton training process is illustrated below. Improvement of the parameters is performed in two steps. First, the algorithms obtain the quasi-Newton training direction. Second, it finds a satisfactory training rate. This is the default method to use in most cases:
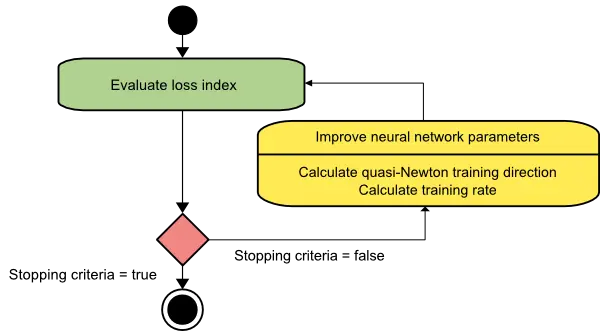
It is faster than gradient descent and conjugate gradient, and the exact Hessian must not be computed and inverted.
5. Levenberg-Marquardt algorithm (LM)
The Levenberg-Marquardt algorithm is designed to work specifically with loss functions defined by a sum of squared errors. It works without computing the exact Hessian matrix. Instead, it works with the gradient vector and the Jacobian matrix.
Consider a loss function which takes the form of a sum of squared errors,
$$ f = \sum_{i=1}^{m} e_{i}^{2} $$
Here $(m)$ is the number of training samples.
We can define the Jacobian matrix of the loss function as that containing the derivatives of the errors concerning the parameters,
$$ \mathbf{J}_{i,j} = \frac{\partial e_{i}}{\partial \mathbf{w}_{j}}, $$
for $( i=1,\ldots,m )$ and $( j = 1,\ldots,n )$.
Where $(m)$ is the number of samples in the data set, and (n) is the number of parameters in the neural network.
Note that the size of the Jacobian matrix is $(m\cdot n)$.
We can compute the gradient vector of the loss function as
$$\nabla f = 2 \mathbf{J}^{T}\cdot \mathbf{e}$$
Here $(\mathbf{e})$ is the vector of all error terms.
Finally, we can approximate the Hessian matrix with the following expression.
$$\mathbf{H} f \approx 2 \mathbf{J}^{T}\cdot \mathbf{J} + \lambda \mathbf{I}$$
Where $(\lambda)$ is a damping factor that ensures the positiveness of the Hessian and $(I)$ is the identity matrix.
The next expression defines the parameters improvement process with the Levenberg-Marquardt algorithm
$$ \mathbf{w}^{(i+1)}=\mathbf{w}^{(i)}
– (\mathbf{J}^{(i)T}\cdot \mathbf{J}^{(i)}+ \lambda^{(i)}\mathbf{I})^{-1} \cdot (2\mathbf{J}^{(i)T}\cdot \mathbf{e}^{(i)}), $$
for $( i = 0,1,\ldots )$.
Newton’s method uses the approximate Hessian matrix when the damping parameter $(\lambda)$ is zero. On the other hand, when $(\lambda)$ is large, this becomes a gradient descent with a small training rate.
The parameter $(\lambda)$ is initialized to be large, so the first updates are small steps in the gradient descent direction.
If any iteration results in a fail, then $(\lambda)$ is increased by some factor. Otherwise, $(\lambda)$ is reduced as the loss decreases, so the Levenberg-Marquardt algorithm approaches the Newton method. This process typically accelerates the convergence to the minimum.
The picture below represents a state diagram for the training process of a neural network with the Levenberg-Marquardt algorithm. The first step is calculating the loss, the gradient, and the Hessian approximation. Then, the damping parameter is adjusted to reduce the loss at each iteration.
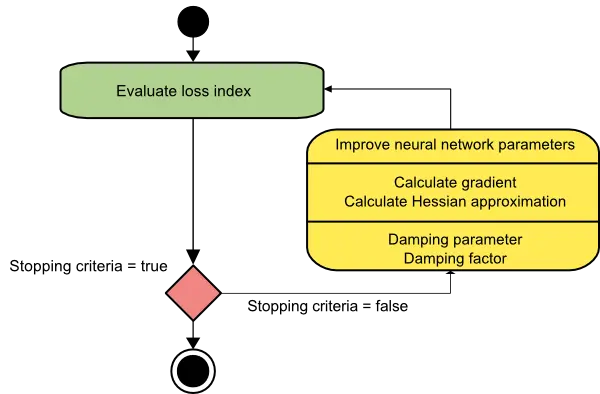
As we have seen, the Levenberg-Marquardt algorithm is tailored for the sum-of-squared error functions.
That makes it very fast when training neural networks measured on that error.
However, this algorithm has some drawbacks. First, it cannot minimize functions such as the root mean squared error or the cross-entropy error. Also, the Jacobian matrix becomes enormous for big data sets and neural networks, requiring much memory. Therefore, the Levenberg-Marquardt algorithm is not recommended for big data sets or neural networks.
Performance comparison
The following chart depicts the computational speed and the memory requirements of the training algorithms discussed in this post.
As we can see, the slowest training algorithm is usually gradient descent, but it is the one requiring less memory.
On the contrary, the fastest one might be the Levenberg-Marquardt algorithm, but it usually requires much memory.
A good compromise might be the quasi-Newton method.
Conclusions
If our neural network has thousands of parameters, we can use gradient descent or conjugate gradient to save memory.
If we have many neural networks to train with just a few thousand samples and a few hundred parameters, the best choice might be the Levenberg-Marquardt algorithm.
In the rest of the situations, the quasi-Newton method will work well.
Neural Designer implements all those optimization algorithms. You can download the free trial to see how they work in practice.