Acquiring a new client is far more expensive than keeping an existing one.
Understanding why customers leave helps companies act before churn happens.
Churn prevention supports targeted loyalty programs and retention campaigns.
In this example, we use bank customer data to build a churn prediction model.
We develop the model with Neural Designer, an explainable machine learning platform.
You can follow the process step by step using the free trial.
Contents
1. Application type
The variable to be predicted is binary (churn or loyal). Therefore, this is a classification project.
The goal here is to model churn probability conditioned on the customer features.
2. Data set
The data set contains information for creating our model. We need to configure three things here:
- Data source.
- Variables.
- Instances.
Data source
The data file bank_churn.csv contains 12 features about 10000 clients of the bank.
Variables
The features or variables are the following:
Identification
Customer ID: Unique identifier of the client (unused variable).
Demographics
- Country: Client’s country of residence.
- Gender: Client’s gender.
- Age: Client’s age.
Banking Relationship
- Tenure: Number of years the client has been with the bank.
- Balance: Account balance of the client.
- Products number: Number of bank products held by the client.
- Credit card: Indicates whether the client has a credit card (yes/no).
- Active member: Indicates whether the client is considered an active customer.
Financial Information
- Credit score: Creditworthiness rating of the client.
- Estimated salary: Estimated annual salary of the client.
Target Variable
Churn: 1 if the client left the bank during the period, 0 if they remained.
Instances
On the other hand, the instances are randomly split into training (60%), selection (20%), and testing (20%) subsets.
Distributions
Once the variables and instances are configured, we can perform some analytics on the data.
The data distributions tell us the percentages of churn and loyal customers.
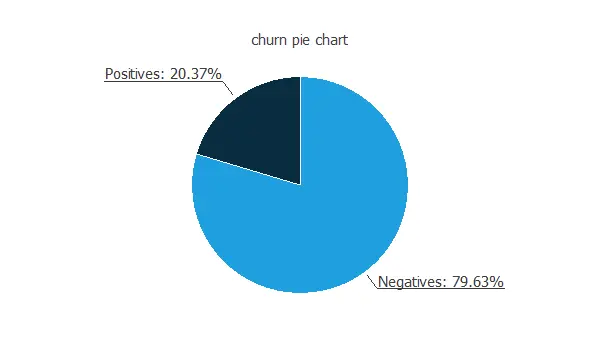
In this dataset, the percentage of churn customers is about 20%.
Input-target correlations
The input-target correlations might indicate which variables might be causing attrition.
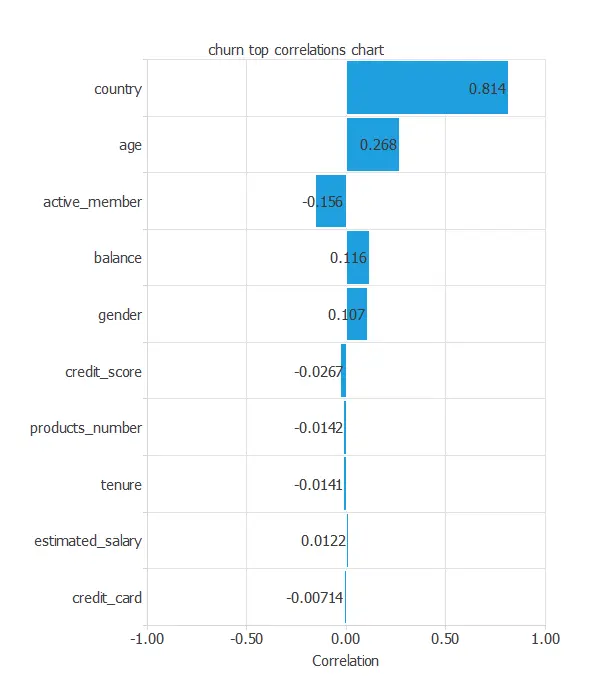
The above chart shows that the country has a significant influence and that older customers are more likely to leave the bank.
3. Neural network
The second step is to choose a neural network to represent the classification function. Classification models usually contain the following layers:
Scaling layer
For the scaling layer, the minimum and maximum scaling methods are set.
Hidden dense layer
We set one perceptron layer, with 3 neurons as a first guess, having the logistic activation function.
Output dense layer
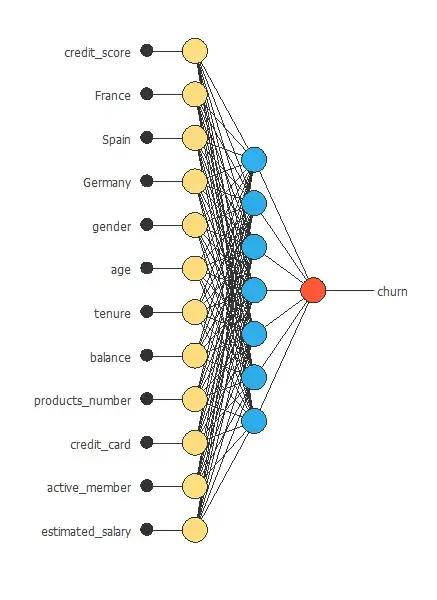
The following figure is a diagram of the neural network used in this example.
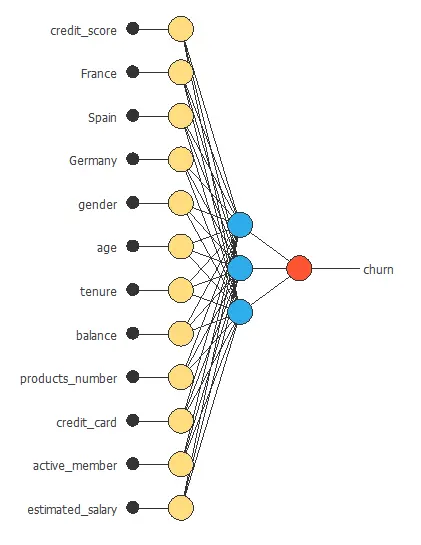
4. Training strategy
The training strategy is applied to the neural network to obtain the best possible performance. It is composed of two things:
- A loss index.
- An optimization algorithm.
Loss index
The selected loss index is the weighted squared error with L2 regularization. The weighted squared error is helpful in applications where the targets are unbalanced. It gives a weight of 3.91 to churn customers and 1 to loyal customers.
Optimization algorithm
The selected optimization algorithm is the quasi-Newton method.
Training
The following chart shows how the training (blue) and selection (orange) errors decrease with the training epochs.
The final errors are 0.621 WSE for training and 0.656 WSE for validation.
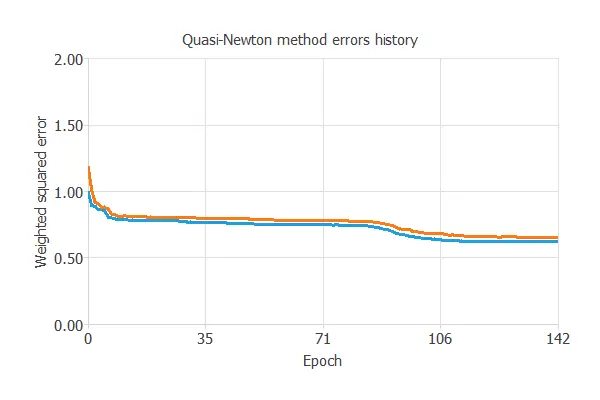
The following section will improve the generalization performance by reducing the selection error.
5. Model selection
Input selection (or feature selection) searches for the inputs that produce the best generalization.
Order selection searches for the complexity of the neural network that optimizes the generalization performance.
The following chart shows each order’s training and selection errors after performing the incremental order method.
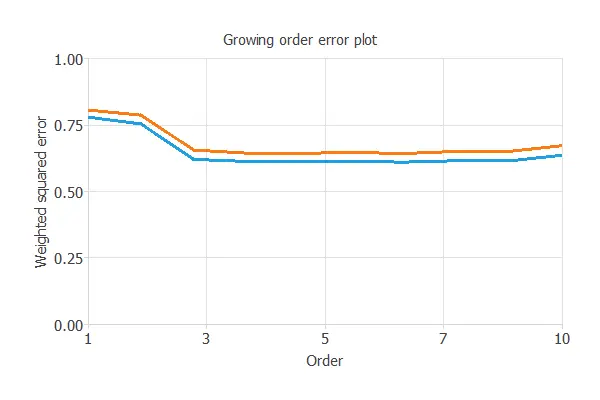
The chart shows that the optimal number of neurons is 6, with selection error = 0.643.
The following figure shows the final network architecture for this application.
6. Testing analysis
The next step is to perform an exhaustive testing analysis to validate the neural network’s predictive capabilities.
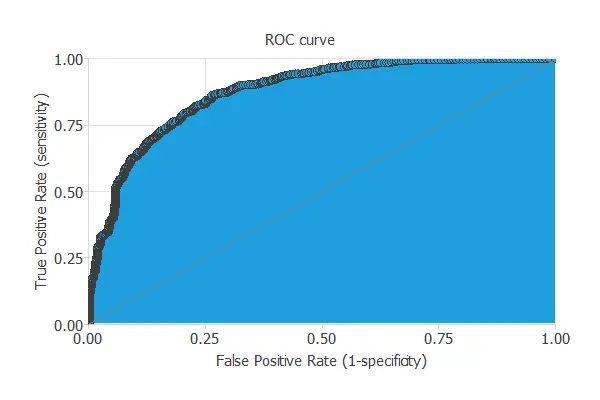
ROC curve
The ROC curve is a common way to measure the precision of a binary classifier.
Its primary metric is the area under the curve (AUC), which is 0.5 for random guessing and 1 for a perfect model.
Our model achieved an AUC of 0.874, indicating excellent performance.
Confusion matrix
We can also examine the confusion matrix. Next, we show the elements of this matrix for a decision threshold = 0.5.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 305 (15%) | 80 (4%) |
| Real negative | 344 (17%) | 1271 (63%) |
Binary classification metrics
From the above confusion matrix, we can calculate the following binary classification tests:
- Accuracy: 78.8% (ratio of correctly classified samples).
- Error: 21.2% (ratio of misclassified samples).
- Sensitivity: 79.2% (percentage of actual positives classified as positive).
- Specificity: 78.7% (percentage of actual negatives classified as negative).
Cumulative gain
Now we can simulate a retention campaign’s performance using the cumulative gain chart.
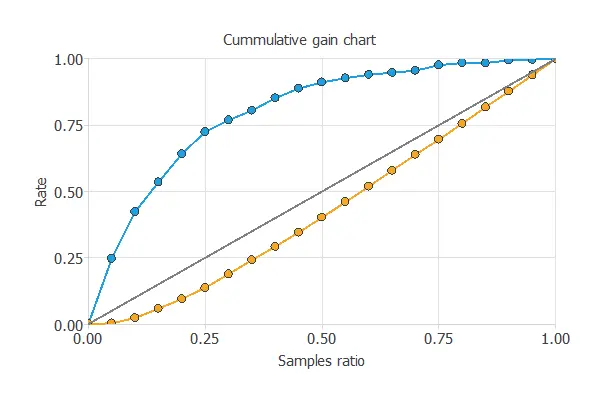
The above chart indicates that contacting 25% of the customers most likely to churn will reach 75% of those leaving the bank.
7. Model deployment
Once we have tested the churn model, we can use it to evaluate the probability of our customers’ churning.
Neural network outputs
For instance, consider a customer with the following features:
- credit_score: 650
- country: France
- gender: Female
- age: 39
- tenure: 5
- balance: 76485
- products_number: 2
- credit_card: Yes
- active_member: No
- estimated_salary: 100000
The probability of churn for that customer is 38%.
Conclusions
This example uses customer data from a bank to build a machine learning model to predict the probability of client churn.
