The objective is to design a machine learning model that accurately detects gamma rays and distinguishes them from the background.
The Cherenkov telescope uses the atmosphere as the detector.
Gamma rays create air showers that emit Cherenkov light.
The camera records this light as a “rain image.”
These images let us distinguish gamma events (signal) from hadronic showers (background).
We use Hillas parameters, along with features like energy asymmetry, cluster extent, and total signal, for discrimination.
Contents
1. Application type
This is a classification project since the variable to be predicted is binary: gamma (signal) or hadron (background).
2. Data set
The first step is to prepare the dataset, which serves as the source of information for the classification problem.
For that, we need to configure the following concepts:
- Data source.
- Variables.
- Instances.
Data source
The data source is the file gamma.csv. It contains the data for this example in comma-separated values (CSV) format. The number of columns is 11, and the number of rows is 19020.
The CORSIKA simulation program generated the data set, utilizing a Monte Carlo code to simulate extensive air showers.
Additionally, it has been utilized to simulate the registration of high-energy gamma particles from the Cherenkov gamma telescope using the imaging technique.
Variables
The variables are:
Shape features
- length – Major axis of the ellipse (mm).
- width – Minor axis of the ellipse (mm).
- M3Long – Cube root of the third moment along the major axis (mm).
- M3Trans – Cube root of the third moment along the minor axis (mm).
Intensity/concentration features
- size – Log of total pixel content (photons).
- conc – Ratio of the two highest pixel sums to total size.
- conc1 – Ratio of the highest pixel to total size.
Geometry and orientation features
- asym – Distance from highest pixel to center, projected on major axis (mm).
- alpha – Angle of the ellipse’s major axis relative to the origin vector (°).
- distance – Distance from the origin to the ellipse center (mm).
Target variable
- class – Event type: gamma (signal) or hadron (background).
Instances
Neural Designer randomly splits the instances into 60% training (11,412), 20% validation (3,804), and 20% testing (3,804).
Variables distributions
We can calculate the distributions of all variables. The following figure is the pie chart for the gamma or hadron cases.
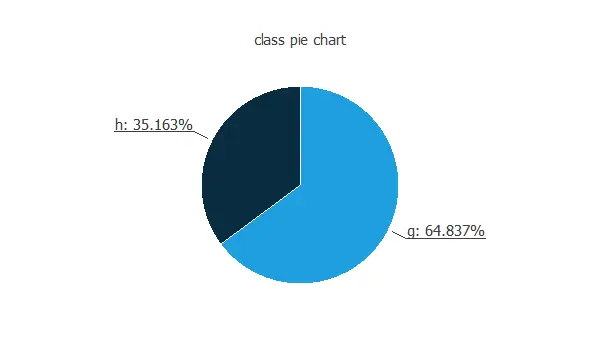
As we can see, most of the samples are gamma signals. The hadron class (background) represents the majority of events in the actual data.
Input-target correlations
Finally, the input-target correlations might indicate to us what factors most influence.
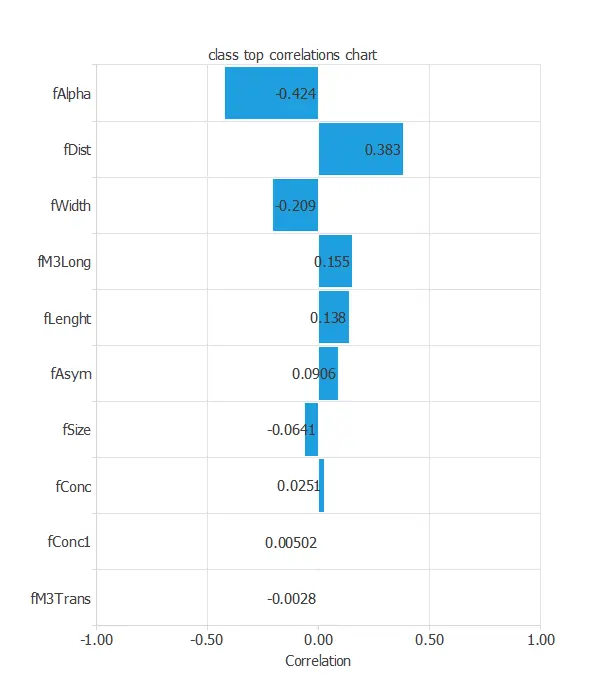
The most correlated variables with the classification are alpha and dist, which refer to ellipse variables.
Additionally, there are not many correlated variables, such as fConc1 and fM3Trans.
3. Neural network
The second step is to choose a neural network. In classification problems, it is usually composed of:
- A scaling layer.
- Two perceptron layers.
- A probabilistic layer.
Scaling layer
The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables.
Hidden dense layer
The number of perceptron layers is 1. This perceptron layer has 10 inputs and 10 neurons.
Output dense layer
Finally, we will set the binary probabilistic method for the probabilistic layer, as we want the predicted target variable to be binary.
Neural network graph
The following figure is a graphical representation of this classification neural network.
In this diagram, yellow circles are scaling neurons, blue circles are perceptron neurons, and red circles are probabilistic neurons.
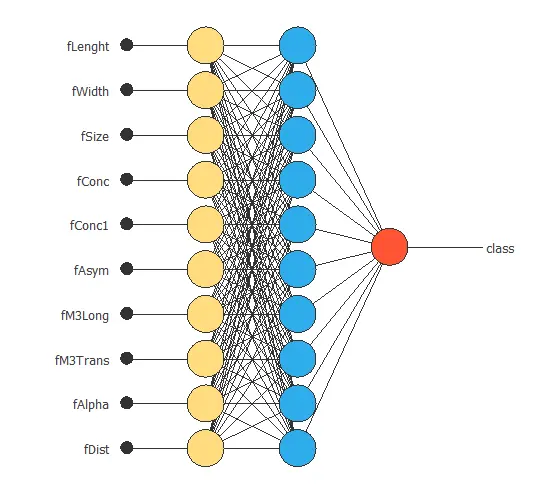
The number of inputs is 10, and the number of outputs is 1.
4. Training strategy
The fourth step is to set the training strategy, which is composed of:
- Loss index.
- Optimization algorithm.
Loss index
The loss index chosen for this application is the normalized squared error with L2 regularization.
The error term trains the neural network using the training instances of the dataset.
The regularization term makes the model more stable and improves generalization.
Optimization algorithm
The optimization algorithm searches for the neural network parameters that minimize the loss index.
The quasi-Newton method is chosen here.
Training
The following chart illustrates how the training and selection errors decrease over the course of training epochs.
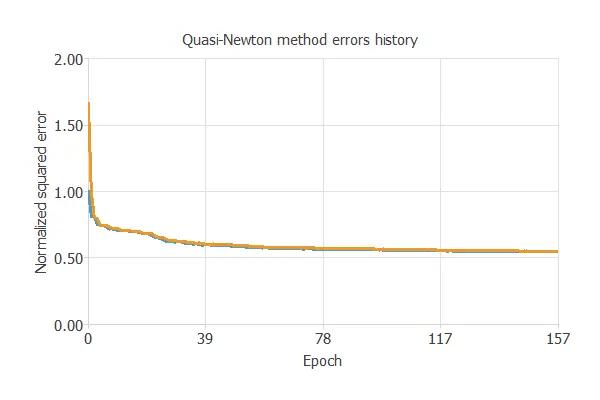
The final values are training error = 0.547 NSE (blue) and selection error = 0.550 NSE (orange).
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties, which minimizes the error on the selected instances of the data set.
More specifically, we aim to develop a neural network with a selection error of less than 0.550 WSE, the value we have previously achieved.
Order selection algorithms train several network architectures with different numbers of neurons and select the one with the smallest selection error.
The incremental order method starts with a few neurons and increases the complexity at each iteration.
6. Testing analysis
The last step is to test the neural network’s generalization by comparing its predicted values with the observed ones.
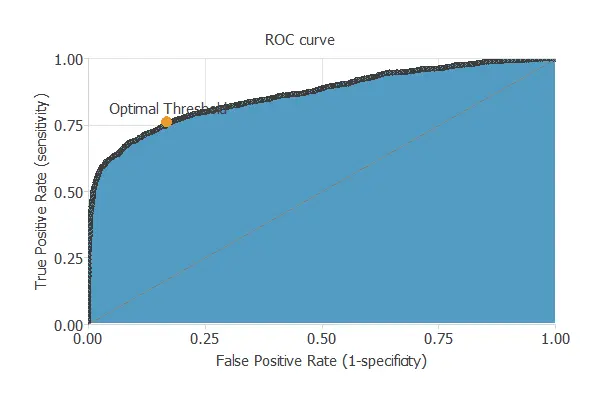
ROC curve
We can use the ROC curve as it is the standard testing method for binary classification projects.
Confusion matrix
In the confusion matrix, rows are the actual values and columns are the predicted values.
Diagonal cells show correct classifications, while off-diagonal cells show errors.
| Predicted positive (gamma) | Predicted negative (background) | |
|---|---|---|
| Real positive (gamma) | 2120 (55.8%) | 283 (7.4%) |
| Real negative (background) | 407 (10.7%) | 993 (26.1%) |
As we can see, the model correctly predicts 3114 instances (81.9%), while misclassifying 690 (18.1%).
This indicates that our predictive model achieves high classification accuracy.
Binary classification metrics
The following list depicts the binary classification tests for this application:
- Classification accuracy: 81.9% (percentage of correctly classified samples).
- Error rate: 18.1% (percentage of misclassified samples).
- Sensitivity: 88.2% (percentage of actual positives classified as positive).
- Specificity: 70.9% (percentage of actual negatives classified as negative).
7. Model deployment
The neural network is now ready to predict outputs for inputs it has never seen. This process is called model deployment.
Neural network outputs
We calculate the neural network outputs from the different variables to classify a given signal. For instance:
- lenght: 341.4 mm.
- width: 190.3 mm.
- size: 25.7 phot.
- conc: 0.4.
- conc1: 0.2.
- asym: 24.4 mm.
- M3Long: 118.4 mm.
- M3Trans: 1.5 mm.
- alpha: 182.6 degrees.
- dist: 225.2 mm.
- Probability of signal gamma: 80%.
The neural network would classify the signal as a gamma-ray signal for this case.
Conclusions
We have just built a predictive model to determine whether the measured data originates from gamma rays or from the hadron shower, which we consider as background.
References
- The data for this problem has been taken from the UCI Machine Learning Repository.
- Bock, R.K., Chilingarian, A., Gaug, M., Hakl, F., Hengstebeck, T., Jirina, M., Klaschka, J., Kotrc, E., Savicky, P., Towers, S., Vaicilius, A., Wittek W. (2004). Methods for multidimensional event classification: a case study using images from a Cherenkov gamma-ray telescope. Nucl.Instr.Meth. A, 516, pp. 511-528.
- P. Savicky, E. Kotrc. Experimental Study of Leaf Confidences for Random Forest. Proceedings of COMPSTAT 2004, In: Computational Statistics. (Ed.: Antoch J.) – Heidelberg, Physica Verlag 2004, pp. 1767-1774.
- J. Dvorak, P. Savicky. Softening Splits in Decision Trees Using Simulated Annealing. Proceedings of ICANNGA 2007, Warsaw, (Ed.: Beliczynski et. al), Part I, LNCS 4431, pp. 721-729.