This example aims to predict inflation from the macroeconomic data of a country using machine learning.
Inflation is the rate of increase in the cost of goods and services over a given period of time.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
We solve this example with the data science and machine learning platform Neural Designer.
To follow this example step by step, you can use the free trial.
1. Application type
This is a forecasting project since the variable to predict is the future inflation.
The goal is to model the inflation rate for the next month based on various macroeconomic features from the past three months.
2. Data set
The data set contains information to create our model. We need to configure three things:
- Data source.
- Variables.
- Instances.
Data source
The data file used for this example is macroeconomics.csv, which contains monthly information about 16 features for 19 years.
Variables
The data set includes the following variables:
Time
Date: Monthly data from January 2001 to November 2019.
Monetary Policy & Inflation
- Reference rate (NBP): Central Bank of Poland’s reference interest rate.
- Core inflation: Inflation rate excluding food and energy prices.
- Consumer Price Index (CPI): Measure of average changes in consumer prices.
- WIBOR 3M: Three-month Warsaw Interbank Offered Rate.
Labor Market
- Average monthly salary (enterprise sector): Growth rate of gross nominal wages in enterprises.
- Average employment (enterprise sector): Growth rate of employment in enterprises.
- Unemployment rate: Registered unemployment rate at the end of each month.
Industry & Production
- Sold production of industry: Growth rate of total industrial production sold.
- Price index of industry: Growth rate of the industrial production price index.
External Balance
Account balance: Poland’s current account balance (in million euros).
Exchange Rates
- EUR/PLN: Monthly average of daily closing exchange rates (euro to zloty).
- USD/PLN: Monthly average of daily closing exchange rates (US dollar to zloty).
- CHF/PLN: Monthly average of daily closing exchange rates (Swiss franc to zloty).
Stock Market
- WIG20: Monthly average of the Warsaw Stock Exchange index for the 20 largest companies.
- WIG: Monthly average of the Warsaw Stock Exchange main index.
Instances
On the other hand, the instances are divided sequentially into training, selection, and testing subsets, containing 60%, 20%, and 20% of the cases, respectively.
Inputs-targets correlations
We can calculate the input-target correlations. These indicate which macroeconomic factors have the most significant influence on inflation.
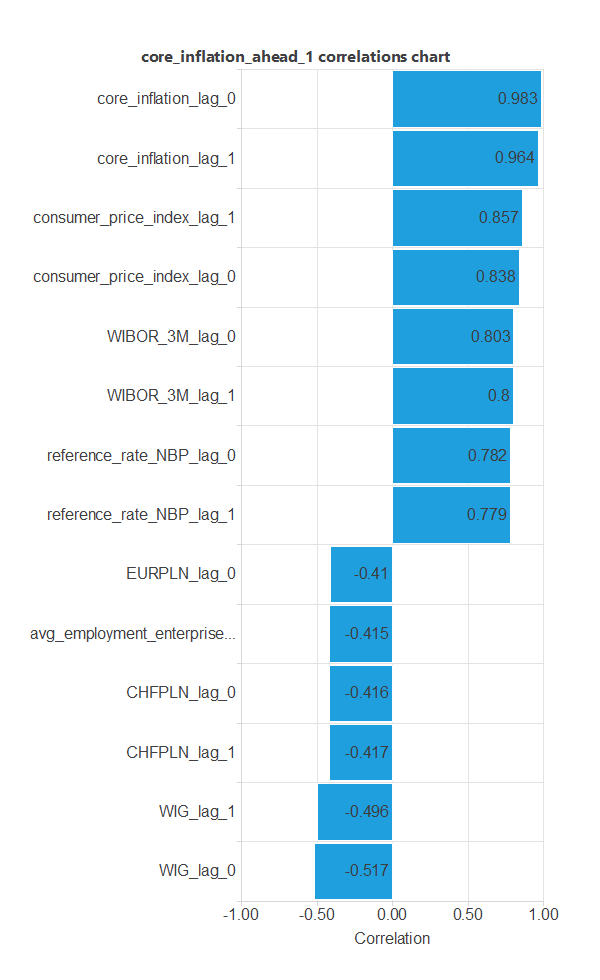
In this example, there are a few variables that correlate highly with the target variable. They are WIBOR_3M, consumer_price_index, and reference_rate_NBP.
Time series charts
We can also check the time series charts for these variables.
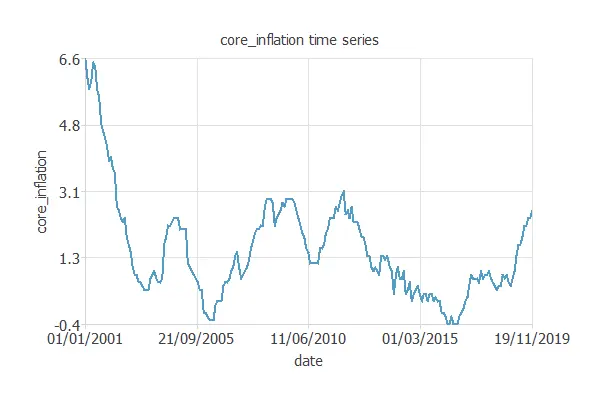
Looking at the time series plot for the target variable, we can see that core inflation has been in the same range for the past 15 years.
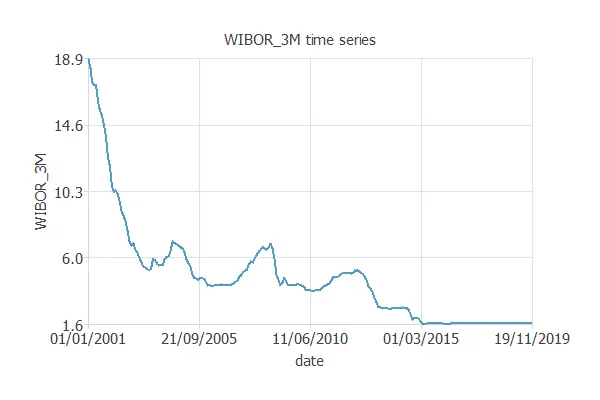
We can also look at the WIBOR_3M chart. If we compare the two previous plots, we see the correlation between the two variables.
3. Neural network
The next step is to set the neural network parameters. In our case, it is composed of:
- Scaling layer.
- Perceptron layer.
- Probabilistic layer.
We could have also used an LSTM layer.
The mean and standard deviation scaling method has been set for the scaling layer.
Next, we set one perceptron layer with 3 neurons that have the hyperbolic tangent activation function. This layer has 45 inputs, which are the 15 variables of the dataset for three months. The output is one, the core inflation for the next month.
Neural network graph
The neural network for this example can be represented with the following diagram:
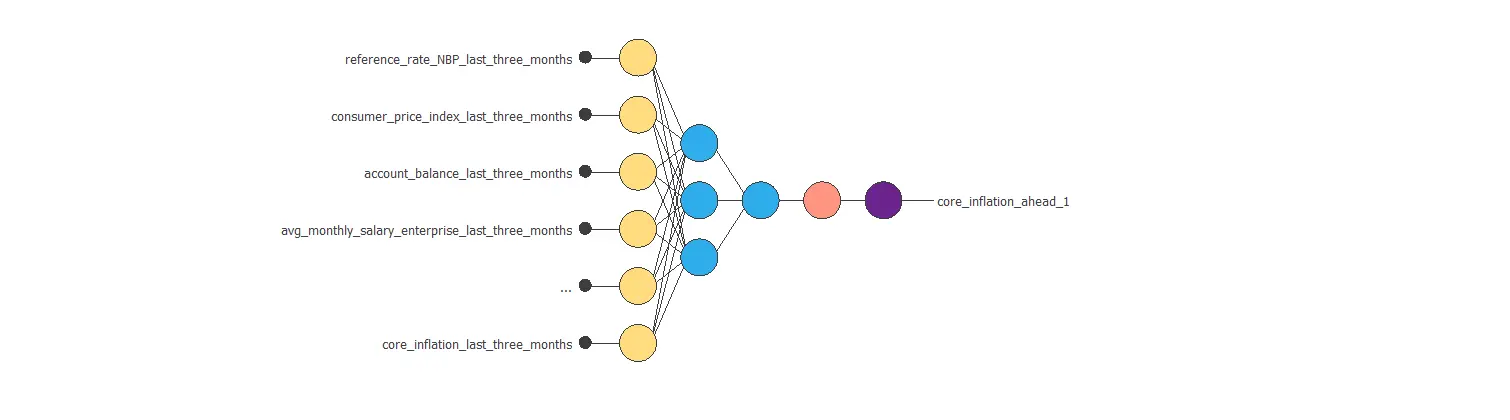
4. Training strategy
The fourth step is to set the training strategy, defining what the neural network will learn.
A general training strategy for classification is composed of two terms:
- A loss index.
- An optimization algorithm.
Loss index
The loss index chosen for this problem is the normalized squared error between the outputs from the neural network and the targets in the data set with L1 regularization.
Optimization algorithm
The selected optimization algorithm is the Quasi-Newton method.
Training
The following chart shows how the training error develops with the epochs during the training process.
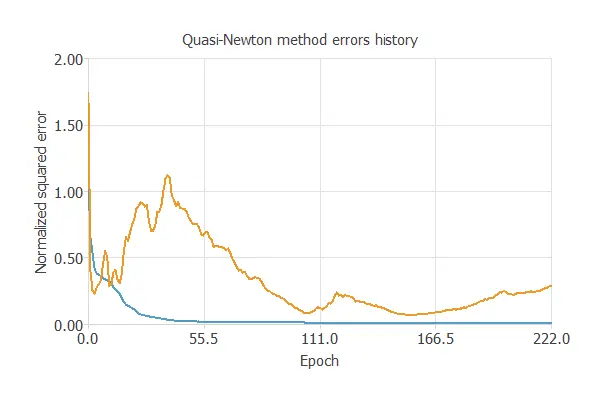
The final value is training error = 0.006 NSE and selection error = 0.289 NSE.
5. Model selection
The objective of model selection is to improve the neural network’s generalization capabilities or, in other words, to reduce the selection error.
First, we perform the neuron selection. We want a model whose complexity is the most appropriate to produce an adequate fit of the data. The optimal value for this example is one neuron.
Next, we will apply an input selection algorithm. This reduces our inputs to six: the consumer_price_index and the core_inflation for the past three months.
The resulting neural network is as follows.
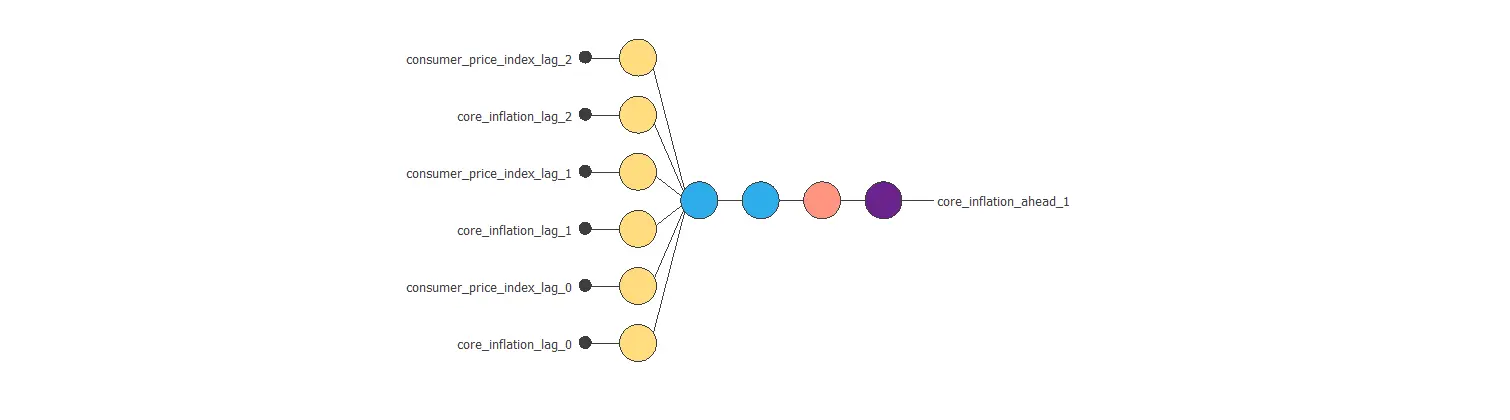
With it, the selection error decreases to 0.057 NSE. It is a significant improvement compared to the previous value.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network.
To validate a forecasting technique, we need to compare the values provided by this technique to the observed values.
Goodnes-of-fit
We can use linear regression analysis as the standard testing method for these projects.
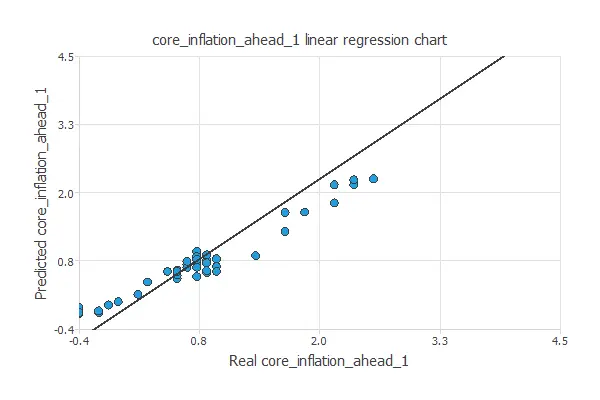
The correlation value for this example is R2 = 0.977, which is close to 1.
This means that we have a good predictive model.
Error statistics
We can also calculate the error statistics.
The mean absolute error obtained by using the previous value as the prediction is 0.320. Using the model, it lowers to 0.186.
Therefore, we are improving the prediction of the core inflation with respect to the baseline.
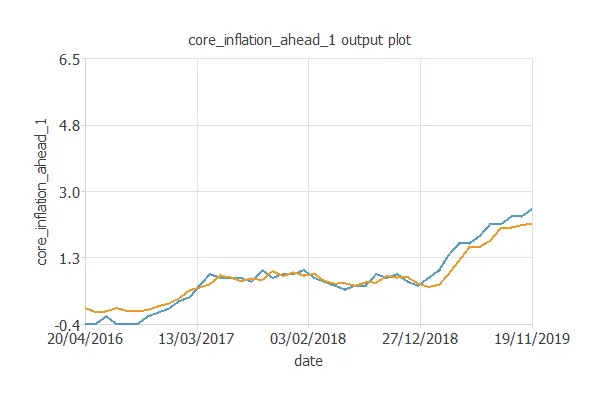
Output plot
The output plot shows the real values (blue) and the predicted values (orange) over time.
Conclusions
In this post, we have built a machine learning model to predict the inflation of a country.
References
- The data for this problem has been taken from Kaggle.


