In this example, we build a machine learning model to detect fraud in credit card transactions.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
- Tutorial video.
This example was solved with Neural Designer. You can use the free trial to follow this example step by step.
1. Application type
This is a classification project since the predictor variable is binary (fraudulent or not fraudulent).
The goal is to create a model to obtain the likelihood of a transaction being fraudulent.
2. Data set
The data set contains information to create our model. We need to configure three things:
- Data source.
- Variables.
- Instances.
The data file used for this example is creditcard-fraud.csv, which contains 11 features for about 3,075 payments.
Variables
The data set includes the following variables:
- merchant_id: id of the merchant.
- avg_amount_day: average of the amount per transaction per day.
- transaction_amount: the amount of the transaction.
- is_declined: yes = the credit card is declined, no = the credit card is not declined.
- number_declines_day: total number of declines per day.
- foreign_transaction: yes = it is a foreign transaction, no = it is not a foreing transaction.
- high_risk_country: yes = it is a high-risk country, no = it is not a high-risk country.
- daily_chbk_avg_amt: daily average of chargeback.
- 6m_avg_chbk_amt: 6-month average of chargeback.
- 6m_chbk_freq: frequency of the 6-month chargeback.
- is_fradulent: fraudulent = the payment is fraudulent, not-fraudulent = the payment is not fraudulent (target variable).
Instances
On the other hand, the instances are divided randomly into training, selection, and testing subsets, containing 60%, 20%, and 20% of the instances, respectively.
Variables distributions
Our target variable is is_fradulent. We can calculate the data distributions and plot a pie chart with the percentage of instances for each class.
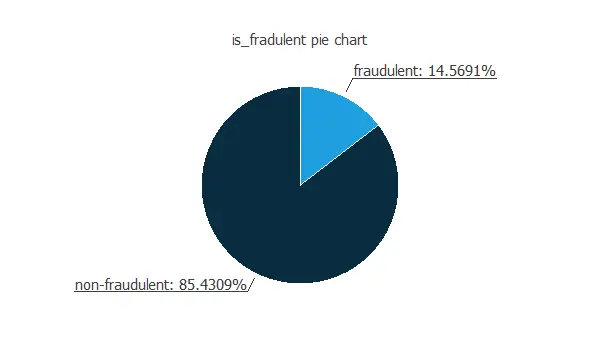
As we can see, the target variable is unbalanced since many payments are not fraudulent, around 85%, while only 15% are fraudulent. So we could say that about 1 out of 6 payments is fraudulent.
Inputs-targets correlations
The inputs-target correlations might indicate which factors have the most significant influence on a fraudulent transaction.
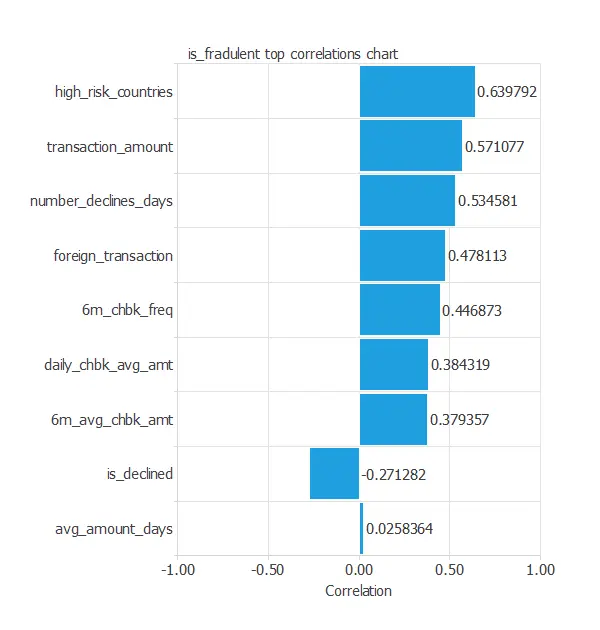
In this example, all variables have a positive correlation except for is_declined. Moreover, the variable high_risk_country has the highest correlation with the target variable.
3. Neural network
The next step is to set the neural network parameters. For classification problems, it is composed of:
- Scaling layer.
- Perceptron layers.
- Probabilistic layer.
We have set the mean and standard deviation scaling method for the scaling layer,
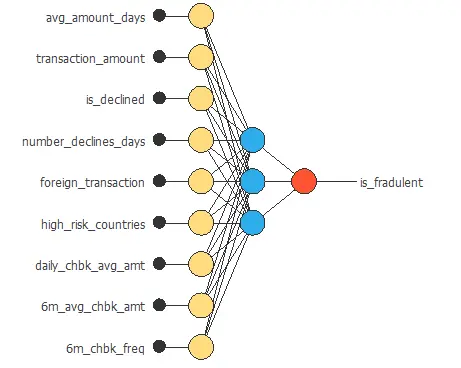
We set one perceptron layer with 3 neurons having the logistic activation function. This layer has nine inputs, and since the target variable is binary, only one output.
The neural network for this example can be represented with the following diagram:
4. Training strategy
The fourth step is to set the training strategy defining what the neural network will learn. A general training strategy for classification is composed of two terms:
- A loss index.
- An optimization algorithm.
The loss index chosen for this problem is the normalized squared error between the neural network’s outputs and the targets in the data set with L1 regularization.
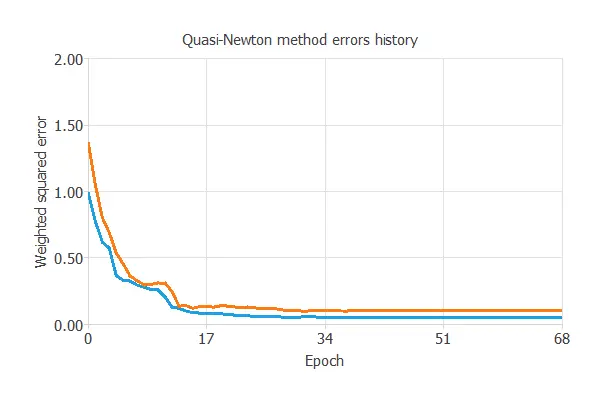
The selected optimization algorithm is the Quasi-Newton method. The selected optimization algorithm is the Quasi-Newton method.
The following chart shows how training and selection errors develop with the epochs during training. The final values are training error = 0.052 NSE and selection error = 0.103 NSE.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties, which means the one that minimizes the error on the selected instances of the data set.
More specifically, we want to find a neural network with a selection error smaller than 0.103 NSE, which is the value we have achieved.
Order selection algorithms train several network architectures with a different number of neurons and select the one with the smallest selection error.
The incremental order method starts with a few neurons and increases the complexity at each iteration. The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.
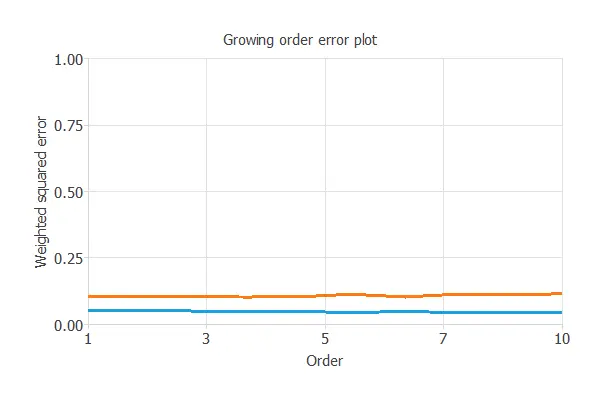
The selection errors achieved are similar for any number of variables; however, the smallest is 0.1007 for an optimal number of neurons of 4.
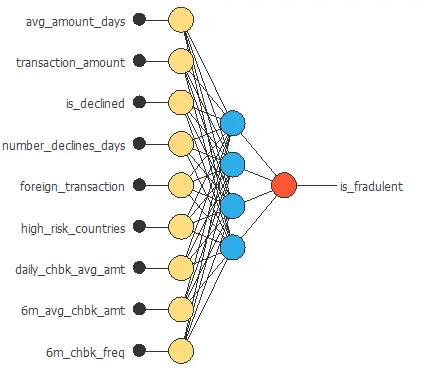
The graph above represents the architecture of the final neural network.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network. To validate a classification technique, we need to compare the values provided by this technique to the observed values.
ROC curve
We can use the ROC curve as it is the standard testing method for binary classification projects.
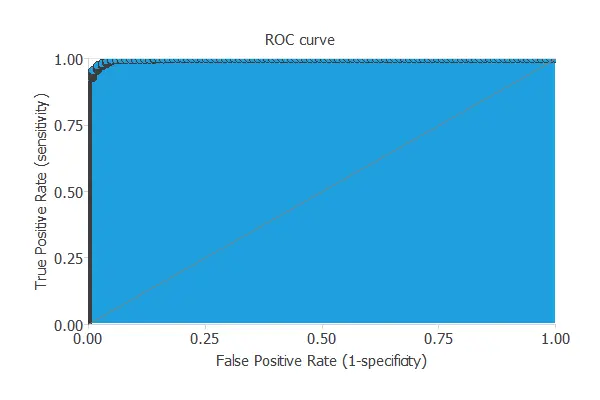
The AUC value for this example is 0.9982.
Confusion matrix
The following table contains the elements of the confusion matrix. This matrix contains the true positives, false positives, false negatives, and true negatives for the variable is_fraudulent.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 79 (12%) | 5 (0%) |
| Real negative | 8 (1%) | 523 (85%) |
The total number of testing samples is 615. Therefore, the number of correctly classified samples is 602 (97%), and the number of misclassified samples is 13 (2%).
Binary classification tests
The binary classification tests are parameters for measuring the performance of a classification problem with two classes:
- Classification accuracy (ratio of instances correctly classified): 97.9%
- Error rate (ratio of instances misclassified): 2.1%
- Sensitivity (ratio of real positives the model classifies as positives): 94%
- Specificity (ratio of real negatives the model classifies as negatives): 98.5%
We have correctly classified 94% of the fraudulent payments; we can identify around 19 out of 20 fraudulent charges.
We can also observe these results in the positive rates chart:
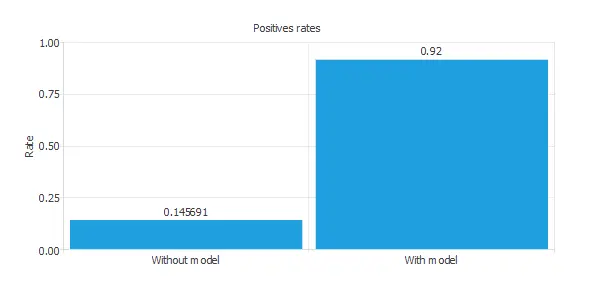
The initial positive rate was around 15%, and now, after applying our model, it is 92%. This means we could recognize six times more fraudulent payments with this model.
Cumulative gain
We can also perform the cumulative gain analysis, a visual aid showing the advantage of using a predictive model over randomness.
It consists of three lines. The baseline represents the results that would be obtained without using a model. The positive cumulative gain shows in the y-axis the percentage of positive instances found against the population represented in the x-axis.
Similarly, the negative cumulative gain shows the percentage of the negative instances found against the population percentage.
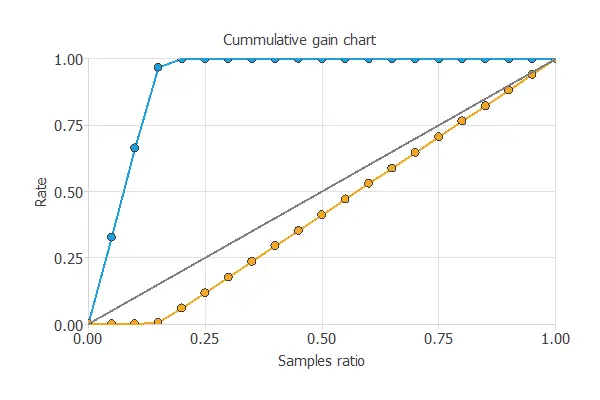
In this case, by using the model, we see that by analyzing 20% of the payments with a higher probability of being fraudulent, we would reach 100% of the fraudulent charges.
7. Model deployment
After all the steps, the model obtained is not the best to achieve. Nevertheless, it is still better than randomly guessing.
We can calculate the neural network outputs for a given set of inputs:
- avg_amount_day: 515.026.
- transaction_amount: 9876.4.
- is_declined: no.
- number_declines_day: 0.957398.
- foreign_transaction: yes.
- high_risk_country: yes.
- daily_chbk_avg_amt: 55.7376.
- 6m_avg_chbk_amt: 40.0224.
- 6m_chbk_freq: 0.39187.
The predicted output for these input values is the following:
- is_fradulent: 96% of been fraudulent.
The objective of the Response Optimization algorithm is to exploit the mathematical model to look for optimal operating conditions. Indeed, the predictive model allows us to simulate different operating scenarios and adjust the control variables to improve efficiency.
An example is to maximize the transaction amount while maintaining the fraudulent probability under the desired value.
The next table resumes the conditions for this problem.
| Variable name | Condition | |
|---|---|---|
| Avg amount days | None | |
| Transaction amount | Maximize | |
| Is declined | None | |
| Number declines days | None | |
| Foreign transaction | None | |
| High risk countries | None | |
| Daily chbk averge amount | None | |
| 6m average chbk amount | None | |
| 6m chbk frequencie | None | |
| Fraudulent probability | Less than | 0.5 |
The next list shows the optimum values for previous conditions.
- avg_amount_day: 1731.56.
- transaction_amount: 42128.2.
- is_declined: yes.
- number_declines_days: 0.183716.
- foreign_transaction: no.
- high_risk_country: yes.
- daily_chbk_avg_amt: 535.974.
- 6m_avg_chbk_amt: 363.012.
- 6m_chbk_freq: 3.5365.
- is_fraudulent: 32%.
The next listing shows the mathematical expression of the predictive model.
scaled_avg_amount_days = avg_amount_days*(1+1)/(2000-(4.01153))-4.01153*(1+1)/(2000-4.01153)-1; scaled_transaction_amount = transaction_amount*(1+1)/(108000-(0))-0*(1+1)/(108000-0)-1; scaled_is_declined = is_declined*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_number_declines_days = number_declines_days*(1+1)/(20-(0))-0*(1+1)/(20-0)-1; scaled_foreign_transaction = foreign_transaction*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_high_risk_countries = high_risk_countries*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_daily_chbk_avg_amt = daily_chbk_avg_amt*(1+1)/(998-(0))-0*(1+1)/(998-0)-1; scaled_6m_avg_chbk_amt = 6m_avg_chbk_amt*(1+1)/(998-(0))-0*(1+1)/(998-0)-1; scaled_6m_chbk_freq = 6m_chbk_freq*(1+1)/(9-(0))-0*(1+1)/(9-0)-1; perceptron_layer_0_output_0 = sigma[ -0.730652 + (scaled_avg_amount_days*0.347961)+ (scaled_transaction_amount*-0.866882)+ (scaled_is_declined*0.698547)+ (scaled_number_declines_days*-0.679199)+ (scaled_foreign_transaction*-0.744385)+ (scaled_high_risk_countries*-0.223877)+ (scaled_daily_chbk_avg_amt*-0.948853)+ (scaled_6m_avg_chbk_amt*0.281616)+ (scaled_6m_chbk_freq*-0.272766) ]; perceptron_layer_0_output_1 = sigma[ 0.757568 + (scaled_avg_amount_days*0.0680542)+ (scaled_transaction_amount*-0.254028)+ (scaled_is_declined*-0.58905)+ (scaled_number_declines_days*0.920654)+ (scaled_foreign_transaction*0.0759888)+ (scaled_high_risk_countries*0.961853)+ (scaled_daily_chbk_avg_amt*0.0324707)+ (scaled_6m_avg_chbk_amt*0.283447)+ (scaled_6m_chbk_freq*0.200012) ]; perceptron_layer_0_output_2 = sigma[ -0.406372 + (scaled_avg_amount_days*0.268921)+ (scaled_transaction_amount*0.124512)+ (scaled_is_declined*0.815247)+ (scaled_number_declines_days*-0.362366)+ (scaled_foreign_transaction*0.486023)+ (scaled_high_risk_countries*0.997009)+ (scaled_daily_chbk_avg_amt*0.286682)+ (scaled_6m_avg_chbk_amt*0.97644)+ (scaled_6m_chbk_freq*-0.848083) ]; perceptron_layer_0_output_3 = sigma[ 0.529846 + (scaled_avg_amount_days*-0.871521)+ (scaled_transaction_amount*0.977722)+ (scaled_is_declined*-0.771179)+ (scaled_number_declines_days*0.671753)+ (scaled_foreign_transaction*-0.0239868)+ (scaled_high_risk_countries*-0.501465)+ (scaled_daily_chbk_avg_amt*0.620178)+ (scaled_6m_avg_chbk_amt*-0.797546)+ (scaled_6m_chbk_freq*-0.429626) ]; probabilistic_layer_combinations_0 = -0.745667 -0.556274*perceptron_layer_0_output_0 -0.661987*perceptron_layer_0_output_1 +0.70813*perceptron_layer_0_output_2 -0.882507*perceptron_layer_0_output_3 is_fradulent = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);
This formula can also be exported to the software tool the company requires.
8. Video tutorial
You can watch the step-by-step tutorial video below to help you complete this Machine Learning example for free using the powerful machine learning software Neural Designer.
References
- The data for this problem has been taken from the Machine Learning Kaggle Repository.



