The objective of this example is to predict the default risk of a bank’s customers using machine learning.
This project’s primary outcome is reducing loan losses and achieving real-time scoring and limited monitoring.
This example focuses on a customer’s default payments at a bank. From the risk management perspective, the result of the predictive model of the probability of default will be more valuable than the binary classification of clients as credible or not credible.
The credit risk database used here concerns consumers’ default payments in Taiwan.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
This example is solved with Neural Designer. You can use the free trial to follow it step by step.
1. Application type
The variable we are predicting is binary (default or not). Therefore, this is a classification project.
The goal here is to model the probability of default as a function of the customer features.
2. Data set
The data set consists of four concepts:
- Data source.
- Variables.
- Instances.
- Missing values.
The data file credit_risk.csv contains the information used to create the model. It consists of 30,000 rows and 25 columns. The columns represent the variables, while the rows represent the instances.
Variables
This data set uses the following 23 variables:
- limit_balance: Amount of the given credit (NT dollar) includes both the individual consumer credit and their family (supplementary) credit.
- sex: Gender (1= male; 2= female).
- education_level: Education (1 = graduate school; 2 = university; 3 = high school; 4 = others).
- marital_status: Marital status (1 = married; 2 = single; 3 = others).
- age: Age (year).
- repayment_status_lag_1: Repayment status 1 month ago (-1 = pay duly; 1 = payment delay for one month; … ; 9 = payment delay for nine months and above).
- repayment_status_lag_2: Repayment status 2 months ago ( – 1 = pay duly; 1 = payment delay for one month; … ; 9 = payment delay for nine months and above).
- repayment_status_lag_3: Repayment status 3 months ago ( – 1 = pay duly; 1 = payment delay for one month; … ; 9 = payment delay for nine months and above).
- repayment_status_lag_4: Repayment status 4 months ago ( – 1 = pay duly; 1 = payment delay for one month; … ; 9 = payment delay for nine months and above).
- repayment_status_lag_5: Repayment status 5 months ago ( – 1 = pay duly; 1 = payment delay for one month; … ; 9 = payment delay for nine months and above).
- repayment_status_lag_6: Repayment status 6 months ago ( – 1 = pay duly; 1 = payment delay for one month; … ; 9 = payment delay for nine months and above).
- bill_state_amount_lag_1: Amount of bill statement 1 month ago (NT dollar).
- bill_state_amount_lag_2: Amount of bill statement 2 months ago (NT dollar).
- bill_state_amount_lag_3: Amount of bill statement 3 months ago (NT dollar).
- bill_state_amount_lag_4: Amount of bill statement 4 months ago (NT dollar).
- bill_state_amount_lag_5: Amount of bill statement 5 months ago (NT dollar).
- bill_state_amount_lag_6: Amount of bill statement 6 months ago (NT dollar).
- payment_amount_lag_1: Amount paid 1 month ago (NT dollar).
- payment_amount_lag_2: Amount paid 2 months ago (NT dollar).
- payment_amount_lag_3: Amount paid 3 months ago (NT dollar).
- payment_amount_lag_4: Amount paid 4 months ago (NT dollar).
- payment_amount_lag_5: Amount paid 5 months ago (NT dollar).
- payment_amount_lag_6: Amount paid 6 months ago (NT dollar).
- default: Failure to repay the loan.
Instances
Finally, the use of all instances is selected. Each patient has an instance that contains the input and target variables. Neural Designer divides the data into three subsets: training, validation, and testing, automatically assigning 60%, 20%, and 20% of the instances for training, generalization, and testing, respectively. More specifically, 18,000 samples are used here for training, 6,000 for selection, and 6,000 for testing.
Variables distribution
We can also calculate the data distributions for each variable. The following figure depicts the number of customers who repay the loan and those who do not.
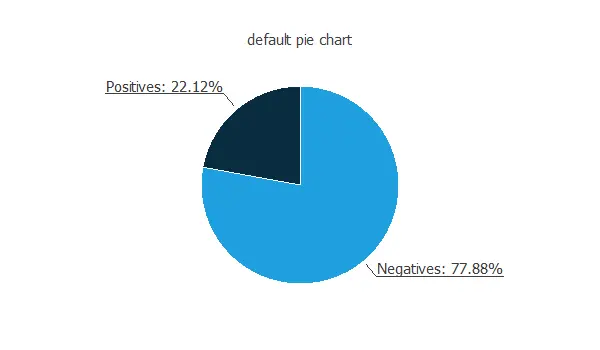
The data is unbalanced, as we can observe; this information will be used to configure the neural network later.
Inputs-targets correlations
The following figure depicts the inputs-targets correlations of all the inputs with the target. This helps us see the different inputs’ influence on the default.

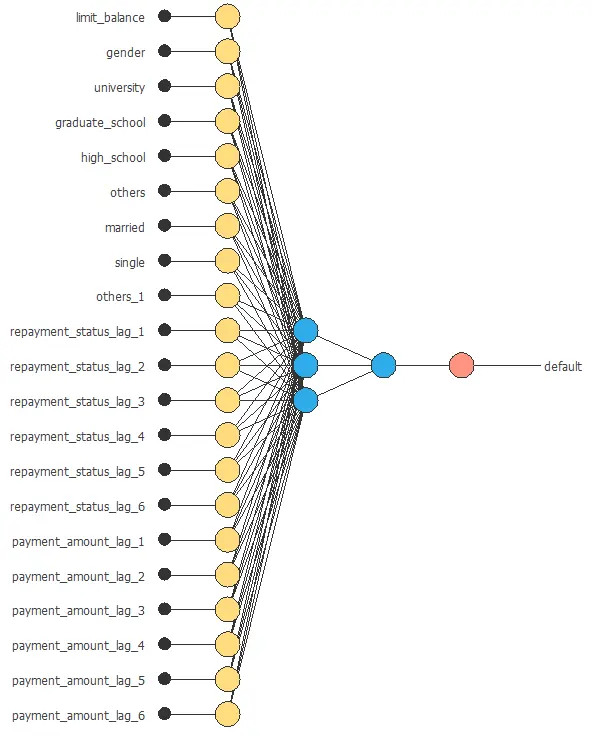
3. Neural network
The second step is to choose a neural network to represent the classification function. For classification problems, it is composed of:
- A scaling layer.
- Two perceptron layers.
- A probabilistic layer.
The mean and standard deviation scaling method is set for the scaling layer.
We set 2 perceptron layers, one hidden layer with 3 neurons as a first guess and one output layer with 1 neuron, both layers having the logistic activation function.
At last, we will set the continuous probabilistic method for the probabilistic layer.
The following figure shows the neural network used in this example.
4. Training strategy
The fourth step is to configure the training strategy, which is composed of two concepts:
- A loss index.
- An optimization algorithm.
The error term is the weighted squared error. It weights the squared error of negative and positive values. If the weighted squared error has a value of unity, then the neural network predicts the data ‘in the mean’, while a value of zero means a perfect prediction of the data.
In this case, the neural parameters norm weight term is 0.01. This parameter makes the model to be stable, avoiding oscillations.
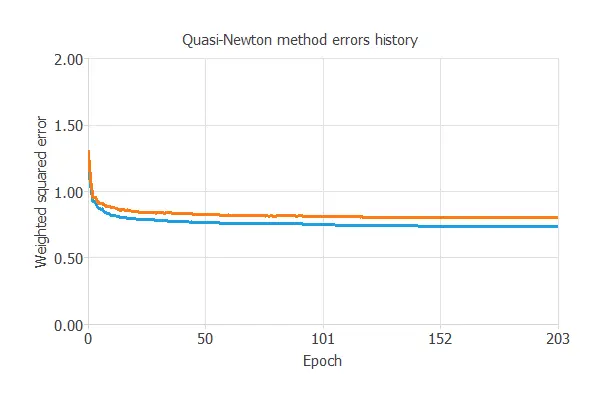
The optimization algorithm is applied to the neural network for the best performance. We choose the quasi-Newton method, and we leave the default parameters.
The following chart shows how training and selection errors decrease with the epochs during training.
The final results are training error = 0.755 WSE and selection error = 0.802 WSE, respectively.
5. Model selection
A model selection aims to find the network architecture with the best generalization properties, i.e., the one that minimizes the error on the selected instances of the data set.
More specifically, we want to find a neural network with a selection error of less than 0.802 WSE, the value we have achieved so far.
Order selection algorithms train several network architectures with different numbers of neurons and select the one with the smallest selection error.
The incremental order method starts with a few neurons and increases the complexity at each iteration.
The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.
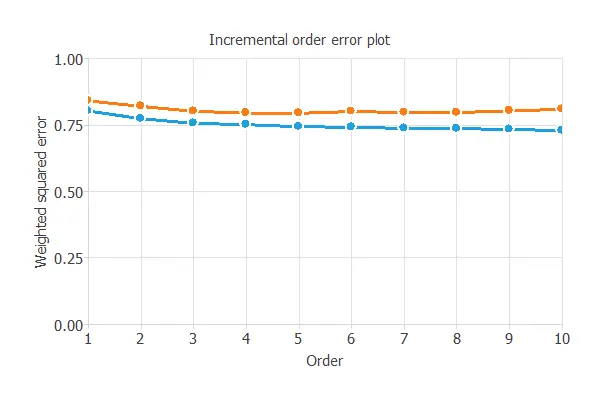
The final selection error achieved is 0.801 for an optimal number of neurons of 3.
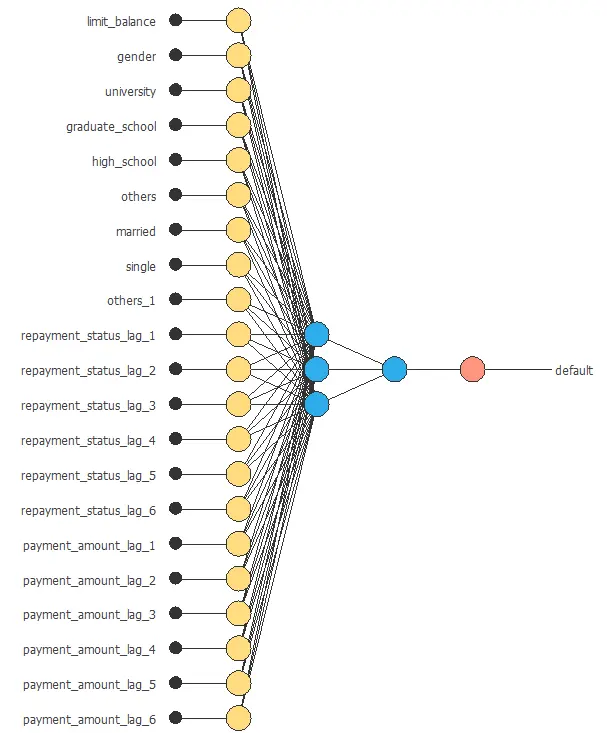
The graph above represents the architecture of the final neural network.
6. Testing analysis
The next step is to evaluate the trained neural network’s performance through exhaustive testing analysis. The standard way to do this is to compare the neural network’s outputs against previously unseen data, the training instances.
A common method to measure the generalization performance is the ROC curve. This is a graphical aid to study the classifier’s discrimination capacity. One of the parameters that can be obtained from this chart is the area under the curve (AUC). The closer to 1 area under the curve, the better the classifier. The following figure shows this measure for this example.
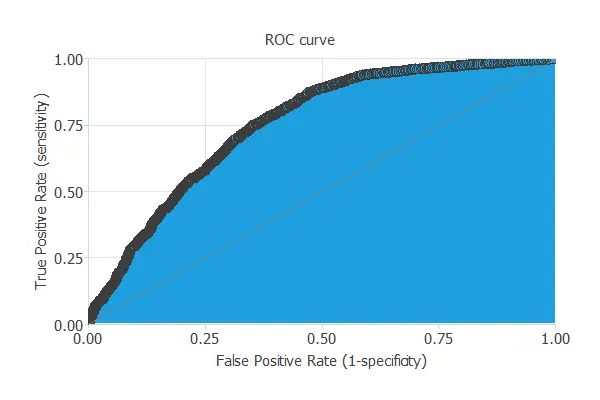
In this case, the AUC takes a high value: AUC = 0.772.
The following table contains the elements of the confusion matrix. This matrix contains the variable class’s true positives, false positives, false negatives, and true negatives.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 745 (12.4%) | 535 (8.92%) |
| Real negative | 893 (14.9%) | 3287 (63.8%) |
The binary classification tests are parameters for measuring the performance of a classification problem with two classes:
- Classification accuracy: 76.2% (ratio of correctly classified samples).
- Error rate: 23.8% (ratio of misclassified samples).
- Sensitivity: 58.2% (percentage of actual positive classified as positive).
- Specificity: 81.0% (percentage of actual negative classified as negative).
The classification accuracy is high (76.2%), meaning the prediction suits many cases.
We can also perform the cumulative gain analysis, a visual aid that shows the advantage of using a predictive model instead of randomness.
It consists of three lines. The baseline represents the results that would be obtained without using a model. The positive cumulative gain shows in the y-axis the percentage of positive instances found against the percentage of the population represented in the x-axis. Similarly, the negative cumulative gain shows the percentage of the negative instances found against the population percentage.
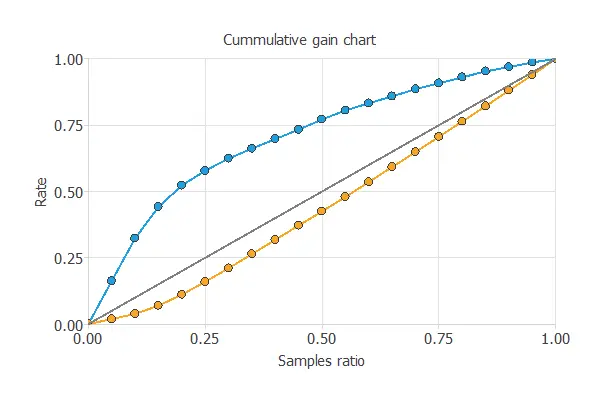
In this case, using the model, we see that analyzing 50% of the clients with a higher probability of default would reach more than 75% of clients with default payments.
7. Model deployment
Once the neural network’s generalization performance has been tested, it can be saved for future use in the so-called model deployment mode.
Below, the mathematical expression for the present model is displayed.
scaled_limit_balance = (limit_balance-167484)/129748;
scaled_gender = (gender-0.396267)/0.489129;
scaled_university = (university-0.473107)/0.499285;
scaled_graduate_school = (graduate_school-0.356938)/0.479104;
scaled_high_school = (high_school-0.165807)/0.371913;
scaled_others = (others-0.0041477)/0.06427;
scaled_married = (married-0.456121)/0.498079;
scaled_single = 2*(single-0)/(1-0)-1;
scaled_others_1 = (others_1-0.0107861)/0.103296;
scaled_repayment_status_lag_1 = (repayment_status_lag_1+0.0167)/1.1238;
scaled_repayment_status_lag_2 = (repayment_status_lag_2+0.133767)/1.19719;
scaled_repayment_status_lag_3 = (repayment_status_lag_3+0.1662)/1.19687;
scaled_repayment_status_lag_4 = (repayment_status_lag_4+0.220667)/1.16914;
scaled_repayment_status_lag_5 = (repayment_status_lag_5+0.2662)/1.13319;
scaled_repayment_status_lag_6 = (repayment_status_lag_6+0.2911)/1.14999;
scaled_payment_amount_lag_1 = (payment_amount_lag_1-5663.58)/16563.3;
scaled_payment_amount_lag_2 = (payment_amount_lag_2-5921.16)/23040.9;
scaled_payment_amount_lag_3 = (payment_amount_lag_3-5225.68)/17607;
scaled_payment_amount_lag_4 = (payment_amount_lag_4-4826.08)/15666.2;
scaled_payment_amount_lag_5 = (payment_amount_lag_5-4799.39)/15278.3;
scaled_payment_amount_lag_6 = (payment_amount_lag_6-5215.5)/17777.5;
y_1_1 = Logistic (2.17523+ (scaled_limit_balance*0.0536765)+ (scaled_gender*-0.152476)+ (scaled_university*-0.0121881)+ (scaled_graduate_school*-0.0306387)+ (scaled_high_school*0.173186)+ (scaled_others*-0.73854)+ (scaled_married*0.320037)+ (scaled_single*0.416477)+ (scaled_others_1*0.0952706)+ (scaled_repayment_status_lag_1*3.09033)+ (scaled_repayment_status_lag_2*0.680669)+ (scaled_repayment_status_lag_3*0.544463)+ (scaled_repayment_status_lag_4*0.287801)+ (scaled_repayment_status_lag_5*0.250001)+ (scaled_repayment_status_lag_6*0.642499)+ (scaled_payment_amount_lag_1*1.12996)+ (scaled_payment_amount_lag_2*0.314234)+ (scaled_payment_amount_lag_3*0.413271)+ (scaled_payment_amount_lag_4*0.0778191)+ (scaled_payment_amount_lag_5*0.219943)+ (scaled_payment_amount_lag_6*0.11853));
y_1_2 = Logistic (-0.497663+ (scaled_limit_balance*-0.335962)+ (scaled_gender*0.113687)+ (scaled_university*0.0570722)+ (scaled_graduate_school*-0.00269284)+ (scaled_high_school*0.00829173)+ (scaled_others*-0.36325)+ (scaled_married*-0.320526)+ (scaled_single*-0.409095)+ (scaled_others_1*-0.0420963)+ (scaled_repayment_status_lag_1*0.415076)+ (scaled_repayment_status_lag_2*0.706712)+ (scaled_repayment_status_lag_3*0.576033)+ (scaled_repayment_status_lag_4*-0.0251456)+ (scaled_repayment_status_lag_5*0.354822)+ (scaled_repayment_status_lag_6*0.0151421)+ (scaled_payment_amount_lag_1*0.0512893)+ (scaled_payment_amount_lag_2*0.000381215)+ (scaled_payment_amount_lag_3*0.13789)+ (scaled_payment_amount_lag_4*0.0193147)+ (scaled_payment_amount_lag_5*0.0986576)+ (scaled_payment_amount_lag_6*0.0923033));
y_1_3 = Logistic (1.98096+ (scaled_limit_balance*-0.268353)+ (scaled_gender*0.132924)+ (scaled_university*-0.158693)+ (scaled_graduate_school*-0.214737)+ (scaled_high_school*-0.273348)+ (scaled_others*0.559927)+ (scaled_married*0.0702353)+ (scaled_single*-0.0169948)+ (scaled_others_1*0.0913319)+ (scaled_repayment_status_lag_1*-1.64665)+ (scaled_repayment_status_lag_2*1.20179)+ (scaled_repayment_status_lag_3*0.865566)+ (scaled_repayment_status_lag_4*-0.733056)+ (scaled_repayment_status_lag_5*0.694502)+ (scaled_repayment_status_lag_6*-0.444317)+ (scaled_payment_amount_lag_1*0.402657)+ (scaled_payment_amount_lag_2*0.478144)+ (scaled_payment_amount_lag_3*0.998816)+ (scaled_payment_amount_lag_4*0.0466331)+ (scaled_payment_amount_lag_5*0.831399)+ (scaled_payment_amount_lag_6*0.261382));
non_probabilistic_default = Logistic (2.09934+ (y_1_1*-2.74891)+ (y_1_2*5.68963)+ (y_1_3*-3.45925));
default = probability(non_probabilistic_default);
logistic(x){
return 1/(1+exp(-x))
}
probability(x){
if x < 0 return 0 else if x > 1
return 1
else
return x
}
This expression can be exported elsewhere, such as to a bank’s software, to implement the prediction of these values.
References
- UCI Machine Learning Repository. Default of credit card clients data set.
- Yeh, I. C., & Lien, C. H. (2009). The comparisons of data mining techniques for the predictive accuracy of probability of default of credit card clients. Expert Systems with Applications, 36(2), 2473-2480.



