In this example, we will build a machine learning model to estimate car emissions, a topical issue that should raise awareness in the reader.
Nowadays, it is essential to reduce CO2 emissions in the atmosphere to fight against climate change. Indeed, many laws forbid cars whose CO2 emissions are above a specific limit; they must be below it to be approved to drive on the roads. We will predict CO2 emissions with certain independent variables.
Any car company could adjust this value by modifying parameters like the engine’s size and many other engine features. For this study, we have gathered an extensive data set of different types of cars that could exist anywhere in the world.
This example is solved with Neural Designer. To follow it step by step, you can use the free trial.
Contents
1. Application type
2. Data set
The first step is to prepare the data set, which is the source of information for the approximation problem. It is composed of:
- Data source.
- Variables.
- Instances.
Data source
The file co2_emissions.csv contains the data for this example. Here, the number of variables (columns) is 12, and the number of instances (rows) is 7385.
Variables
In that way, this problem has the following 12 variables:
Categorical variables
- make – Car brand.
- model – Specific car model.
- vehicle_class – Car body type.
- transmission – Transmission type: A (Automatic), AM (Automated manual), AS (Automatic with select shift), AV (Continuously variable), M (Manual).
- fuel_type – Fuel type: X (Regular gasoline), Z (Premium gasoline), D (Diesel), E (Ethanol/E85), N (Natural gas).
Numerical variables
- engine_size – Engine size (liters).
- cylinders – Number of cylinders.
- fuel_consumption_city – Fuel consumption in city driving (L/100 km).
- fuel_consumption_hwy – Fuel consumption on highways (L/100 km).
- fuel_consumption_comb (L/100 km) – Combined fuel consumption (55% city, 45% highway) in L/100 km.
- fuel_consumption_comb (mpg) – Combined fuel consumption in miles per gallon.
Target variable
- co2_emissions – Tailpipe CO₂ emissions for combined driving (g/km).
All the variables that appear in the study are inputs, except for ‘make’ and ‘model’, which have to stay “unused”, and ‘co2_emissions’, which is the output that we want to extract from this machine learning study.
Therefore, as one of the main goals of a Neural Network study is to minimize the Selection Error as much as possible, we can add ‘vehicle_class’ as an input.
As we can see, certain variables should stay “unused”, too. That is the case of ‘fuel_consumption’ (in city, highway, or combined). These instances could be targets of the study (CO2 and fuel consumption depend on each other), but it is more visual to see the CO2 emissions as the final output.
Instances
The data is randomly split into 60% training (4,431 samples), 20% selection (1,477 samples), and 20% testing (1,477 samples).
Variables distribution
Once all the data set information has been set, we will perform some analytics to check the quality of the data.
For instance, we can calculate the data distribution. The following figure depicts the histogram for the target variable.
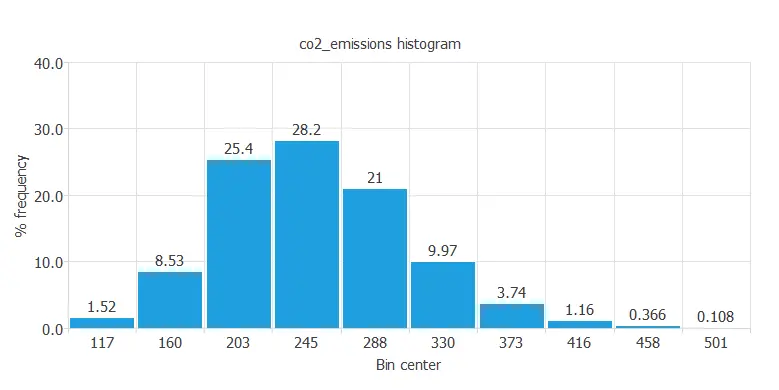
The chart shows that CO₂ emissions follow a normal distribution.
Most cars have median emissions below the discussed limit, while only 0.108% have very high emissions that are no longer allowed on the road.
Inputs-targets correlations
The following figure depicts input-target correlations. This might help us see the different inputs’ influence on the final car emissions.
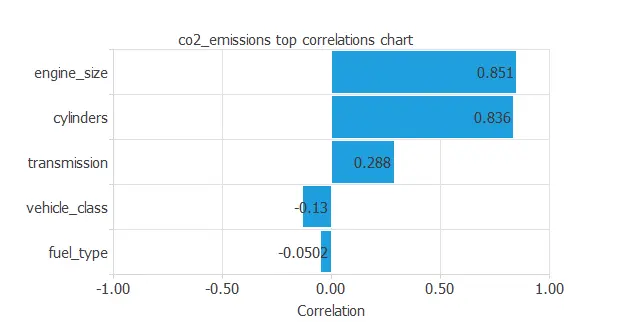
The chart shows that a few variables are highly related to CO₂ emissions.
For example, engine_size and cylinders correlate positively—larger engines emit more CO₂.
Scatter charts
We can also plot a scatter chart of CO2 emissions versus engine size.
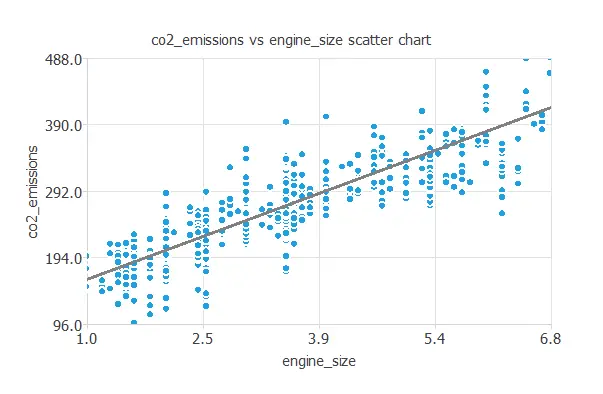
In general, the larger the engine size, the more emissions it produces. However, CO2 emissions depend on all the inputs simultaneously.
3. Neural network
The neural network will output the CO2 emissions as a function of consumption, transmission, and other car engine features.
In this approximation example, the neural network comprises:
- Scaling layer.
- Perceptron layers.
- Unscaling layer.
Scaling layer
The scaling layer transforms the original inputs to normalized values. Here, the mean and standard deviation scaling method is set so that the input values have a mean of 0 and a standard deviation of 1.
Perceptron layers
Here, two perceptron layers are added to the neural network. Subsequently, this number of layers is deemed sufficient for most applications. Specifically, the first layer comprises 28 inputs and 3 neurons, while the second layer consists of 3 inputs and 1 neuron.
Unscaling layer
The unscaling layer transforms the normalized values from the neural network into the original outputs. Here, the mean and standard deviation unscaling method will also be used.
Network architecture
The following figure shows the resulting network architecture.
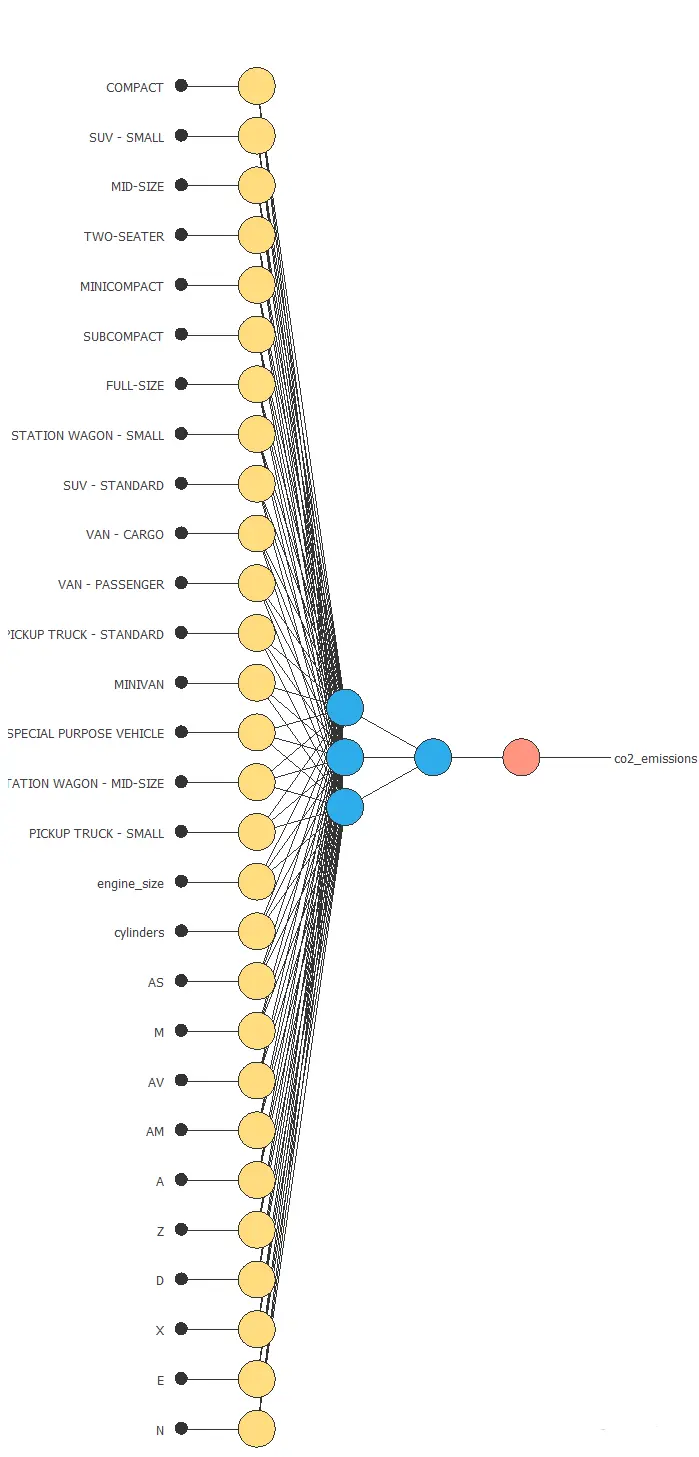
4. Training strategy
The next step is to select an appropriate training strategy that defines what the neural network will learn. A general training strategy is composed of two concepts:
- A loss index.
- An optimization algorithm.
Loss index
The loss index chosen is the normalized squared error with L2 regularization. This loss index is the default in approximation applications.
Optimization algorithm
The optimization algorithm chosen is the quasi-Newton method. This optimization algorithm is the default for medium-sized applications like this one.
Training process
Once we have set the strategy, we can train the neural network. The following chart shows how the training (blue) and selection (orange) errors decrease with the training epoch during the training process.
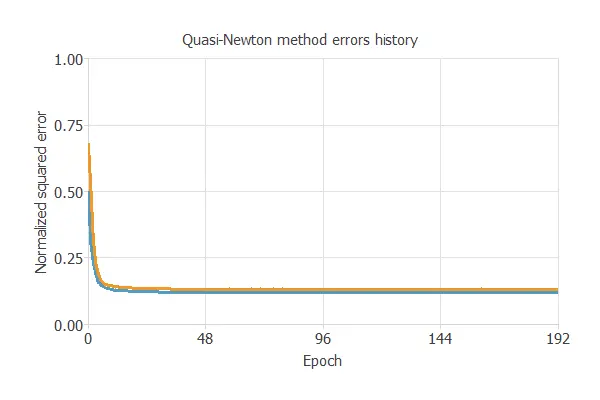
The most crucial training result is the final selection error. Indeed, this is a measure of the generalization capabilities of the neural network. Here, the final selection error is 0.145 NSE.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties. We want to improve the final selection error obtained before (0.145 NSE).
The best selection error is achieved using a model whose complexity is the most appropriate to produce an adequate data fit. Order selection algorithms are responsible for finding the optimal number of perceptrons in the neural network.
The final selection error takes a minimum value at some point. Here, the optimal number of neurons is 10, corresponding to a selection error of 0.131.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network. The testing compares the values provided by this technique to the observed values.
Goodness-of-fit
A standard testing technique in approximation problems involves performing a linear regression analysis between the predicted and the real values using an independent testing set. Consequently, the following figure illustrates a graphical output provided by this testing analysis.
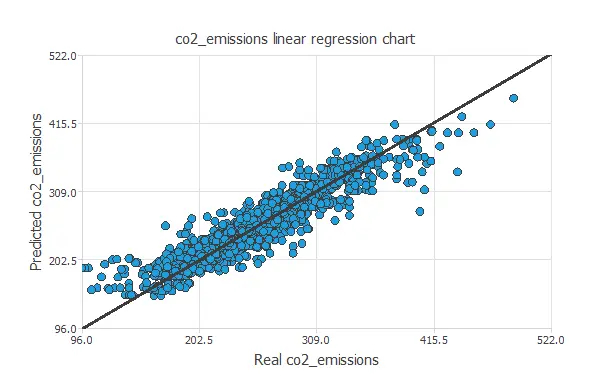
From the above chart, we can see that the neural network is predicting well the entire range of the CO2 emissions data.
The correlation value is R2 = 0.924, which is close to 1.
7. Model deployment
The model is now ready to estimate the CO2 emissions of a specific car with satisfactory quality over the same data range.
Directional output
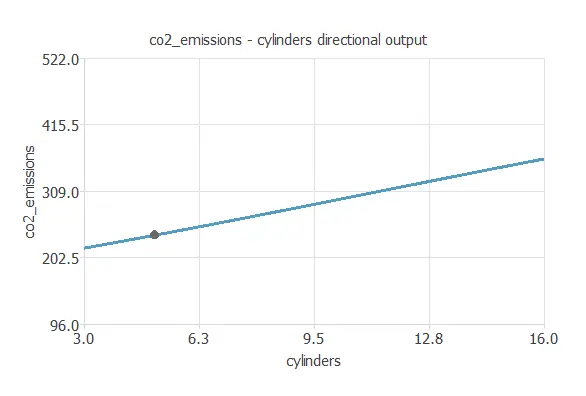
We can plot a directional output of the neural network to see how the emissions vary with a given input for all other fixed inputs. The following plot shows the CO2 emissions as a function of the number of cylinders through the following point:
- vehicle_class: COMPACT.
- engine_size: 3.16 L.
- cylinders: 5.
- transmission: AS.
- fuel_type: Z.
Mathematical expression
The co2-emissions.py contains the Python code for the CO2 emissions.
References
- Kaggle Machine Learning Repository. CO2 Emissions by Vehicles Data Set.



