An insurance company that already offers health insurance now wants to target customers likely to be interested in vehicle insurance.
To do this, we will build a machine learning model that predicts which customers are most likely to show interest.
Customer targeting involves identifying individuals who are more likely to be interested in a specific product or service.
This example is solved with Neural Designer. To follow this example step by step, you can use the free trial.
Contents
1. Application type
This project involves classification as the predictor variable is binary (interested or not interested).
The goal is to create a model to obtain the probability of interest as a function of customer features.
2. Data set
The data set contains information to create our model. We need to configure three things:
- Data source.
- Variables.
- Instances.
Data source
The data file used for this example is vehicle-insurances.csv, which contains 9 features about 381109 insurance company customers.
Variables
The data set includes the following variables:
Identification
ID: Unique identifier of the customer.
Customer Information
- Gender: Customer’s gender.
- Age: Customer’s age.
- Previously insured: Yes, if the customer already has vehicle insurance; no otherwise.
Vehicle Information
- Vehicle age: Age of the customer’s vehicle.
- Vehicle damage: Yes if the vehicle has been damaged in the past, no otherwise.
Financial Information
Annual premium: Yearly insurance premium to be paid by the customer.
Customer Relationship
Vintage: Number of days the customer has been associated with the company.
Target Variable
Response: Indicates whether the customer is interested in vehicle insurance (1 = yes, 0 = no).
Instances
On the other hand, the instances are divided randomly into training, selection, and testing subsets, containing 60%, 20%, and 20% of the instances, respectively.
Distributions
Our target variable is the response. We can calculate the data distributions and plot a pie chart with the percentage of instances for each class.
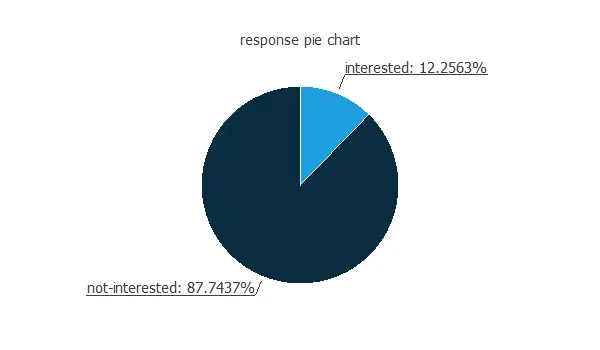
As we can see, the target variable is unbalanced, with almost 88% of customers showing no interest in vehicle insurance, while only 12% are interested.
Therefore, we could say that around 1 out of 10 customers is interested in vehicle insurance.
Input-target correlations
Furthermore, we can also compute the input-target correlations, which might indicate which factors significantly influence vehicle insurance.
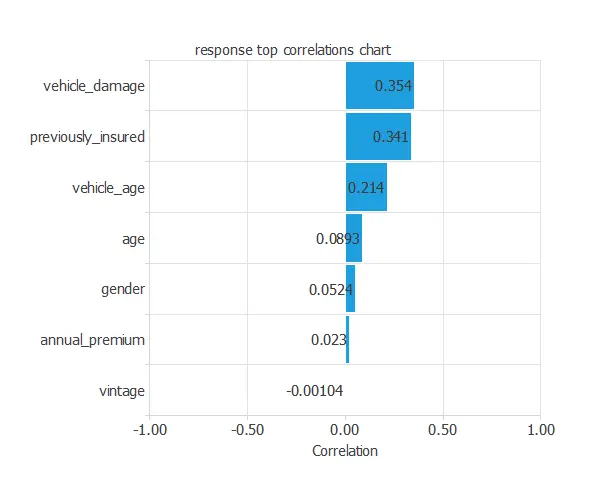
In this example, vehicle_damage and previously_insured are the two variables with the highest correlation; vehicle_damage has a positive correlation, while previously_insured has a negative correlation.
3. Neural network
The next step is to set the neural network parameters. Classification models usually contain the following layers:
- Scaling layer.
- Dense layers.
Scaling layer
For the scaling layer, we set the mean and standard deviation scaling method.
Dense layers
We set one perceptron layer with 3 neurons having the logistic activation function.
This layer has seven inputs, and since the target variable is binary, it has only one output.
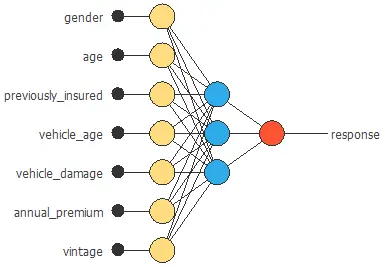
Neural network graph
The neural network for this example can be represented with the following diagram:
4. Training strategy
The fourth step is to set the training strategy, defining what the neural network will learn. A general training strategy for classification consists of two terms:
- A loss index.
- An optimization algorithm.
Loss index
The loss index chosen for this problem is the normalized squared error between the outputs from the neural network and the targets in the data set with L1 regularization.
Optimization algorithm
The selected optimization algorithm is the adaptive linear momentum.
The following chart shows how training and selection errors develop with the epochs during training.
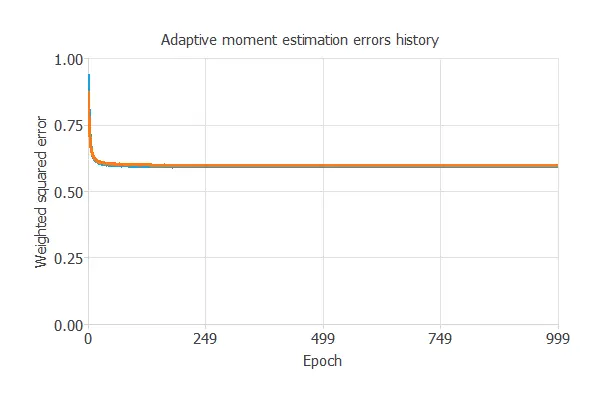
The final values are training error = 0.593 NSE and selection error = 0.598 NSE.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties, which means finding the one that minimizes the error on the selected instances of the data set.
More specifically, we aim to develop a neural network with a selection error of less than 0.598 NSE, the value we have previously achieved.
Order selection
Order selection algorithms train several network architectures with a different number of neurons and select the one with the smallest selection error.
The incremental order method starts with a few neurons and increases the complexity at each iteration.
The final selection error achieved is 0.587 for an optimal number of neurons of 6.
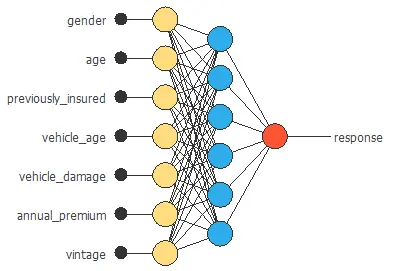
The graph above represents the architecture of the final neural network.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network.
ROC curve
To validate a classification technique, we need to compare the values provided by this technique to the observed values.
We can use the ROC curve as it is the standard testing method for binary classification projects.
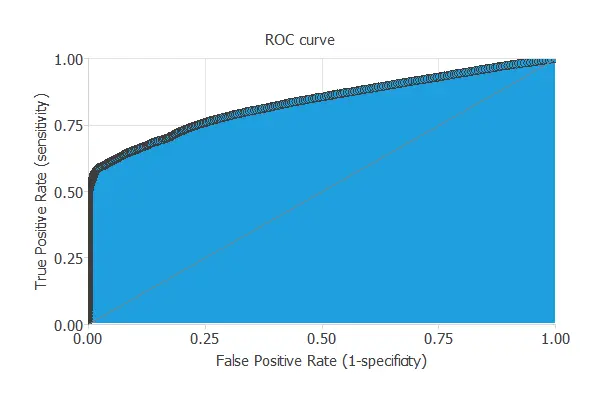
The AUC value for this example is 0.834.
Confusion matrix
The following table contains the elements of the confusion matrix. This matrix contains the true positives, false positives, false negatives, and true negatives for the variable response.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 9.1 ∙ 103 (11%) | 205 (0%) |
| Real negative | 2.75 ∙ 104 (36%) | 3.94 ∙ 104 (51%) |
The total number of testing samples is 76221. The number of correctly classified samples is 48519 (63%), and the number of misclassified samples is 27702 (36%).
Positives rates
We can also observe these results in the positive rates chart:
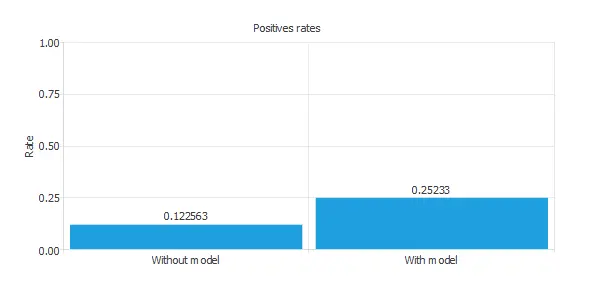
The initial positive rate was around 12%, and now, after applying our model, it is 25%. This means that we would be able to duplicate the vehicle insurance sales with this model.
Cumulative gain
We can also perform the cumulative gain analysis, a visual aid that shows the advantage of using a predictive model instead of randomness.
It consists of three lines. The baseline represents the results one would obtain without using a model. The positive cumulative gain shows in the y-axis the percentage of positive instances found against the population represented in the x-axis.
Similarly, the negative cumulative gain shows the percentage of the negative instances found against the population percentage.
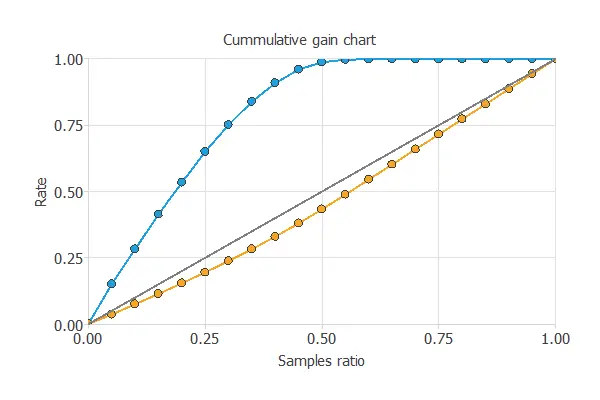
In this case, using the model reveals that analyzing 50% of clients with a higher probability of interest in vehicle insurance would result in almost 100% of clients taking out the insurance.
Profit chart
Another testing method is the profit chart.
This testing method shows the difference in profits from randomness and those using the model, depending on the instance ratio.
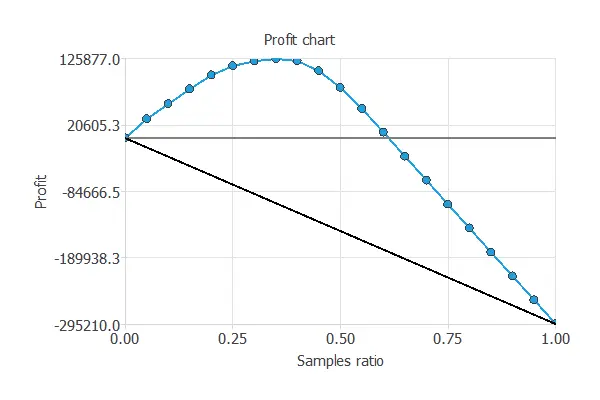
The values of the previous plot are displayed below:
- Unitary cost: 10 USD
- Unitary income: 50 USD
- Maximum profit: 125877 USD
- Samples ratio: 0.35
The graph shows that contacting 35% of the customers who are most likely interested in vehicle insurance, with a unitary cost of 10 USD and a unitary income of 50 USD, results in the maximum benefit of 125,877 USD.
7. Model deployment
Despite going through all the steps, the model we obtained is not the best it could have been. Nevertheless, it is still better than guessing randomly.
The objective of the Response Optimization algorithm is to exploit the mathematical model to look for optimal operating conditions. Indeed, the predictive model allows us to simulate different operating scenarios and adjust the control variables to improve efficiency.
An example is to maximize response probability while maintaining the age between two desired values.
The following table summarizes the conditions for this problem.
| Variable name | Condition | ||
|---|---|---|---|
| Gender | None | ||
| Age | Between | 30 | 50 |
| Previously insured | None | ||
| Vehicle age | None | ||
| Vehicle damage | None | ||
| Annual premium | None | ||
| Vintage | None | ||
| Response | Maximize |
The following list shows the optimum values for the previous conditions.
- gender: female.
- age: 44.
- previously_insured: 1 (yes).
- vehicle_age: 3.
- vehicle_damage: 1 (yes).
- annual_premium: 85848.8.
- vintage: 204.
- response: 80%.
8. Video tutorial
Watch the step-by-step tutorial video below to help you complete this Machine Learning example for free using the powerful machine learning software Neural Designer.
References
- We have obtained the data for this problem from the Machine Learning Repository Kaggle.


