This example builds a machine learning model to accurately detect forged banknotes.
For this purpose, we utilize a set of images taken from genuine and counterfeit banknote-like specimens.
Features such as wavelet variance, skewness, kurtosis, and image entropy are extracted from the images.
The final accuracy obtained by this method is 100% on an independent testing set.
This example is solved with Neural Designer. To follow it step by step, you can use the free trial.
Contents:
1. Application type
This is a classification project since the variable to be predicted is binary (fraudulent or legal).
The goal is to model the probability that a banknote is fraudulent as a function of its features.
2. Data set
Data source
The data file banknote_authentication.csv is the source of information for the classification problem.
The number of instances (rows) in the data set is 1372, and the number of variables (columns) is 5.
Variables
In that way, this problem has the following variables:
Image Features
- Variance of wavelet transformed image: Statistical variance of the wavelet-transformed image.
- Skewness of wavelet-transformed image: Measure of the asymmetry of the wavelet-transformed image distribution.
- Kurtosis of wavelet-transformed image: Measure of the “tailedness” (peakedness) of the wavelet-transformed image distribution.
- Entropy of image: Measure of the randomness or complexity of the image.
Target Variable
Counterfeit: Binary indicator of authenticity (0 = genuine banknote, 1 = counterfeit).
Instances
The instances are divided into training, selection, and testing subsets.
There are 824 instances for training (60%), 274 cases for selection (20%), and 274 cases for testing (20%).
Distributions
We can calculate the data distributions and plot a pie chart with the percentage of instances for each class.
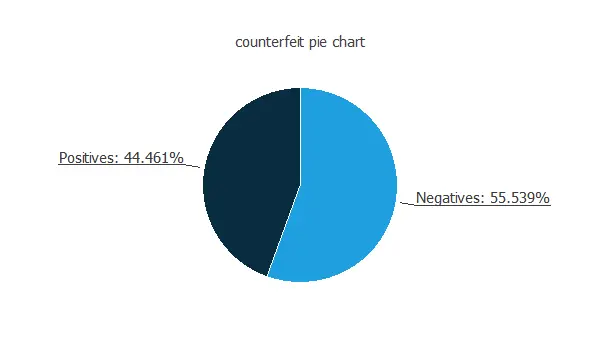
We can see that the numbers of authentic and forged banknotes are similar.
Input-target correlations
The input-target correlations might indicate which factors better discriminate between authentic and false banknotes.
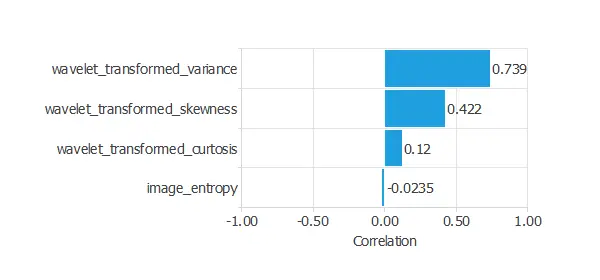
The above chart shows that the wavelet-transformed variance might be the most influential variable for this application.
3. Neural network
The second step is configuring a neural network to represent the classification function.
The following picture shows the neural network that defines the model.
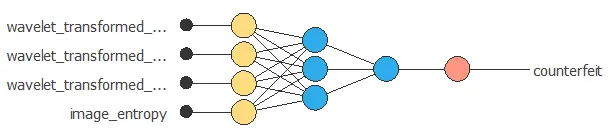
4. Training strategy
The fourth step is to set the training strategy, which is composed of:
- Loss index.
- Optimization algorithm.
We can state the learning problem as finding a neural network that minimizes the loss index.
Loss index
The loss index that we use is the weighted squared error with L2 regularization.
That is, we want a neural network that fits the data set (error term) and that does not oscillate (regularization term).
Optimization algorithm
We use here the quasi-Newton method as the optimization algorithm.
The default training parameters, stopping criteria, and training history settings are left.
Training
The following figure shows the loss history with the quasi-Newton method.
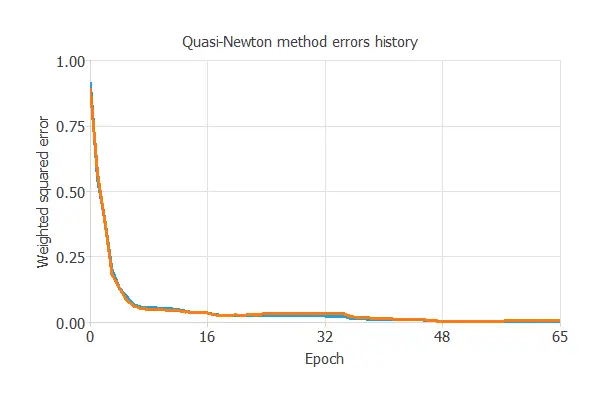
As we can see, the loss decreases until it reaches a stationary value. This is a sign of convergence.
The final training and selection errors are almost zero, which means the neural network fits the data well.
More specifically, the training error is 0.014 WSE, and the selection error is 0.011 WSE.
6. Testing analysis
The testing analysis aims to validate the generalization performance of the trained neural network.
ROC curve
A good measure for the precision of a binary classification model is the ROC curve.
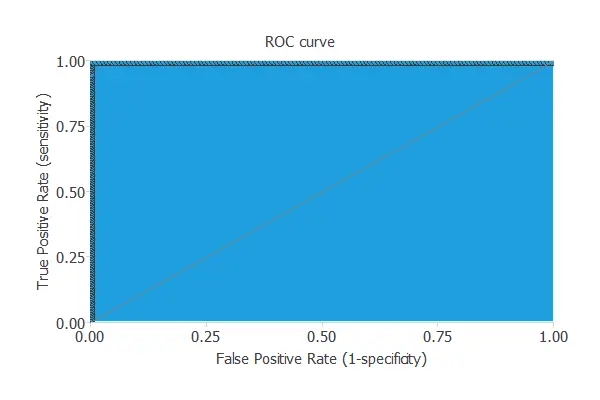
The area under the model’s curve is AUC = 1, indicating that the classifier accurately predicts all the testing instances.
Confusion matrix
In the confusion matrix, the rows represent the target classes, and the columns represent the predicted output classes for the testing target dataset.
The diagonal cells in each table show the number of correctly classified cases, and the off-diagonal cells show the misclassified instances.
The following table contains the elements of the confusion matrix.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 103 | 0 |
| Real negative | 0 | 171 |
The number of correctly classified instances is 274, and the number of misclassified cases is 0.
Since there are no misclassified patterns, the model accurately predicts the testing data.
7. Model deployment
In the model deployment phase, the neural network predicts outputs for inputs it has not seen before.
We can embed the neural network’s mathematical expression in the banknote authentication system. This expression is written below.
scaled_wavelet_transformed_variance = (wavelet_transformed_variance-0.433735)/2.84276;
scaled_wavelet_transformed_skewness = (wavelet_transformed_skewness-1.92235)/5.86905;
scaled_wavelet_transformed_curtosis = (wavelet_transformed_curtosis-1.39763)/4.31003;
scaled_image_entropy = (image_entropy+1.19166)/2.10101;
y_1_1 = Logistic (-2.95122+ (scaled_wavelet_transformed_variance*-3.20568)+ (scaled_wavelet_transformed_skewness*-4.57895)
+ (scaled_wavelet_transformed_curtosis*-5.83131)+ (scaled_image_entropy*0.125717));
y_1_2 = Logistic (3.23366+ (scaled_wavelet_transformed_variance*3.5863)+ (scaled_wavelet_transformed_skewness*2.36407)
+ (scaled_wavelet_transformed_curtosis*1.0865)+ (scaled_image_entropy*-1.0501));
non_probabilistic_counterfeit = Logistic (3.48838+ (y_1_1*9.72432)+ (y_1_2*-8.93277));
(counterfeit) = Probability(non_probabilistic_counterfeit);
Logistic(x){
return 1/(1+exp(-x))
}
Probability(x){
if x < 0
return 0
else if x > 1
return 1
else
return x
}
8. Conclusions
References
- Banknote authentication data set, UCI Machine Learning Repository.



