This example aims to build a machine learning model to assess bankruptcy risk from qualitative parameters from experts.
Risk assessment involves identifying hazards and risk factors that could potentially harm a business, including bankruptcy.
Bankruptcy is a legal proceeding involving a person or business unable to repay its outstanding debts.
Contents
This example is solved with Neural Designer. To follow this example step by step, you can use the free trial.
1. Application type
This is a classification project since the variable to predict is binary (bankruptcy or non-bankruptcy).
The goal is to model the probability of a business going bankrupt based on various features.
2. Data set
The data set contains information to create our model. We need to configure three things:
- Data source.
- Variables.
- Instances.
Data source
The data file used for this example is bankruptcy-prevention.csv, which contains 7 features about 250 companies.
Variables
The data set includes the following variables:
- industrial_risk: 0=low risk, 0.5=medium risk, 1=high risk.
- management_risk: 0=low risk, 0.5=medium risk, 1=high risk.
- financial_flexibility: 0=low flexibility, 0.5=medium flexibility, 1=high flexibility.
- credibility: 0=low credibility, 0.5=medium credibility, 1=high credibility.
- competitiveness: 0=low competitiveness, 0.5=medium competitiveness, 1=high competitiveness.
- operating_risk: 0=low risk, 0.5=medium risk, 1=high risk.
- class: bankruptcy, non-bankruptcy (target variable).
Instances
On the other hand, the instances are divided randomly into training, selection, and testing subsets, containing 60%, 20%, and 20% of the instances, respectively.
Distributions
Our target variable is class. We can calculate the data distributions and plot a pie chart with the percentage of instances for each class.
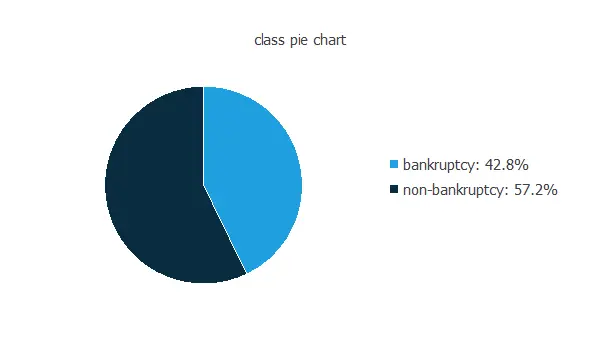
As we can see, the target variable is well-balanced. Indeed, 42.8% are positive samples and 57.8% are negative samples.
Input-target correlations
The correlations between inputs and targets might indicate which factors have the most significant influence on going into bankruptcy.
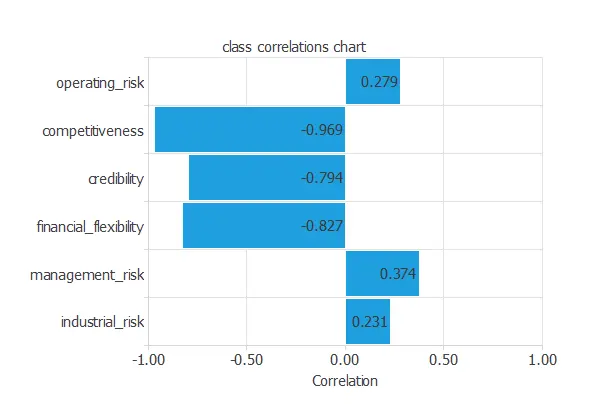
In this example, the variables that correlate the most with the target variable negatively correlate. Competitiveness is the variable with the highest correlation.
3. Neural network
The next step is to set the neural network parameters. For classification problems, it is composed of:
- Scaling layer.
- Dense layer.
Scaling layer
The mean and standard deviation scaling method has been set for the scaling layer.
Dense layer
We set up a single dense layer with one neuron, utilizing the logistic activation function. Since the target variable is binary, this layer has six inputs and only one output.
Neural network graph
The neural network for this example can be represented with the following diagram:
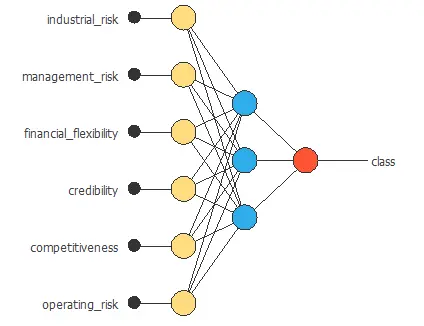
4. Training strategy
The fourth step is to set the training strategy, defining what the neural network will learn. A general training strategy for classification is composed of two terms:
- A loss index.
- An optimization algorithm.
Loss index
The loss index chosen for this problem is the normalized squared error between the outputs from the neural network and the targets in the data set with L1 regularization.
Optimization algorithm
The selected optimization algorithm is the Quasi-Newton method.
Training
The following chart shows how training and selection errors develop with the epochs during training.
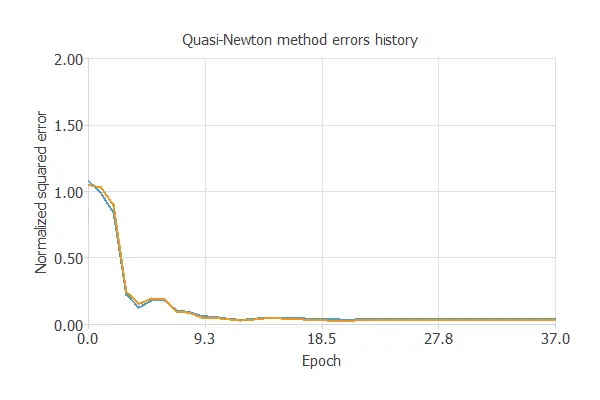
The final values are training error = 0.035 NSE and selection error = 0.028 NSE.
5. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network.
To validate a classification technique, we need to compare the values provided by this technique to the observed values.
ROC curve
We can use the ROC curve as it is the standard testing method for binary classification projects.
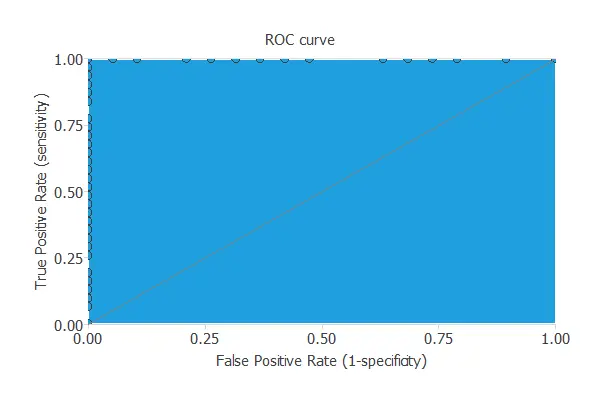
The AUC value for this example is 1.
Confusion matrix
The following table contains the elements of the confusion matrix.
This matrix contains the variable class’s true positives, false positives, false negatives, and true negatives.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 20 (40%) | 0 (0%) |
| Real negative | 0 (0%) | 30 (60%) |
The total number of testing samples is 50, all correctly classified.
Cumulative gain
We can also perform a cumulative gain analysis, a visual tool that compares a predictive model against random selection.
The chart includes three lines.
- The baseline represents what would be obtained by chance.
- The positive cumulative gain (y-axis) shows the percentage of positives found for each portion of the population (x-axis).
- The negative cumulative gain shows the percentage of negatives found in the same way.
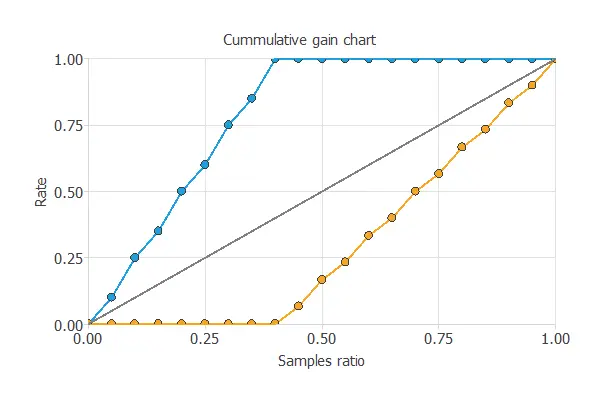
In this case, by focusing on the 40% of businesses with the highest predicted risk, the model identifies all companies that will go bankrupt.
7. Model deployment
In the model deployment phase, we use the neural network to predict the risk of a company.
References
- The data for this problem has been taken from the Machine Learning UCI Repository.



