This example shows how to develop a machine learning model for designing concrete mixtures with desired properties at a lower cost.
We use laboratory data from 425 specimens to develop a predictive model of compressive strength, the key property of concrete.
The analysis is carried out using the machine learning platform Neural Designer, which you can try with a free trial to follow the process step by step.
Contents
- Model type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
- Video tutorial.
1. Model type
Because compressive strength is continuous, we create an approximation model.
The primary goal here is to model the compressive strength as a function of the concrete components.
2. Data set
The first step is to prepare the data set, which is the source of information for the approximation problem. It is composed of:
- Data file.
- Variable information.
- Instance information.
Data file
The data file concrete_properties.csv contains 8 columns and 425 rows.
Variables
The following listing shows the variables in the data set and their use:
Input Variables (all in kg/m³)
- cement – Cement content.
- blast_furnace_slag – Blast furnace slag content.
- fly_ash – Fly ash content.
- water – Water content.
- superplasticizer – Superplasticizer content.
- coarse_aggregate – Coarse aggregate content.
- fine_aggregate – Fine aggregate content.
Target Variable
compressive_strength – Concrete compressive strength (MPa).
In summary, we have seven inputs and one target variable.
Instances
On the other hand, the instances are randomly split into training (60%), validation (20%), and testing (20%) subsets.
Distributions
Once we have set all the dataset information, we are ready to perform some analytics to check the data quality.
For instance, the following figure depicts the distribution for the target variable.
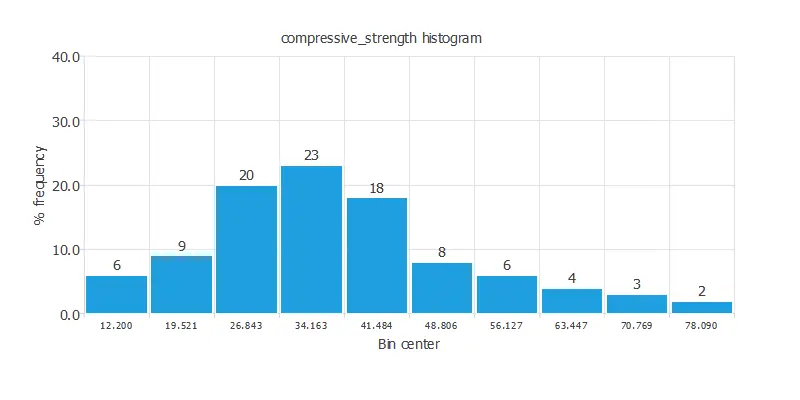
As we can see, the compressive strength has a normal distribution.
Input-target correlations
The following figure shows the input-target correlations, which illustrate the influence of each component on concrete compressive strength.
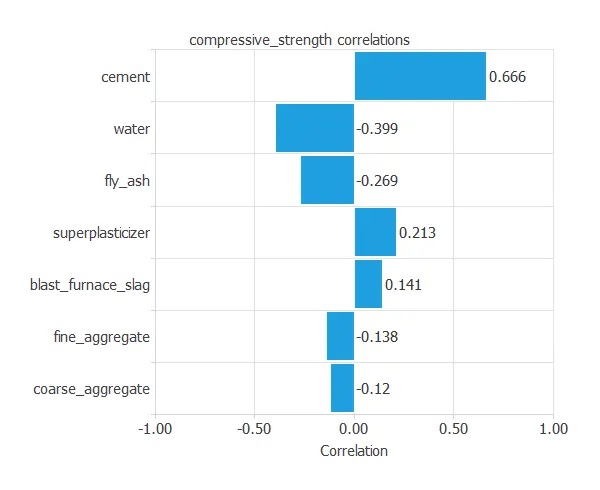
The above chart shows that cement has the most significant impact on compressive strength.
Scatter charts
We can also plot a scatter chart showing compressive strength versus the amount of cement.
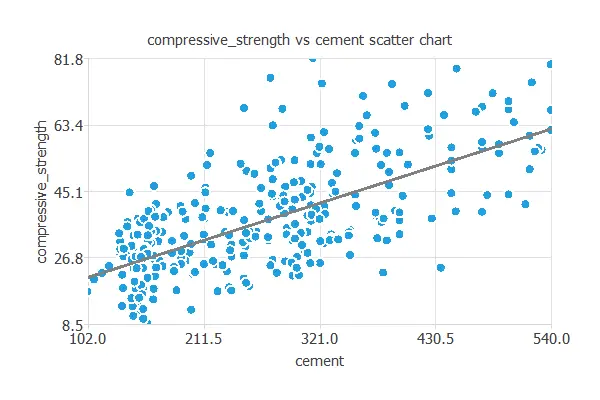
While cement content is a key factor, compressive strength results from the combined effect of all mixture variables.
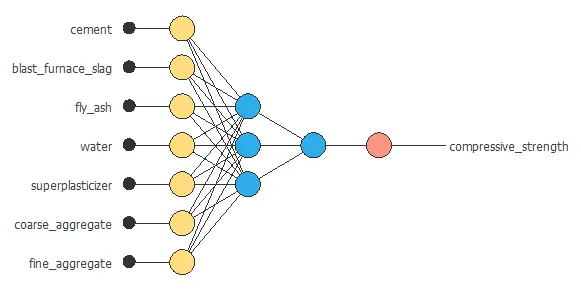
3. Neural network
The second step is to set up the neural network. For approximation project types, a neural network is usually composed of:
- Scaling layer.
- Dense layers.
- Unscaling layer.
Scaling layer
The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables.
Here, we set the minimum and maximum scaling method.
Nevertheless, the mean-standard deviation method would produce very similar results.
Dense layers
Here, two dense layers are added to the neural network.
This number of layers is enough for most applications.
The first layer has five inputs and three neurons.
The second layer has three inputs and one neuron.
The hyperbolic tangent and linear functions serve as the activation functions for the first and second layers, respectively.
These are the default values we will be using as a first guess.
Unscaling layer
The unscaling layer transforms the normalized values from the neural network into the original outputs.
Here, we also use the minimum and maximum unscaling method.
Neural network graph
4. Training strategy
The fourth step is to select an appropriate training strategy. It is composed of two parameters:
- A loss index.
- An optimization algorithm.
Loss index
As the loss index, we choose the normalized squared error with L2 regularization.
The normalized squared error divides the squared error between the outputs from the neural network and the targets in the data set by a normalization coefficient. If the normalized squared error is 1, then the neural network predicts the data ‘in the mean’, while zero means the perfect data prediction. This error term does not have any parameters to set.
We apply L2 regularization to control the neural network’s complexity by penalizing the values of its parameters. We apply here a weak regularization weight.
The learning problem can be stated as finding a neural network that minimizes the loss index. That is a neural network that fits the data set (error term) and does not oscillate (regularization term).
Optimization algorithm
The next step in solving this problem is to assign the optimization algorithm. We use the quasi-Newton method here.
Training
The neural network is trained to obtain the best possible performance.
The following chart shows the training history.
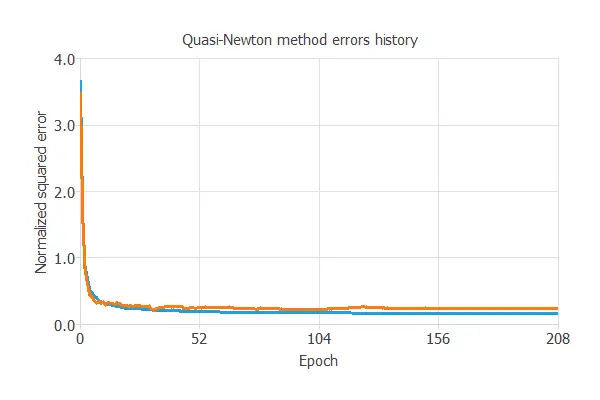
The final training and selection errors are a training error of 0.153 NSE and a selection error of 0.24 NSE, respectively.
The following section aims to improve generalization performance by reducing the selection error.
5. Model selection
The best generalization is achieved using a model with the most appropriate complexity to produce an adequate fit to the data.
Order selection is responsible for finding the optimal number of perceptrons. The algorithm selected for this purpose is the incremental order method.
The following image shows the result after the process. The blue line symbolizes the training error, and the orange represents the selection error.
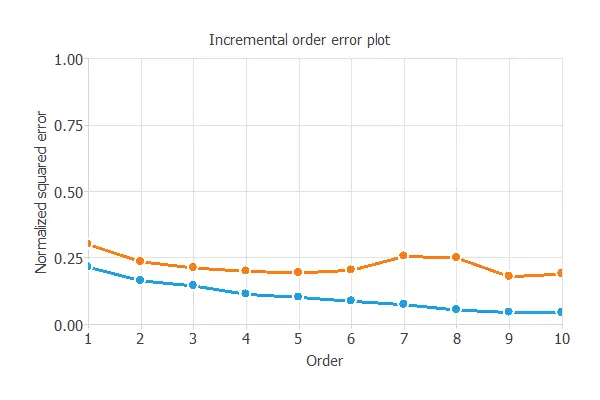
As shown in the picture, the method starts with a small number of neurons (order) and increases the complexity at each iteration.
The algorithm selects the order with the minimum selection loss. The selection error increases for greater values than this order due to overfitting, as it would result in a complex model.
After the order selection, we achieved a selection error of 0.211 NSE.
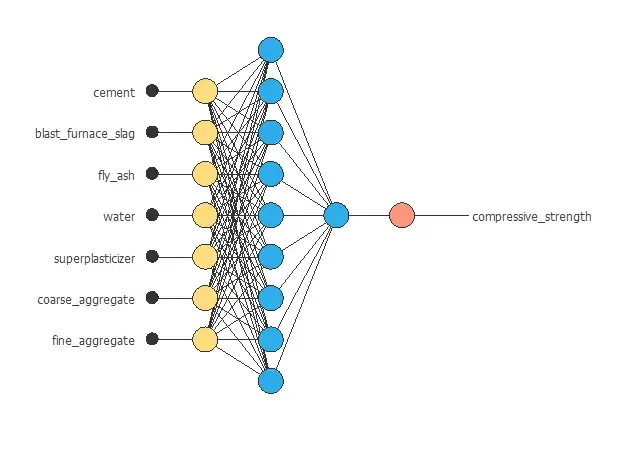
The figure above represents the final network architecture.
6. Testing analysis
A standard method for assessing the predictive performance of a regression model is to compare its outputs with an independent test dataset.
Goodnes-of-fit
The following plot shows the predicted compressive strength values versus the actual ones.
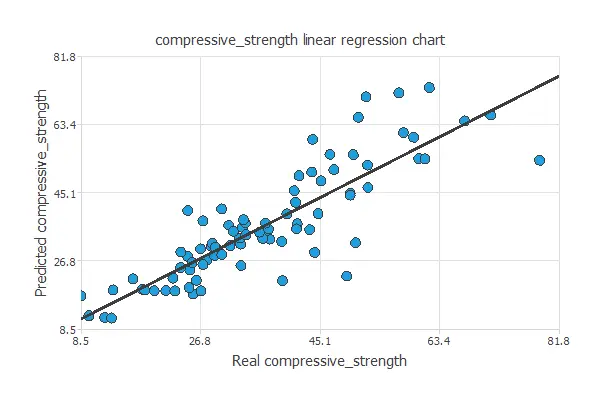
The predicted and observed values align closely, with a correlation coefficient of R² = 0.861, indicating strong predictive capability.
Finally, the mean error is 5.53%, with a standard deviation of 3.69%, indicating that the model achieves good accuracy.
7. Model deployment
After testing, the model can be deployed to design concretes with the desired properties.
Response optimization
Response optimization uses the predictive model to determine optimal operating conditions.
In this case, it can reduce cement content while maintaining the desired compressive strength.
The following table summarizes the conditions for this problem.
| Variable name | Condition | |
|---|---|---|
| Cement | Minimize | |
| Blast furnace slag | None | |
| Fly ash | None | |
| Water | None | |
| superplasticizer | None | |
| Coarse aggregate | None | |
| Fine aggregate | None | |
| Compressive strength | Greater than or equal to | 45 |
The next list shows the optimum values for the previous conditions.
- cement: 104 kg/m3.
- blast_furnace_slag: 192 kg/m3.
- fly_ash: 100 kg/m3.
- water: 217 kg/m3.
- superplasticizer: 18 kg/m3.
- coarse_aggregate: 1068 kg/m3.
- fine_aggregate: 939 kg/m3.
- compressive_strength: 52 MPa.
Conclusions
This example shows how machine learning can model and optimize concrete mixtures based on compressive strength.
By training a regression model with experimental data, it is possible to predict strength from mixture components with high accuracy.
Response optimization allows the design of concretes that meet desired properties while reducing material costs.
The analysis was performed using Neural Designer, a data science and machine learning tool for engineering applications.
References
8. Video tutorial
References
- I-Cheng Yeh, “Modeling of strength of high-performance concrete using artificial neural networks”, Cement and Concrete Research, Vol. 28, No. 12, pp. 1797-1808 (1998).