Introduction
Machine learning is enhancing dermatological diagnosis by improving accuracy in identifying erythemato-squamous diseases (ESDs), which often share overlapping clinical and microscopic features.
Accurate classification is key to effective treatment. We implemented a neural network using clinical and histopathological data from 366 patients, achieving 98.6% accuracy and demonstrating strong potential as a decision-support tool for distinguishing ESDs.
Healthcare professionals can test this methodology by downloading Neural Designer.
Contents
The following index outlines the steps for performing the analysis.
1. Model type
- Problem type: Multiclass classification (type of ESD: psoriasis, seborrheic dermatitis, etc.)
- Goal: Model the probability of each ESD type based on patient features and clinical variables to support diagnostic decision-making using artificial intelligence and machine learning.
2. Data set
Data source
The dermatology.csv dataset contains 366 instances and 35 variables for this example.
Variables
The following list summarizes the variables’ information:
Clinical features (0–3)
rythema – Skin redness.
scaling – Scaly skin.
definite_borders – Clear and sharp border separating the lesion from its surroundings.
itching – Unpleasant skin sensation that provokes scratching.
koebner phenomenon – New lesions appearing on areas of trauma in predisposed patients.
polygonal_papules – Shiny, flat-topped, firm elevations.
follicular_papules – Small, solid, circumscribed elevations (<1 cm).
oral_mucosal_involvement – Lesions inside the mouth.
knee and elbow involvement – Lesions on the knee and/or elbow.
scalp_involvement – Lesions on the scalp.
Demographic and family history
family_history (0 or 1) – Presence (1) or absence (0) of family history of dermatological disease.
age (years) – Age of the patient.
Histopathological features (0–3)
melanin_incontinence – Spillage of melanin into connective tissue.
eosinophils_infiltrate – Eosinophils infiltrating skin or mucosa.
pnl_infiltrate – Enlarged nerve trunks without skin lesions.
fibrosis_of_papillary_dermis – Excess fibrous tissue development.
exocytosis – Passage of foreign cells into the epidermis.
acanthosis – Thickened, darkened skin areas.
hyperkeratosis – Thickening of the outer skin layer.
parakeratosis – Retention of nuclei in the stratum corneum.
clubbing of rete ridges – Enlarged epithelial extensions into connective tissue.
elongation_of_rete_ridges – Lengthening of rete ridges.
thinning of suprapapillary epidermis – Thinning at papillary tips.
spongiform_pustule – Epidermal pustule with neutrophil infiltration.
munro_microabcess – Abscess in the stratum corneum due to neutrophil infiltration.
focal_hypergranulosis – Thickened granular layer.
disappearance of the granular layer – Loss of the skin granular layer.
vacuolisation and basal damage – Vacuolization and damage in basal skin cells.
spongiosis – Intercellular edema.
saw-tooth appearance of retes – Saw-tooth pattern of rete ridges.
follicular_horn_plug – Presence of follicular plugs.
perifollicular_parakeratosis – Retained nuclei around follicles.
inflammatory mononuclear infiltrate – Infiltration by mononuclear cells.
band_like_infiltrate – Banded infiltration pattern in basal epidermis.
Target variable
diagnose (categorical) – six possible classes (Psoriasis, Seborreic dermatitis, Lichen planus, Pityriasis rosea, Chronic dermatitis, and Pityriasis rubra pilaris)
Instances
The dataset’s instances are split into training (60%), validation (20%), and testing (20%) subsets by default.
You can adjust them as needed.
Variables distributions
We can calculate variable distributions; the figure shows a chart with the number of cases for each dermatological condition in the dataset.
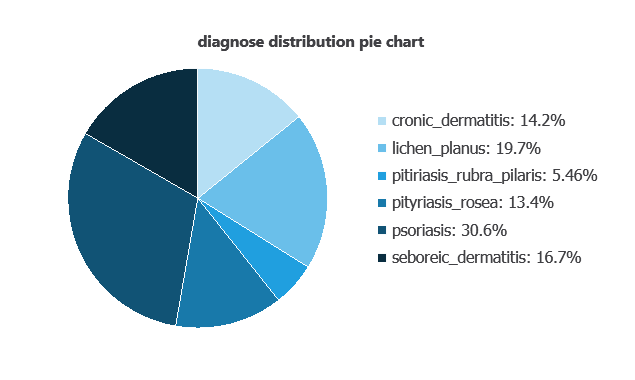
Psoriasis accounts for 30.6% of the samples, while pityriasis rubra pilaris represents the smallest proportion at 5.5%.
Input-target correlations
The input-target correlations indicate which clinical or diagnostic factors most influence each dermatological condition and, therefore, are more relevant to our analysis.
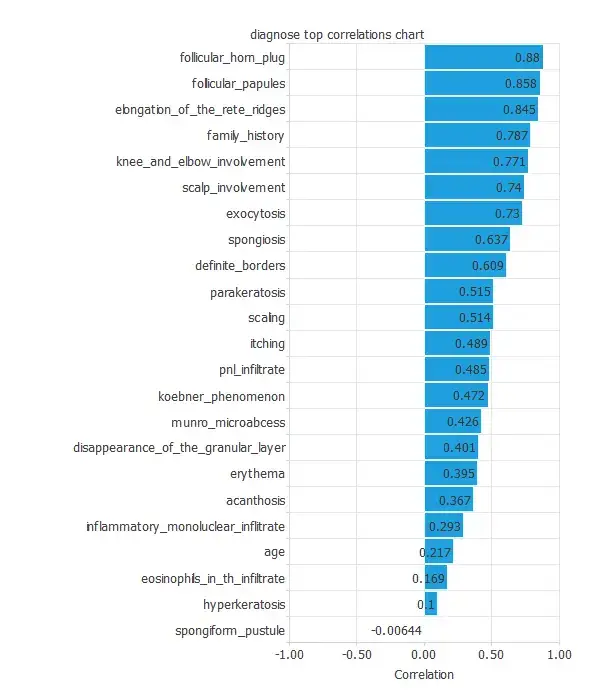
Here, the most correlated variables with malignant tumors are follicular horn plug, follicular papules, and elongation of the rete ridges.
3. Neural network
A neural network is an artificial intelligence model inspired by how the human brain processes information.
It is organized in layers: the input layer receives the variables, the hidden layers combine them to detect relevant patterns, and the output layer provides the probability of belonging to a given class.
Trained with historical data, the network learns to recognize patterns and distinguish between categories, offering objective support for decision-making.
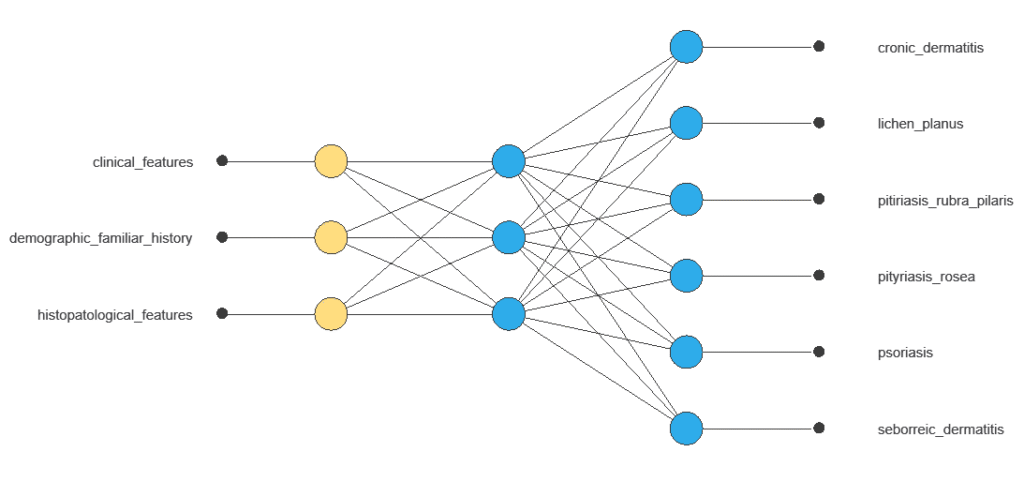
The network combines multiple inputs in a hidden layer to produce six outputs corresponding to different dermatological conditions, with connections showing each variable’s contribution.
4. Training strategy
Training a neural network uses a loss function to measure errors and an optimization algorithm to update the model, enabling it to learn from data while avoiding overfitting and performing well on new, unseen cases.
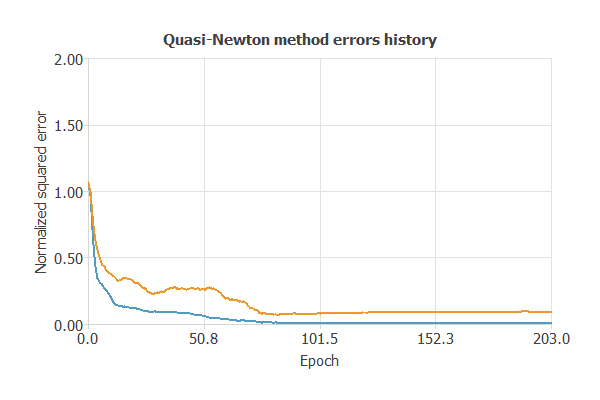
The model was trained for both accuracy and stability, with training and selection errors steadily decreasing (0.01 and 0.09 WSE), indicating effective learning and strong generalization to new instances.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties (that minimizes the error on the selected instances of the data set).
We aim to develop a neural network with a selection error of less than 0.09 WSE, which is the value we have achieved so far.
Model selection algorithms train several network architectures with a different number of neurons and select the one with the smallest selection error.
The neural selection method starts with a few neurons and increases the complexity at each iteration. The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.
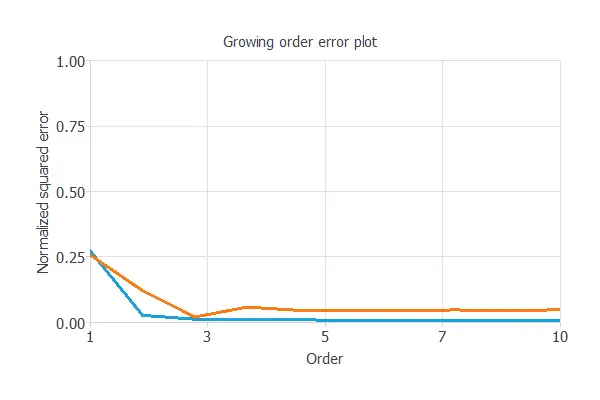
It shows that neuron selection does not significantly decrease the training error. But still, we obtained a minor error rate with four neurons.
input selection algorithms identify the subset of features that minimizes selection error and maximizes the network’s generalization capability.
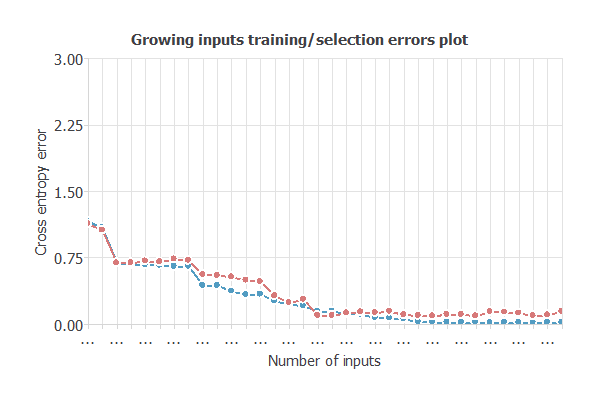
After selecting the optimal 30 inputs (4 unused), the model’s selection error dropped to 0.03 WSE, yielding a simpler, improved network with architecture 30:3:6 (inputs:hidden:outputs).
6. Testing analysis
Once we have trained the model, we perform a testing analysis to validate its prediction capacity.
We use a subset of previously unused data, specifically the testing instances.
Confusion matrix
The confusion matrix shows the model’s performance by comparing predicted and actual diagnoses. It includes:
True positives: cases correctly identified as having the condition
False positives: cases incorrectly identified as having the condition
False negatives: cases with the condition incorrectly identified as not having it
True negatives: cases correctly identified as not having the condition
| Predicted seboreic dermatitis | Predicted soriasis | Predicted lichen planus | Predicted chronic dermatitis | Predicted pityriasis rosea | Predicted rubra pilaris | |
|---|---|---|---|---|---|---|
| Real seboreic dermatitis | 10 | 0 | 0 | 0 | 0 | 0 |
| Real soriasis | 0 | 24 | 0 | 0 | 0 | 0 |
| Real lichen planus | 0 | 0 | 15 | 0 | 0 | 0 |
| Real chronic dermatitis | 0 | 0 | 0 | 11 | 0 | 0 |
| Real pityriasis rosea | 0 | 0 | 0 | 0 | 9 | 0 |
| Real pitiriasis rubra pilaris | 0 | 0 | 0 | 0 | 0 | 3 |
In this example, 98.63% of cases were correctly classified and 1.37% of cases were misclassified.
7. Model deployment
Once validated, the neural network can be saved for deployment, allowing predictions of dermatological conditions for new patients using clinical, histopathological, demographic, and lesion data.
It serves as a reliable diagnostic support tool, complements traditional examinations, and integrates easily via Neural Designer, though the network cannot be practically visualized due to many input variables.
Conclusions
The dermatology machine learning model achieved 98.6% accuracy in classifying erythemato-squamous diseases.
Key features—like follicular horn plugs, follicular papules, and rete ridge elongation—align with established dermatological criteria.
Its strong generalization allows it to support clinicians in differentiating conditions quickly and reliably, complementing traditional examinations and improving patient care.
References
- We have obtained the data for this problem from the UCI Machine Learning Repository.
- Nilsel Ilter, M.D., Ph.D., Gazi University, School of Medicine.
- H. Altay Guvenir, PhD., Bilkent University, Department of Computer Engineering and Information Science.