The goal is to model the patient’s status (dead or alive). This approach is based on clinical data, including variables extracted from blood tests using artificial intelligence and machine learning.

2. Data set

The heart_failure.csv file contains the data for this example. Target variables can only have two values in a classification model: 0 (false, alive) or 1 (true, deceased), depending on the event’s occurrence. The number of patients (rows) in the data set is 299, and the number of variables (columns) is 12.

Variables

The number of input variables, or attributes for each sample, is 11. The target variable is 1, death_event (1 or 0), whether or not the patient has died or survived. The following list summarizes the variables information:

• age: Age of the patient
• anaemia: Low red blood cells or hemoglobin count.
• creatinine_phosphokinase: Level of the CPK enzyme in the blood.
• diabetes: If the patient has diabetes.
• ejection_fraction: Percentage of blood leaving.
• high_blood_pressure: If a patient has hypertension.
• platelets: Platelets in the blood.
• serum_creatinine: Level of creatinine in the blood.
• serum_sodium: Level of sodium in the blood.
• sex: Woman or man.
• smoking: If the patient smokes.
• death_event: If the patient died during the follow-up period.

Instances

To start, we use all instances. Each instance contains the input and target variables of a different patient. The data set is divided into training, validation, and testing subsets. Neural Designer automatically assigns 60% of the instances for training, 20% for selection, and 20% for testing. The user can choose to modify these values to the desired ones.

Variables distributions

Also, we can calculate the distributions for all variables. The following figure is a pie chart showing which patients are dead (1) or alive (0) in the data set.

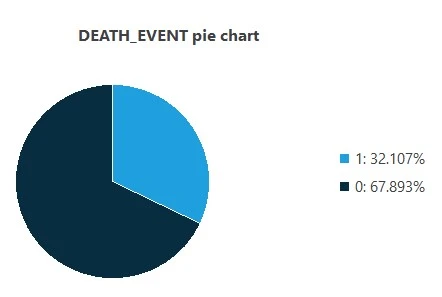
The image shows that dead patients represent 32.107% of the samples, while live patients represent 67.893%.

Inputs-targets correlations

The inputs-targets correlations might indicate which factors have the most univariate influence on whether or not a patient will live.

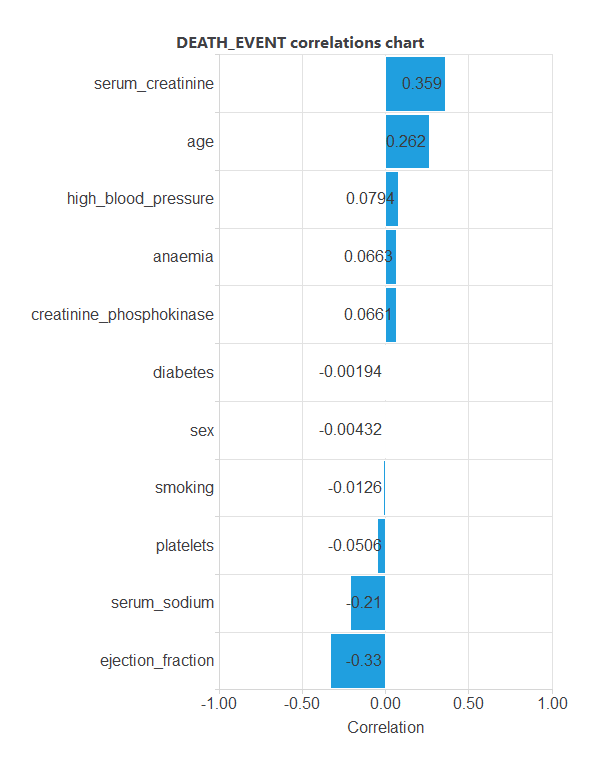
Here, the most correlated variables with survival status are serum_creatinine, age, serum_sodium, and ejection_fraction.

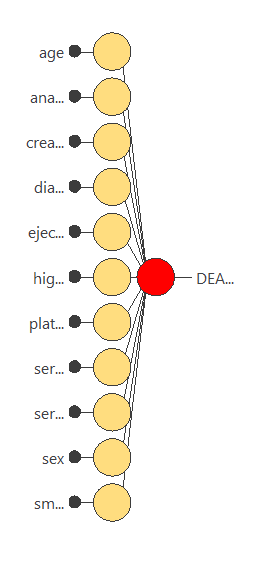
3. Neural network

The next step is to set up a neural network representing the classification function. For this class of applications, the neural network is composed of:

• Scaling layer.
• Perceptron layer.
• Probabilistic layer.

The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables. Here, the minimum-maximum method has been set. As we use 11 input variables, the scaling layer has 11 inputs.

We won’t use a perceptron layer to stabilize and simplify our model.

The probabilistic layer only contains the method for interpreting the outputs as probabilities. Moreover, as the output layer’s activation function is logistic, that output can already be interpreted as a probability of class membership.
The probabilistic layer has 11 inputs. It has one output, representing the probability of a patient being dead or alive.

The following figure is a graphical representation of this neural network.

4. Training strategy

The fourth step is to set the training strategy, which is composed of two terms:

• A loss index.
• An optimization algorithm.

The loss index is the weighted squared error with L2 regularization, the default loss index for binary classification applications.

We can state the learning problem as finding a neural network that minimizes the loss index. That is a neural network that fits the data set (error term) and does not oscillate (regularization term).

The optimization algorithm that we use is the quasi-Newton method, which is also the standard optimization algorithm for this type of problem.

The following chart shows how errors decrease with the iterations during training. The final training and selection errors are training error = 0.632681 WSE and selection error = 0.899055 WSE, respectively.

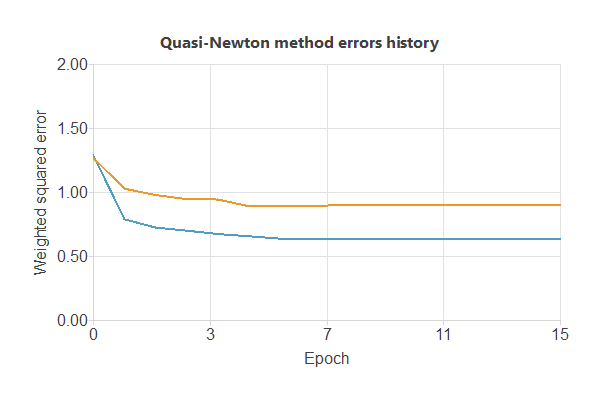
As we can see in the previous image, the curves have converged. However, the selection error is greater than the training error, so we could try to continue improving the model to reduce the errors further.

5. Model selection

The objective of model selection is to find the network architecture that minimizes the error, that is, with the best generalization properties for the selected instances of the data set.

Order selection algorithms train several network architectures with different numbers of neurons and select that with the smallest selection error. We have removed our perceptron layer to stabilize our model, so we cannot use this feature.

However, we will use input selection to select features in the data set that provide the best generalization capabilities.

The following image shows the training and selection errors as a function of the number of inputsusing this method.

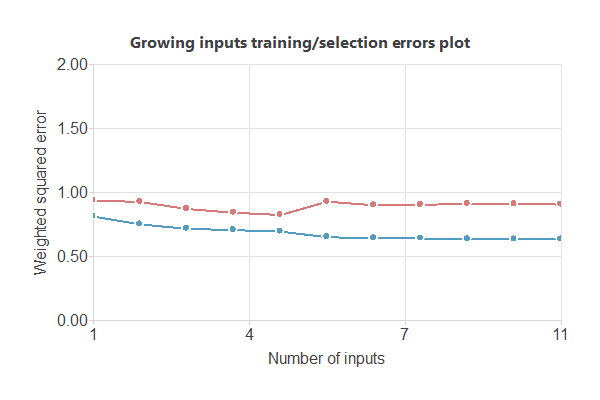
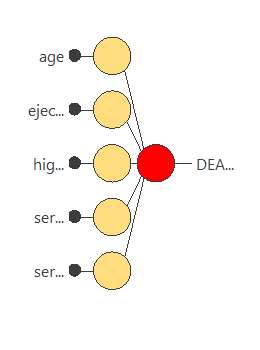
In the end, we obtain a training error = 0.6934 WSE and a selection error = 0.8234 WSE, respectively. Also, we have reduced the number of inputs to only 5 features. Our network is now like this:

6. Testing analysis

The objective of testing analysis is to validate the performance of the generalization properties of the trained neural network. To validate a classification technique, we need to compare the values provided by this technique to the observed values. We can use the ROC curve as it is the standard testing method for binary classification projects.

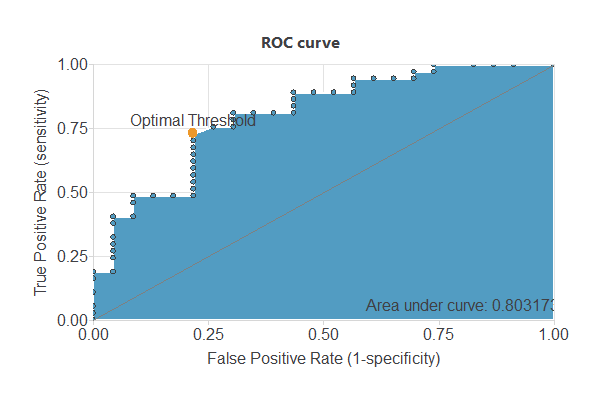
A random classifier has an area under a curve of 0.5, while a perfect classifier has a value of 1. The closer this value is to 1, the better the classifier. In this example, this parameter is AUC = 0.80317, which means a good performance.

The following table contains the elements of the confusion matrix. This matrix contains the true positives, false positives, false negatives, and true negatives for the variable diagnosis.

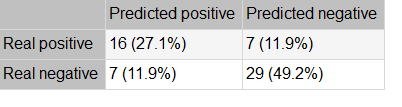
The binary classification tests are parameters for measuring the performance of a classification problem with two classes:

• Classification accuracy (ratio of instances correctly classified): 0.762
• Error rate (ratio of instances misclassified): 0.237
• Specificity (ratio of real positives that the model predicts as positives): 0.805
• Sensitivity (ratio of real negatives that the model predicts as negatives): 0.695

7. Model deployment

Once we have tested the neural network’s generalization performance, we can save it for future use in the so-called model deployment mode.

The mathematical expression represented by the neural network is written below.

scaled_age = (age-60.83390045)/11.89480019;
scaled_ejection_fraction = (ejection_fraction-38.08359909)/11.83479977;
scaled_high_blood_pressure = high_blood_pressure*(1+1)/(1-(0))-0*(1+1)/(1-0)-1;
scaled_serum_creatinine = (serum_creatinine-1.39388001)/1.034510016;
scaled_serum_sodium = (serum_sodium-136.625)/4.412479877;

probabilistic_layer_combinations_0 = -0.0438098 +0.506346*scaled_age -0.862699*scaled_ejection_fraction +0.321015*scaled_high_blood_pressure +1.73723*scaled_serum_creatinine -0.35006*scaled_serum_sodium 
					
DEATH_EVENT = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);

References

• The data for this problem has been collected by the Institutional Review Board of Government College University, Faisalabad-Pakistan, available at Plos One Repository.

Related posts