This example aims to catalog different chemical biodegradability using machine learning. QSAR (Quantitative Structure-Activity Relationships) models are currently being developed more frequently.
To construct the QSAR model, we leverage the explainable machine learning platform Neural Designer. For those interested in a hands-on experience, a free trial lets you meticulously follow the process.
Contents
1. Application type
The variable to be predicted can have two values (ready or not ready biodegradable molecule).
Thus, this is a binary classification project. The goal here is to observe the correlation between different molecular descriptors and the biodegradability of a molecule.
2. Data set
Data source
The file biodegradation.csv contains 1055 samples of chemicals, each with 41 inputs, and one is a binary target.
Variables
This data set contains the following variables:
- SpMax_L: Leading eingvalue from Laplace matrix.
- J_Dz(e): Balaban-like index from Barysz matrix weighted by Sanderson electronegativity.
- nHM: Number of heavy atoms.
- F01[N-N]: Frequency of N-N at topological distance 1.
- F04[C-N]: Frequency of C-N at topological distance 4.
- NssssC: Number of atoms of type ssssC.
- nCb: Number of substituted benzene C(sp2).
- C%: Percentage of C atoms.
- nCp: Number of terminal primary C(sp3).
- nO: Number of oxygen atoms.
- F03[C-N]: Frequency of C-N at topological distance 3.
- SdssC: Sum of dssC E-states.
- HyWi_B(m): Hyper-Wiener-like index (log function) from Burden matrix weighted by mass.
- LOC: Lopping centric index.
- SM6_L: Spectral moment of order 6 from Laplace matrix.
- F03[C-O]: Frequency of C – O at topological distance 3.
- Me: Mean atomic Sanderson electronegativity (scaled on Carbon atom).
- Mi: Mean first ionization potential (scaled on Carbon atom).
- nN-N: Number of N hydrazines.
- nArNO2: Number of nitro groups (aromatic).
- nCRX3: Number of CRX3.
- SpPosA_B(p): Normalized spectral positive sum from Burden matrix weighted by polarizability.
- nCIR: Number of circuits.
- B01[C-Br]: Presence/absence of C – Br at topological distance 1.
- B03[C-Cl]: Presence/absence of C – Cl at topological distance 3.
- N-073: Ar2NH / Ar3N / Ar2N-Al / R..N..R
- SpMax_A: Leading eigenvalue from adjacency matrix (Lovasz-Pelikan index).
- Psi_i_1d: Intrinsic state pseudoconnectivity index – type 1d.
- B04[C-Br]: Presence/absence of C – Br at topological distance 4.
- SdO: Sum of dO E-states.
- TI2_L: Second Mohar index from Laplace matrix.
- nCrt: Number of ring tertiary C(sp3.)
- C-026: R–CX–R.
- F02[C-N]: Frequency of C – N at topological distance 2.
- nHDon: Number of donor atoms for H-bonds (N and O).
- SpMax_B(m): Leading eigenvalue from Burden matrix weighted by mass.
- Psi_i_A: Intrinsic state pseudoconnectivity index – type S average.
- nN: Number of Nitrogen atoms.
- SM6_B(m): Spectral moment of order 6 from Burden matrix weighted by mass.
- nArCOOR: Number of esters (aromatic).
- nX: Number of halogen atoms.
- Mi: Mean first ionization potential (scaled on Carbon atom).
- RB_NRB: (Target) 1:ready biodegradable 0:not ready biodegradable.
Instances
Finally, the use of all instances is set.
Note that each instance contains a different chemical’s input and target variables.
The data set is divided into training, validation, and testing subsets. 60% of the instances are assigned for training, 20% for generalization, and 20% for testing.
Variables statistics
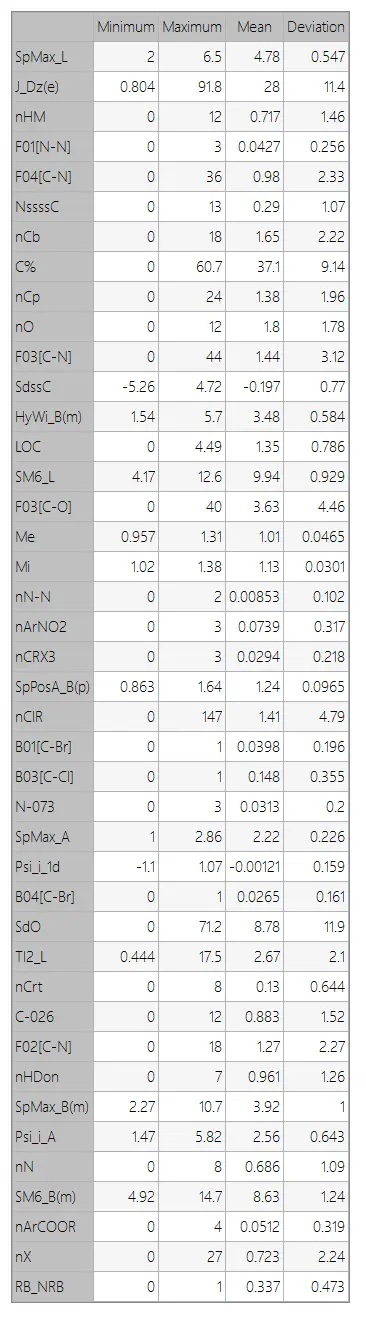
We can delve into related analytics once the data set has been established. Firstly, we examine the provided information to ensure the data is quality.
Subsequently, we calculate the data statistics, culminating in creating a table featuring the minimums, maximums, means, and standard deviations of all variables in the data set.
Variables distributions
Also, we can calculate the distributions for all variables.
The following figure shows a pie chart with the proportion of ready biodegradable (positives) and not ready biodegradable (negatives) chemicals in the data set.
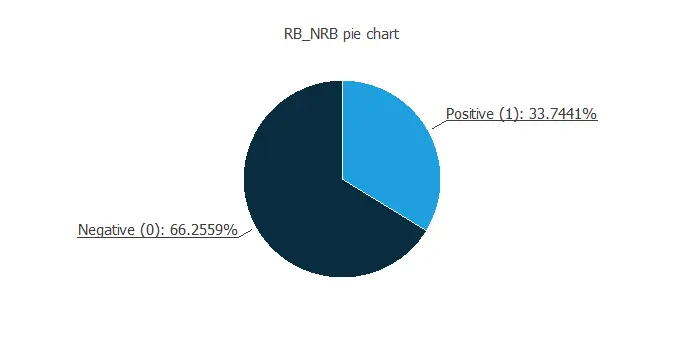
As we can see, the number of ready biodegradable chemicals is 33.7% of the samples, and not ready biodegradable represents approximately 66.3% of the samples.
Inputs-targets correlations
Finally, the inputs-targets correlations might indicate to us what factors most influence biodegradability.
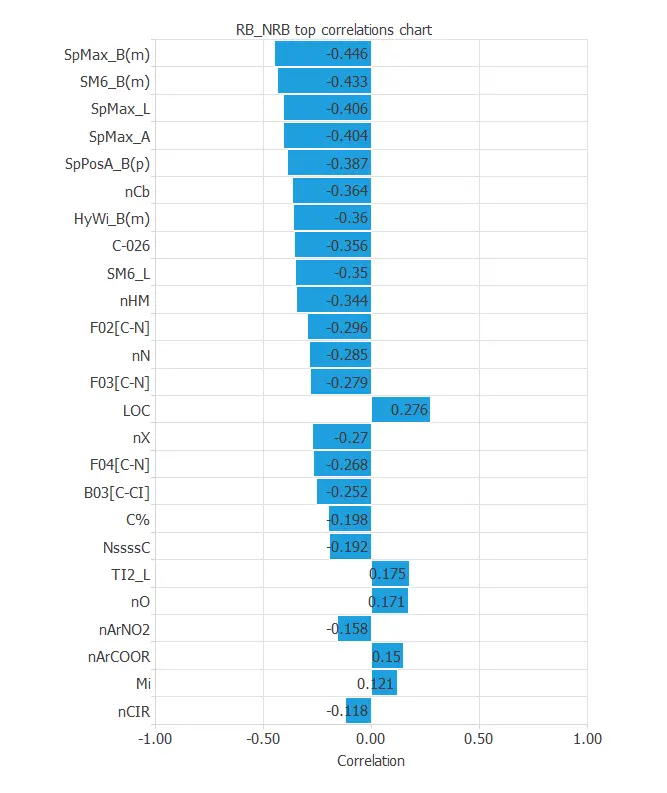
The most correlated variables are SpMax_B(m), SM6_B(m), SpMax_L, and SpMax_A, whose descriptions are above.
3. Neural network
The second step is to set a neural network representing the classification function. For this class of applications, the neural network is composed of:
- Scaling layer.
- Perceptron layers.
- Probabilistic layer.
The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables.
Here, the minimum and maximum methods have been set. Nevertheless, the mean and standard deviation method would produce very similar results.
The number of perceptron layers is 1. This perceptron layer has 41 inputs and 3 neurons.
Finally, we set the binary probabilistic method for the probabilistic layer as we want the predicted target variable to be binary.
4. Training strategy
The procedure used to carry out the learning process is called a training strategy. The training strategy is applied to the neural network to obtain the best possible performance.
The type of training is determined by how the adjustment of the parameters in the neural network takes place.
This process is composed of two terms:
- A loss index.
- An optimization algorithm.
The loss index is the mean squared error with L2 regularization. This is the default loss index for binary classification applications. The learning problem can be stated as finding a neural network that minimizes the loss index.
That is a neural network that fits the data set (error term) and does not oscillate (regularization term). The optimization algorithm that we use is the quasi-Newton method. This is also the standard optimization algorithm for this type of problem.
The following chart shows how errors decrease with the iterations during training.
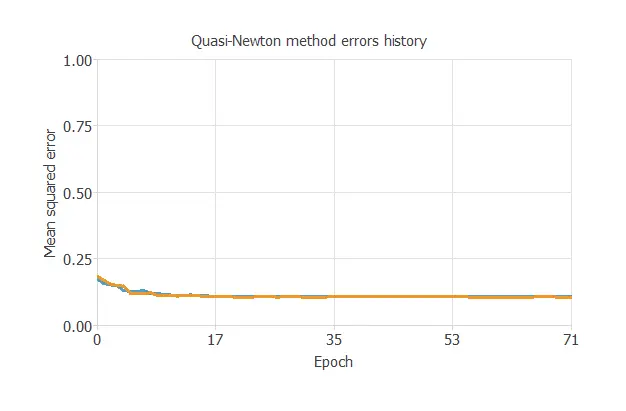
The final training and selection errors are training error = 0.108 WSE and selection error = 0.105 WSE, respectively.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties, which minimizes the error on the selected instances of the data set.
More specifically, we want to find a neural network with a selection error of less than 0.105 WSE, the value we have achieved so far.
Order selection algorithms train several network architectures with a different number of neurons and select that with the smallest selection error. The incremental order method starts with a few neurons and increases the complexity at each iteration.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network.
To validate a classification technique, we need to compare the values provided by this technique to the observed values. We can use the ROC curve as it is the standard testing method for binary classification projects.
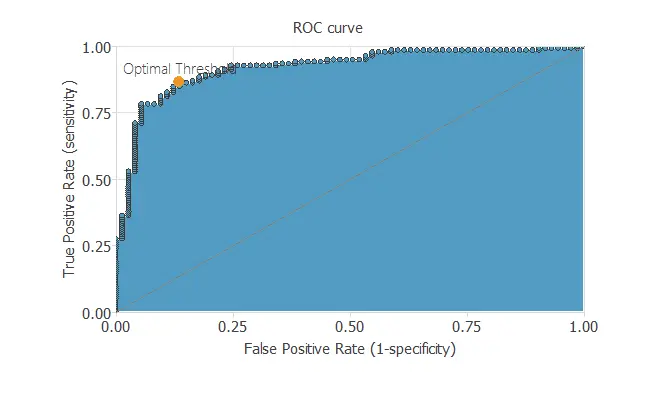
The following table contains the elements of the confusion matrix.
This matrix shows the number of negative and positive predicted values versus the real ones.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 59(28%) | 14(6.6%) |
| Real negative | 15(7.1%) | 123(58.3%) |
As we can see, the number of instances the model can correctly predict is 182 (86.3%), while it misclassifies 29 (13.7%).
Note that of all our chemical data, most are not readily biodegradable.
The binary classification tests are parameters for measuring the performance of a classification problem with two classes:
- Classification accuracy (ratio of instances correctly classified): 86.3%
- Error rate (ratio of instances misclassified): 13.7%
- Sensitivity (ratio of real positives which the model predicts as positives): 86.3%
- Specificity (ratio of real negatives which the model predicts as negatives): 86.2%
7. Model deployment
Once we test the neural network’s generalization performance, we can save the neural network for future use in the so-called model deployment mode.
We can predict if a chemical molecule can be ready or not biodegradable by calculating the neural network outputs.
For that, we need to know the input variables for them.
An example is the following: We can export the mathematical expression of the neural network, which takes inputs variables to produce output variables, in our case, to decide the biodegradability.
This classification model propagates the information through the scaling, perceptron, and probabilistic layers.
This expression is listed below.
scaled_J_Dz(e) = J_Dz(e)*(1+1)/(91.77500153-(0.8039000034))-0.8039000034*(1+1)/(91.77500153-0.8039000034)-1;
scaled_nHM = (nHM-(0.7165880203))/1.461760044;
scaled_F01[N-N] = (F01[N-N]-(0.04265400022))/0.2558889985;
scaled_F04[C-N] = (F04[C-N]-(0.9800950289))/2.331850052;
scaled_NssssC = (NssssC-(0.2900469899))/1.07325995;
scaled_C% = C%*(1+1)/(60.70000076-(0))-0*(1+1)/(60.70000076-0)-1;
scaled_nCp = (nCp-(1.376299977))/1.962589979;
scaled_nO = (nO-(1.803789973))/1.774590015;
scaled_F03[C-N] = (F03[C-N]-(1.436969995))/3.115099907;
scaled_SdssC = (SdssC-(-0.1971289963))/0.769298017;
scaled_LOC = (LOC-(1.350710034))/0.7857940197;
scaled_F03[C-O] = F03[C-O]*(1+1)/(40-(0))-0*(1+1)/(40-0)-1;
scaled_Me = Me*(1+1)/(1.31099999-(0.9570000172))-0.9570000172*(1+1)/(1.31099999-0.9570000172)-1;
scaled_Mi = Mi*(1+1)/(1.376999974-(1.021999955))-1.021999955*(1+1)/(1.376999974-1.021999955)-1;
scaled_nN-N = nN-N*(1+1)/(2-(0))-0*(1+1)/(2-0)-1;
scaled_nArNO2 = (nArNO2-(0.07393360138))/0.3173229992;
scaled_nCRX3 = (nCRX3-(0.02938389964))/0.2178940028;
scaled_nCIR = (nCIR-(1.405689955))/4.786270142;
scaled_B01[C-Br] = (B01[C-Br]-(0.03981040046))/0.1955129951;
scaled_B03[C-CI] = (B03[C-CI]-(0.1478669941))/0.3549689949;
scaled_N-073 = (N-073-(0.03127960116))/0.1994490027;
scaled_Psi_i_1d = Psi_i_1d*(1+1)/(1.072999954-(-1.098999977))+1.098999977*(1+1)/(1.072999954+1.098999977)-1;
scaled_B04[C-Br] = B04[C-Br]*(1+1)/(1-(0))-0*(1+1)/(1-0)-1;
scaled_SdO = SdO*(1+1)/(71.16699982-(0))-0*(1+1)/(71.16699982-0)-1;
scaled_TI2_L = TI2_L*(1+1)/(17.53700066-(0.4440000057))-0.4440000057*(1+1)/(17.53700066-0.4440000057)-1;
scaled_nCrt = (nCrt-(0.1298580021))/0.6437550187;
scaled_F02[C-N] = (F02[C-N]-(1.274880052))/2.272919893;
scaled_nHDon = (nHDon-(0.9611369967))/1.256420016;
scaled_Psi_i_A = (Psi_i_A-(2.558419943))/0.6424599886;
scaled_nN = (nN-(0.6862559915))/1.089869976;
scaled_nArCOOR = (nArCOOR-(0.05118479952))/0.3188149929;
scaled_nX = (nX-(0.723222971))/2.238219976;
perceptron_layer_0_output_0 = logistic[ -0.177432 + (scaled_J_Dz(e)*0.0855846)+ (scaled_nHM*-1.24226)+ (scaled_F01[N-N]*-0.283113)+ (scaled_F04[C-N]*-0.35339)+ (scaled_NssssC*-0.856399)+ (scaled_C%*-0.139905)+ (scaled_nCp*-0.289111)+ (scaled_nO*-0.20023)+ (scaled_F03[C-N]*-0.322568)+ (scaled_SdssC*0.132424)+ (scaled_LOC*0.360906)+ (scaled_F03[C-O]*-0.303221)+ (scaled_Me*0.154041)+ (scaled_Mi*0.187736)+ (scaled_nN-N*0.125482)+ (scaled_nArNO2*-0.448966)+ (scaled_nCRX3*-0.221001)+ (scaled_nCIR*-0.511291)+ (scaled_B01[C-Br]*-0.111304)+ (scaled_B03[C-CI]*-0.116656)+ (scaled_N-073*0.139527)+ (scaled_Psi_i_1d*-0.103048)+ (scaled_B04[C-Br]*0.176509)+ (scaled_SdO*0.540496)+ (scaled_TI2_L*0.414255)+ (scaled_nCrt*-0.302632)+ (scaled_F02[C-N]*-0.031898)+ (scaled_nHDon*-0.120617)+ (scaled_Psi_i_A*0.698333)+ (scaled_nN*-0.467465)+ (scaled_nArCOOR*0.454082)+ (scaled_nX*-0.336846) ];
perceptron_layer_0_output_1 = logistic[ 0.190828 + (scaled_J_Dz(e)*-0.106789)+ (scaled_nHM*1.33593)+ (scaled_F01[N-N]*0.309528)+ (scaled_F04[C-N]*0.369096)+ (scaled_NssssC*0.920219)+ (scaled_C%*0.146187)+ (scaled_nCp*0.320681)+ (scaled_nO*0.299069)+ (scaled_F03[C-N]*0.339289)+ (scaled_SdssC*-0.148324)+ (scaled_LOC*-0.407062)+ (scaled_F03[C-O]*0.345641)+ (scaled_Me*-0.172198)+ (scaled_Mi*-0.203953)+ (scaled_nN-N*-0.133797)+ (scaled_nArNO2*0.463928)+ (scaled_nCRX3*0.241401)+ (scaled_nCIR*0.564473)+ (scaled_B01[C-Br]*0.105944)+ (scaled_B03[C-CI]*0.109147)+ (scaled_N-073*-0.151173)+ (scaled_Psi_i_1d*0.118023)+ (scaled_B04[C-Br]*-0.19303)+ (scaled_SdO*-0.585528)+ (scaled_TI2_L*-0.428076)+ (scaled_nCrt*0.309396)+ (scaled_F02[C-N]*0.0309882)+ (scaled_nHDon*0.121517)+ (scaled_Psi_i_A*-0.760547)+ (scaled_nN*0.496675)+ (scaled_nArCOOR*-0.487881)+ (scaled_nX*0.353319) ];
pprobabilistic_layer_combinations_0 = -0.0876607 +2.58938*perceptron_layer_0_output_0 -2.83917*perceptron_layer_0_output_1
RB_NRB = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);
logistic(x){
return 1/(1+exp(-x))
}
Conclusions
References
- We have obtained the data for this problem from the UCI Machine Learning Repository.
- Mansouri, K., Ringsted, T., Ballabio, D., Todeschini, R., Consonni, V. (2013). Quantitative Structure – Activity Relationship models for ready biodegradability of chemicals. Journal of Chemical Information and Modeling, 53, 867-878.



