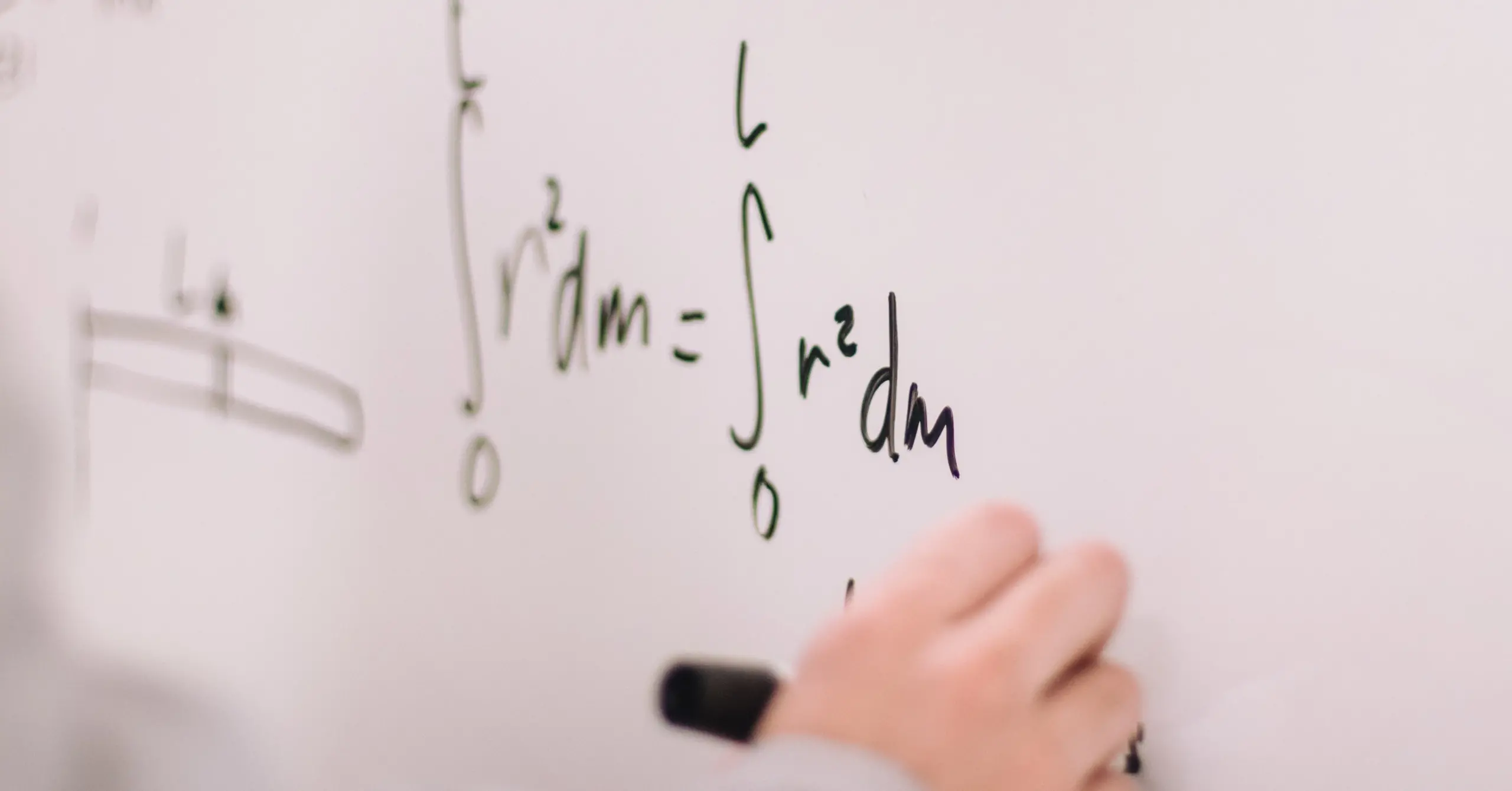This post focuses on testing analysis methods for binary classification models.
Once a machine learning model has been built, it is needed to evaluate its generalization capabilities. Testing analysis aims to compare the model’s responses against data that it has never seen before. This process simulates what would happen in a real-world situation. In this regard, the testing results determine if the model is good enough to be moved into the deployment phase. The testing methods to be used depend on the type of model with which we are working.
Indeed, testing methods for approximation are different from those for classification. Moreover, different testing methods are used for binary classification and multiple classifications.
Contents
- Testing data.
- 1. Confusion matrix.
- 2. Binary classification tests.
- 3. ROC curve.
- 4. Positive and negative rates.
- 5. Cumulative gain.
- 6. Lift chart.
- Conclusions.
Neural Designer implements all those testing methods. You can download this data science and machine learning platform here to try them in practice.
Testing data
To illustrate those testing methods for binary classification, we generate the following testing data.
| Instance | Target | Output | Instance | Target | Output |
|---|---|---|---|---|---|
| 1 | 1 | 0.99 | 11 | 1 | 0.41 |
| 2 | 1 | 0.85 | 12 | 0 | 0.40 |
| 3 | 1 | 0.70 | 13 | 0 | 0.28 |
| 4 | 1 | 0.60 | 14 | 0 | 0.27 |
| 5 | 0 | 0.55 | 15 | 0 | 0.26 |
| 6 | 1 | 0.54 | 16 | 0 | 0.25 |
| 7 | 0 | 0.53 | 17 | 0 | 0.24 |
| 8 | 1 | 0.52 | 18 | 0 | 0.23 |
| 9 | 0 | 0.51 | 19 | 0 | 0.20 |
| 10 | 1 | 0.49 | 20 | 0 | 0.10 |
The target column determines whether an instance is negative (0) or positive (1). The output column is the model’s corresponding score, i.e., the probability that the corresponding instance is positive.
1. Confusion matrix
The confusion matrix is a visual aid to depict the performance of a binary classifier. The first step is to choose a decision threshold τ to label the instances as positives or negatives. If the probability assigned to the instance by the classifier is higher than &tau, it is labeled as positive; if it is lower, it is labeled as negative. The default value for the decision threshold is τ = 0.5. Once all the testing instances are classified, the output labels are compared against the target labels. This gives us four numbers:
- True positives (TP): Number of instances that are positive and are classified as positive.
- False positives (FP): Number of instances that are negative and are classified as positive.
- False negatives (FN): Number of instances that are positive and are classified as negative.
- True negatives (TN): Number of instances that are negative and are classified as negative.
The confusion matrix then takes the following form:
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | true positives | false negatives |
| Real negative | false positives | false negatives |
As we can see, the rows represent the target classes, while the columns represent the output classes. The diagonal cells show the number of correctly classified cases, and the off-diagonal cells show the misclassified instances. In our example, let us choose a decision threshold τ = 0.5. After labeling the outputs, the number of true positives is 6, the number of false positives is 3, the number of false negatives is 2, and the number of true negatives is 9. This information is arranged in the confusion matrix as follows.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 6 | 2 |
| Real negative | 3 | 9 |
As we can see, the model classifies most of the cases correctly. However, we must perform a more exhaustive testing analysis to understand its generalization capabilities fully.
2. Binary classification tests
The binary classification tests are parameters derived from the confusion matrix, which can help understand the information it provides. Some of the most crucial binary classification tests are parameters are the following:
Classification accuracy, which is the ratio of instances correctly classified, $$ classification\_accuracy = \frac{true\_positives+true\_negatives}{total\_instances}$$
Error rate, which is the ratio of instances misclassified, $$ error\_rate = \frac{false\_positives+false\_negatives}{total\_instances}$$
Sensitivity, which is the portion of actual positives that are predicted as positives, $$ sensitivity = \frac{true\_positives}{positive\_instances}$$
Specificity, which is the portion of actual negatives predicted as negative, is calculated as follows: $$ specificity = \frac{true\_negatives}{negative\_instances}$$
In our example, the accuracy is 0.75 (75%), and the error rate is 0.25 (25%), so the model can correctly label many instances. The sensitivity is 0.75 (75%), meaning the model can detect the positive instances. Finally, the specificity is 0.75 (75%), which shows that the model correctly labels most negative instances.
4. ROC curve
The receiver operating characteristic, or ROC curve, is one of the most helpful testing analysis methods for binary classification problems. Indeed, it provides a comprehensive and visual way to summarize the accuracy of a classifier. By varying the value of the decision threshold between 0 and 1, we obtain a set of different classifiers to calculate their specificity and sensitivity.
The ROC curve’s points represent the values of those parameters for each value of the decision threshold. The False Positive rate (or 1-specificity) values are plotted on the x-axis, while the corresponding True Positive Rate (or sensitivity) values are plotted on the y-axis. The ROC curve is illustrated in the following figure.
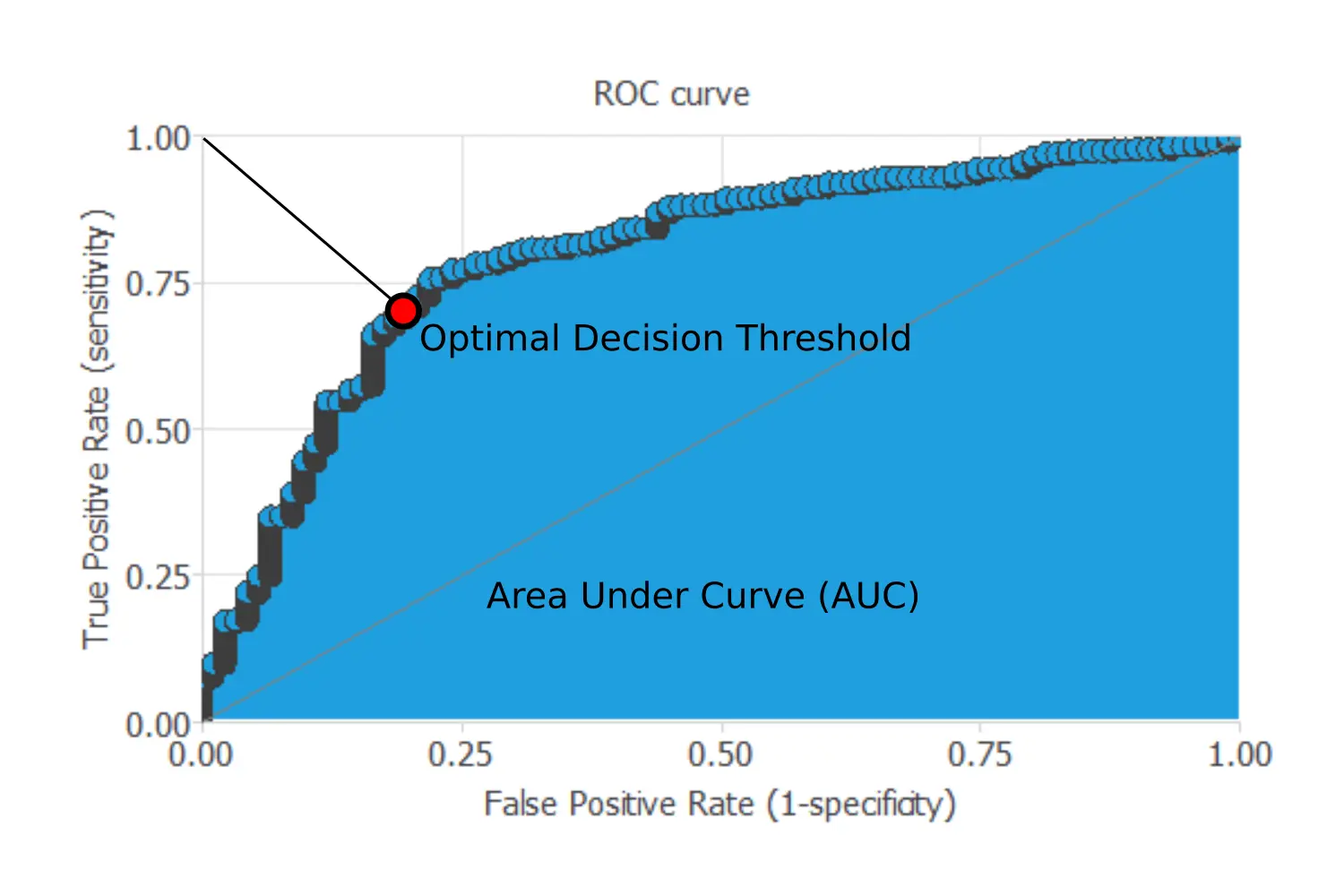
For a perfect model, the ROC curve passes through the upper left corner, where the sensitivity and the specificity are 1. Consequently, the closer to the point (0,1) of the ROC curve, the better the classifier. The most critical parameter obtained from a ROC curve is the area under the curve (AUC), which measures the classifier’s quality.
For a perfect model, the area under the curve is 1. Besides, we can find the optimal decision threshold, which is the threshold that best discriminates between the two different classes as it maximizes the specificity and the sensitivity. Its value will be the threshold’s value corresponding to the ROC curve point closer to the upper left corner. The following chart shows the ROC curve for our example.
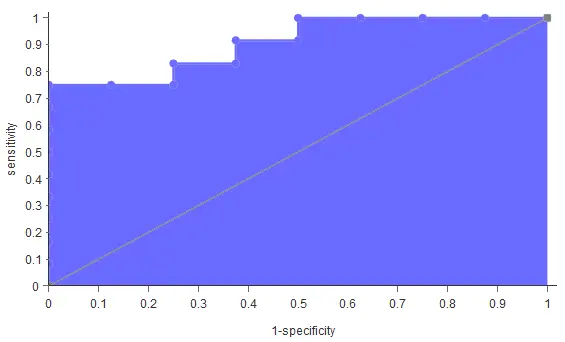
For our example, the area under the curve (AUC) is 0.90, which shows that our classifier performs well. On the other hand, the optimal decision threshold (that best separates the two classes) is 0.4.
3. Positive and negative rates
Positive and negative rates measure the percentage of cases that perform the desired action. In marketing applications, the positive rate is called the conversion rate. Indeed, it depicts the number of clients that respond positively to our campaign out of the number of contacts. The best way to illustrate this method is by returning to our example. The following chart shows three rates. The first pair of columns shows the data set’s initial rate of positives and negatives. In this case, we have 40% of positives and 60% of negatives. The pair of columns in the middle shows this rate for the predicted instances as positives. Within this group, the percentage of positives is 66.7%, and the percentage of negatives is 33.4%. Lastly, the two columns on the right represent the analogous information for the predicted instances as negatives. We have 81.9% of negatives and 18.1% of positives in this case. Our model then multiplies the positive rates of the actual data by 1.66 and multiplies the negative rates by 1.365.
5. Cumulative gain
While the previous methods evaluated the model’s performance on the whole population, cumulative gain charts assess the classifier’s performance on every data portion. This testing method is beneficial in those problems where the objective is to find more positive instances by studying the least amount of them, such as a marketing campaign.
As we have said, the classifier labels each case with a score, which is the probability that the current instance is positive. Consequently, if the model can correctly rank the instances, by first calling those with the highest scores, we achieve more positive responses as opposed to randomness. Cumulative gain charts visually show this advantage. The following chart shows the results of the cumulative gain analysis for our example. The grey line or baseline in the middle represents the cumulative gain for a random classifier, while the blue line is the cumulative gain for our example. Each point represents the percentage of positives found for the corresponding ratio of instances written on the x-axis.
Finally, the negative cumulative gain is also depicted by the red line. This one shows the percentage of negatives found for each data portion. If we have a good classifier, the cumulative gain should be above the baseline, while the negative cumulative gain should be below it, as in our example. Supposing our example was a marketing campaign, the curve shows that we would have gotten all the positive responses by calling only 60% of the population with the highest scores.
Once all the curves are plotted, we can calculate the maximum gain score, the maximum distance between the cumulative gain and the negative cumulative gain, and the point of maximum gain, which is the percentage of the instances for which the score has been reached.
Once all the curves are plotted, we can calculate the maximum gain score, the maximum distance between the cumulative gain and the negative cumulative gain. We can also calculate the point of maximum gain, the percentage of instances for which the score has been reached.
| Instances ratio | 0.6 |
|---|---|
| Maximum gain score | 0.667 |
As shown in the table, the maximum distance between both lines is reached by 60% of the population and takes the value of 0.667.
6. Lift chart
The information provided by lift charts is closely related to that provided by the cumulative gain. It represents the actual lift for each population percentage, the ratio between positive instances found using and not using the model. The lift chart for a random classifier is represented by a straight line joining the points (0,1) and (1,1). The lift chart for the current model is constructed by plotting different population percentages on the x-axis against its corresponding actual lift on the y-axis. If the lift chart keeps above the baseline, the model is better than randomness for every point. Back to our example, the lift chart is shown below.
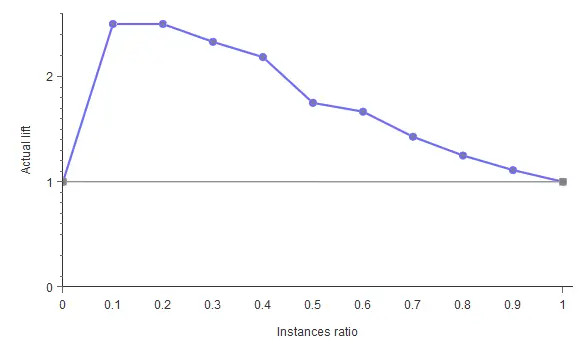
As shown, the lift curve always stays above the grey line, reaching its maximum value of 2.5 for the instance ratios of 0.1 and 0.2. That means that the model multiplies the percentage of positives found by 2.5 for the 10% and 20% of the population.
Conclusions
Testing a model is critical for knowing a model’s performance. This article has provided six different methods to test your binary models. All these testing methods are available in the machine learning software Neural Designer.