This study aims to classify different raisins using machine learning.
Several traditional methods exist for assessing and determining the raisin type, but they can be time-consuming and tedious. To solve this problem, we can use machine learning to classify the different types of raisins and thus facilitate the treatment of the raisins.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
This example is solved with Neural Designer. To follow it step by step, you can use the free trial.
1. Application type
We will predict between two types of raisins, so the variable to be predicted is binary (Kecimen or Besni). Therefore this is a classification project.
The goal here is to model the type of raisin according to the features of the raisin for his subsequent use.
2. Data set
The first step is to prepare the data set, which is the source of information for the problem. We need to configure three things here:
- Data source.
- Variables.
- Instances.
Data source
The data file raisin_dataset.csv contains the data for this example. A total of 900 raisins were used, including 450 from both varieties and seven features were extracted. Here the number of variables (columns) is 8, and the number of instances (rows) is 900.
Variables
The features or variables are the following:
- Area: Gives the number of pixels within the boundaries of the raisin.
- Perimeter: It measures the environment by calculating the distance between the boundaries of the raisin and the pixels around it.
- MajorAxisLenght: Gives the length of the main axis, which is the longest line that can be drawn on the raisin.
- MinorAxisLenght: Gives the length of the small axis, which is the shortest line that can be drawn on the raisin.
- Eccentricity: It gives a measure of the eccentricity of the ellipse, which has the same moments as raisins.
- ConvexArea: Gives the number of pixels of the smallest convex shell of the region formed by the raisin.
- Extent: It gives the ratio of the region formed by the raisin to the total pixels in the bounding box.
- Class: Kecimen and Besni raisin.
All variables in the study are inputs, except ‘Class’, which is the output that we want to extract for this machine learning study. Note that ‘Class’ is binary and only takes the values Kecimen and Besni.
Instances
The instances are divided into training, selection, and testing subsets. They represent 540 (60%), 180 (20%) and 180 (20%) of the original instances, respectively, and are split at random.
Once the data set has been set, we can perform a few related analytics. First, we check the provided information and ensure that the data is of good quality.
Variables distributions
The data distributions tell us the percentages of Kecimen and Besni raisin.
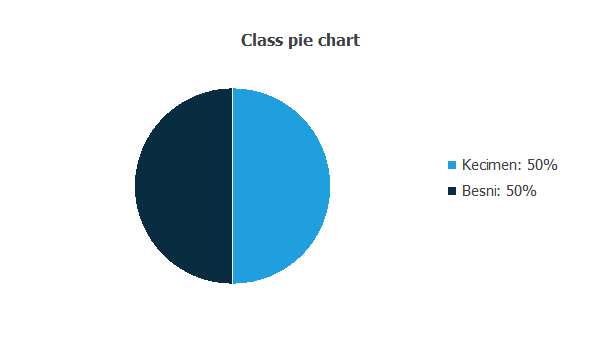
In this data set, there are the same numbers of samples of both categories (Kecimen and Besni).
Inputs-targets correlations
The inputs-targets correlations might indicate to us what factors are more influence.
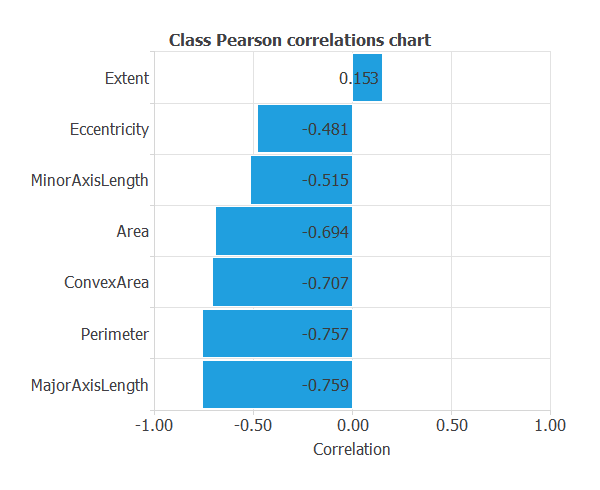
From the above chart, we can see that all the features have a significant influence except the ‘Extent’ in comparison with the others.
3. Neural network
The second step is to choose a neural network to represent the classification function. For classification problems, it is composed of:
The scaling layer contains the statistics on the input calculated from the data file and the method for scaling the input variables. Here the minimum and maximum scaling methods are set, but the mean and standard deviation scaling method produce similar results.
We set one perceptron layer, with 3 neurons as a first guess, having the hyperbolic tangent (tanh) as the activation function.
The next figure is a diagram for the neural network used in this example.
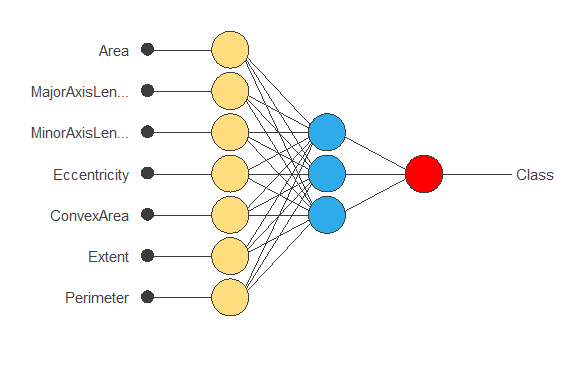
The yellow circles represent scaling neurons, the blue circles perceptron neurons, and the red circles probabilistic neurons. The number of inputs is 7, and the number of outputs is 1.
4. Training strategy
The training strategy is applied to the neural network to obtain the best possible performance. It is composed of two things:
- A loss index.
- An optimization algorithm.
The selected loss index is the normalized squared error (NSE) with L2 regularization. The normalized squared error is helpful in applications where the targets are balanced, as in this case.
The error term fits the neural network to the training instances of the data set. The regularization term makes the model more stable and improves generalization, so our model will be more predictive.
The selected optimization algorithm that minimizes the loss index is the quasi-Newton method.
The following chart shows how the training (blue) and selection (orange) errors decrease with the training epochs.
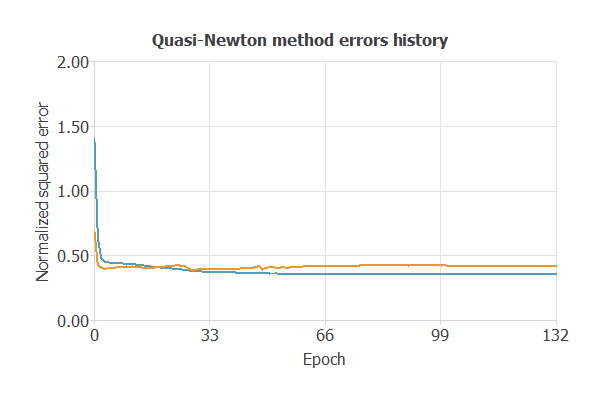
The final training and selection errors are training error = 0.353 NSE (blue) and selection error = 0.419 NSE (orange), respectively. The following section will improve the generalization performance by reducing the selection error.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties. That is, we want to improve the final selection error obtained before (0.419 NSE).
The best selection error is achieved using a model whose complexity is the most appropriate to produce a better data fit. Order selection algorithms are responsible for finding the optimal number of perceptron neurons in the neural networks.
The following chart shows the error history for different numbers of perceptron neurons. We conclude that for two neurons, the selection error is the minimum.
.webp)
The chart shows that the optimal number of neurons is 2, with selection error = 0.398 NSE.
The following figure shows the final network architecture for this application.
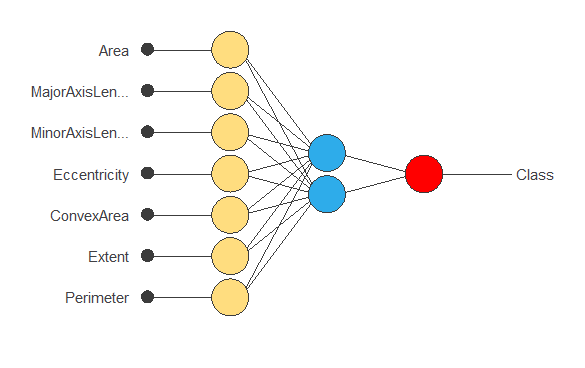
6. Testing analysis
The next step is to perform an exhaustive testing analysis to validate the neural network’s predictive capabilities. The testing compares the values provided by this technique to the observed values.
A good measure of the precision of a binary classification model is the ROC curve. Furthermore, the ROC curve analysis returns the optimal value for decision threshold = 0.63.
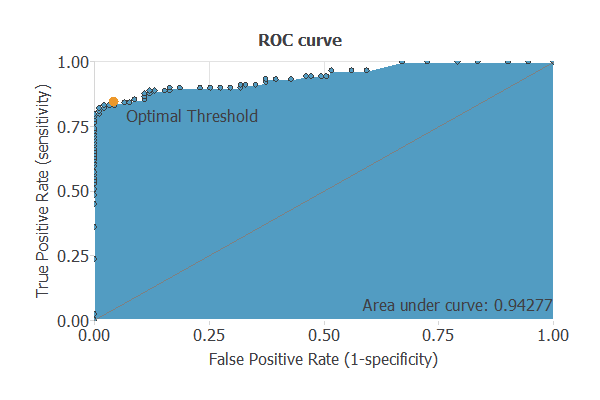
We are interested in the area under the curve (AUC). A perfect classifier would have an AUC=1, and a random one would have an AUC=0.5.
Our model has an AUC = 0.942, which is a good indicator of our model.
We can also look at the confusion matrix. Next, we show the elements of this matrix for a decision threshold = 0.63.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 87 (48.3%) | 4 (2.2%) |
| Real negative | 14 (7.8%) | 75 (41.7%) |
From the above confusion matrix, we can calculate the following binary classification tests:
- Classification accuracy: 90% (ratio of correctly classified samples).
- Error rate: 10% (ratio of misclassified samples).
- Sensitivity: 95.6% (percentage of actual positive classified as positive).
- Specificity: 84.26% (percentage of actual negative classified as negative).
7. Model deployment
Once we have tested the raisin model classification, we can use it to evaluate the probability selection:
For instance, consider a raisin with the following features:
- Area: 80804.1
- MajorAxisLenght: 410.93
- MinorAxisLenght: 224.488
- Eccentricity: 86186.1
- ConvexArea: 86186.1
- Extent: 0.599
- Perimeter: 1005.91
- Class(1=Kecimen): 0.915
The probability of Kecimen for this raisin is: 91.5%.
We can export the mathematical expression of the neural network to any factory of raisin to facilitate the work of classification.
This expression is listed below.
scaled_Area = (Area-87804.10156)/38980.39844;
scaled_MajorAxisLength = (MajorAxisLength-430.9299927)/115.9710007;
scaled_MinorAxisLength = (MinorAxisLength-254.4880066)/49.96110153;
scaled_Eccentricity = (Eccentricity-0.7815420032)/0.09026820213;
scaled_ConvexArea = (ConvexArea-91186.10156)/40746.60156;
scaled_Extent = (Extent-0.6995080113)/0.05343849957;
scaled_Perimeter = (Perimeter-1165.910034)/273.6119995;
perceptron_layer_1_output_0 = tanh( 0.625073 + (scaled_Area*0.47795) + (scaled_MajorAxisLength*0.54666) + (scaled_MinorAxisLength*0.222985) + (scaled_Eccentricity*0.277638) + (scaled_ConvexArea*0.506997) + (scaled_Extent*0.77402) + (scaled_Perimeter*1.16189) );
perceptron_layer_1_output_1 = tanh( 0.661286 + (scaled_Area*0.00797501) + (scaled_MajorAxisLength*-0.703279) + (scaled_MinorAxisLength*-0.0445966) + (scaled_Eccentricity*0.069447) + (scaled_ConvexArea*-0.392766) + (scaled_Extent*-0.24135) + (scaled_Perimeter*-1.36504) );
perceptron_layer_1_output_2 = tanh( -0.0796286 + (scaled_Area*1.34031) + (scaled_MajorAxisLength*0.191064) + (scaled_MinorAxisLength*0.612609) + (scaled_Eccentricity*0.207755) + (scaled_ConvexArea*-0.557862) + (scaled_Extent*-0.0264986) + (scaled_Perimeter*-2.60166) );
probabilistic_layer_combinations_0 = -0.90159 +0.58348*perceptron_layer_1_output_0 +1.53865*perceptron_layer_1_output_1 +3.4659*perceptron_layer_1_output_2
Class = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0) );
In conclusion, we have to build a predictive model to determine the kind of raisin.

