Contents

1. Application type.
2. Data set.
3. Neural network.
4. Training strategy.
5. Model selection.
6. Testing analysis.
7. Model deployment.

This example is solved with Neural Designer. To follow it step by step, you can use the free trial.

1. Application type

This is an approximation project since the variable to be predicted is continuous (wine quality).

The fundamental goal here is to model the quality of a wine as a function of its features.

2. Data set

The data file wine_quality.csv contains a total of 1599 rows and 12 columns. The first row in the data file contains the names of the variables, and the rest represent the instances.

The data set contains the following variables:

• fixed_acidity
• volatile_acidity
• citric_acid
• residual_sugar
• chlorides
• free_sulfur_dioxide
• total_sulfur_dioxide
• density
• pH
• sulfates
• alcohol
• quality

On the other hand, the instances are divided randomly into training, selection, and testing subsets, containing 60%, 20%, and 20% of the instances, respectively.

We will run a few related tasks once the data set page has been edited. With that, we check that the provided information is of good quality.

We can calculate the data distributions and draw a histogram for each variable to see how they are distributed. The following figure shows the histogram for the quality data, which is the only target.

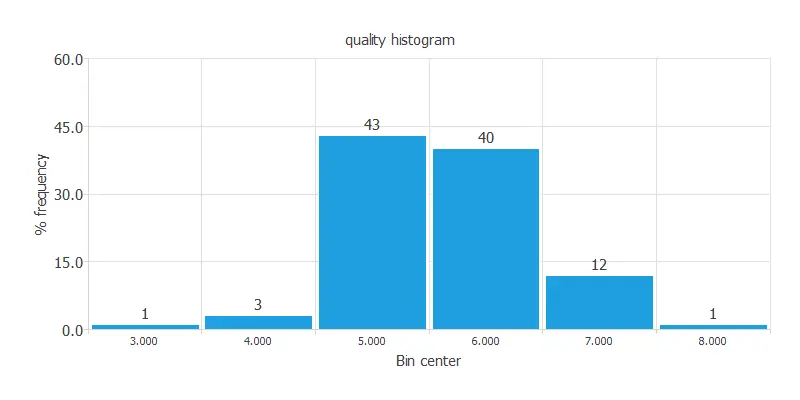
As we can see, the target variable is unbalanced since there are many quality scores around six and much less with values near 0 or 10. This will result in a poor-quality model.

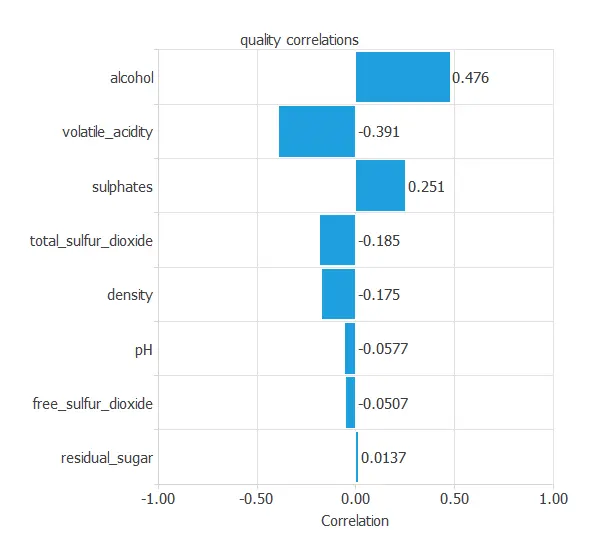
The following chart shows the correlations of the input variables with the target variable.

3. Neural network

The second step is to set the neural network stuff. For approximation project types, it typically consists of:

• Scaling layer.
• Perceptron layers.
• Unscaling layer.
• Bounding layer.

The scaling layer section contains the statistics on the inputs calculated from the data file and the method for scaling the input variables. Here, the mean and standard deviation scaling method has been set. Nevertheless, the mean and standard deviation methods would produce very similar results.

In this problem, we will use a hidden layer and a linear output layer of perceptrons, the default approximation. It must have ten inputs and one output neuron. While the problem constrains inputs and output neurons, the number of neurons in the hidden layer is a design variable. Here, we use three neurons in the hidden layer, yielding 37 parameters. Finally, we randomly initialize all the biases and synaptic weights in the neural network.

The unscaling layer contains the statistics on the outputs calculated from the data file and the method for unscaling the output variables. Here, the minimum and maximum unscaling methods will be used.

Lastly, we will use a bounding layer in this example, with 1 and 10 as the lower and upper bounds, respectively. The quality variable’s value clearly defines lower and upper limits.

You can represent the neural network for this example in the following diagram:

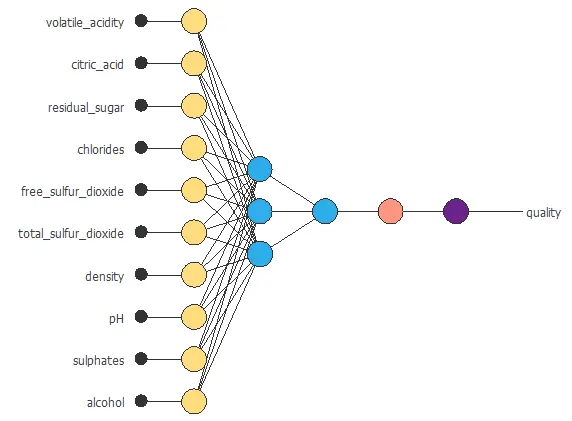
The function above is parameterized by all the biases and synaptic weights in the neural network, i.e., 37 parameters.

4. Training strategy

The next step is selecting an appropriate training strategy to define what the neural network will learn. A general training strategy for approximation consists of two components:

• A loss index.
• An optimization algorithm.

The loss index chosen for this problem is the normalized squared error between the neural network outputs and the data set’s targets. On the other hand, we apply L2 regularization with weak weight in this case.

The selected optimization algorithm is the quasi-Newton method.

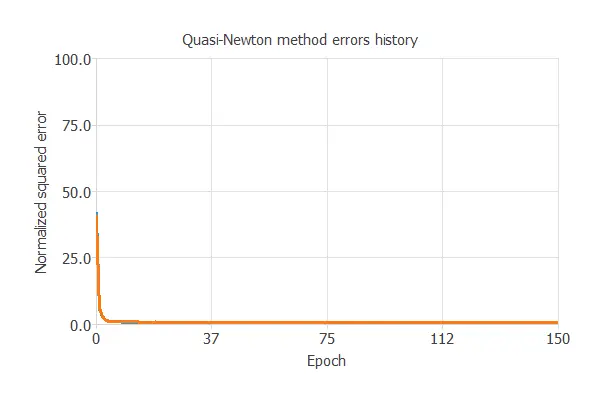
The most crucial training result is the final selection error. Indeed, this is a measure of the generalization capabilities of the neural network. Here, the final selection error is selection error = 0.678 NSE.

5. Model selection

The objective of model selection is to find the network architecture with the best generalization properties, which minimizes the error on the selected instances of the data set.

More specifically, we want to find a neural network with a selection error of less than 0.678 NSE, which is the value we have achieved.

Order selection algorithms train several network architectures with a different number of neurons and select that with the smallest selection error.

The incremental order method starts with a few neurons and increases the complexity at each iteration. The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.

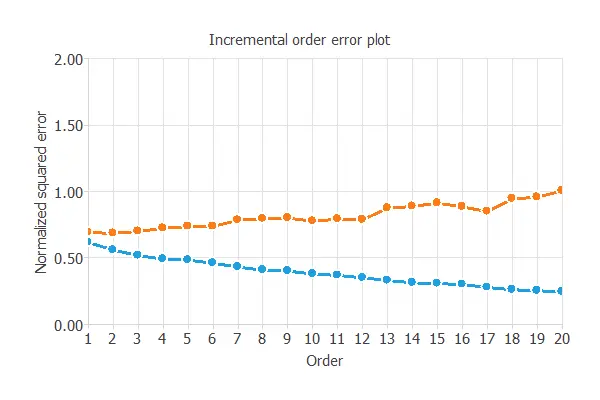
The final selection error achieved is 0.661 for an optimal number of neurons of 1.

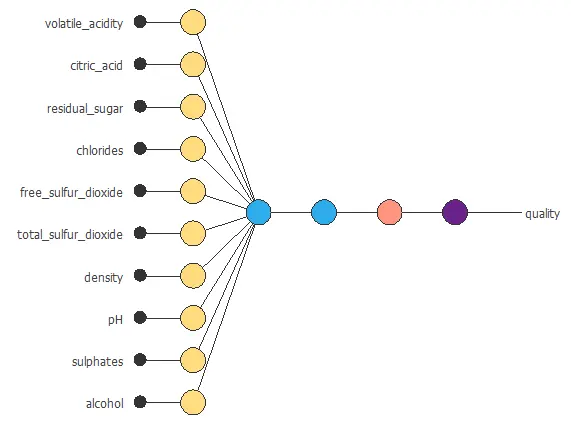
The graph above represents the architecture of the final neural network.

6. Testing analysis

A standard method for testing the prediction capabilities is to compare the neural network outputs against an independent data set. The linear regression analysis leads to 3 parameters for each output: intercept, slope, and correlation. The next figure shows the results of this analysis.

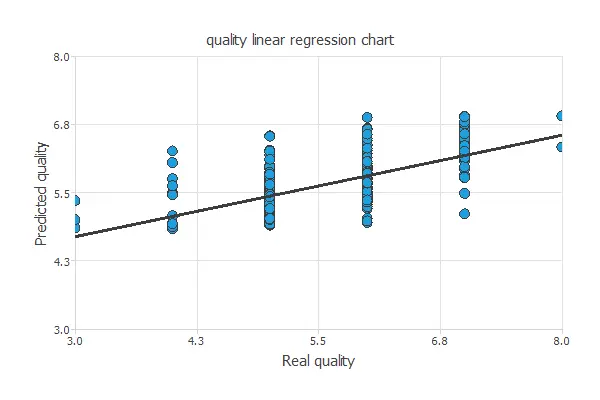
If the correlation is equal to 1, then there is a perfect correlation between the outputs from the neural network and the targets in the testing subset. For this case, the correlation has an R2 = 0.58, which indicates that the model is not predicting very well.

As mentioned earlier, the data quality exhibits a significant imbalance, as evident from the preceding graph.

7. Model deployment

After all the steps, we haven’t achieved the best possible model. Nevertheless, it is still better than guessing randomly.

The next listing shows the mathematical expression of the predictive model.

scaled_volatile_acidity = (volatile_acidity-0.527821)/0.17906;
scaled_citric_acid = (citric_acid-0.270976)/0.194801;
scaled_residual_sugar = (residual_sugar-2.53881)/1.40993;
scaled_chlorides = (chlorides-0.0874665)/0.0470653;
scaled_free_sulfur_dioxide = (free_sulfur_dioxide-15.8749)/10.4602;
scaled_total_sulfur_dioxide = (total_sulfur_dioxide-46.4678)/32.8953;
scaled_density = (density-0.996747)/0.00188733;
scaled_pH = (pH-3.31111)/0.154386;
scaled_sulfates = (sulfates-0.658149)/0.169507;
scaled_alcohol = (alcohol-10.423)/1.06567;
y_1_1 = tanh (-0.271612+ (scaled_volatile_acidity*-0.313035)+ (scaled_citric_acid*-0.124956)+ (scaled_residual_sugar*0.00194975)+ (scaled_chlorides*-0.0802881)+ (scaled_free_sulfur_dioxide*0.0392384)+ (scaled_total_sulfur_dioxide*-0.111936)+ (scaled_density*0.0456105)+ (scaled_pH*-0.11043)+ (scaled_sulfates*0.122299)+ (scaled_alcohol*0.361693));
scaled_quality =  (0.159294+ (y_1_1*0.453138));
quality = (0.5*(scaled_quality+1.0)*(8-3)+3);
quality = max(1, quality)
quality = min(10, quality)

You can export the formula below to the software tool the customer requires.

References

• P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis. Modeling wine preferences by data mining from physicochemical properties. In Decision Support Systems, Elsevier, 47(4):547-553, 2009.

Related posts