In this example, we build a machine learning model to calculate water toxicity using actual data from a water body.
Thank you for reading this post, don't forget to subscribe!Many chemicals partition into water and can exert adverse effects on aquatic systems, threatening the survival of the organisms that inhabit these ecosystems.
Calculating a standard measure of aquatic toxicity is a lengthy and costly procedure.
As a result, we do not need to measure it in the laboratory.
This example is solved with Neural Designer. You can use the free trial to understand how the solution is achieved step by step.
Contents
1. Application type
This is an approximation project since the variable to be predicted is continuous.
The primary objective is to model the LC50 (the standard measure of toxicity) as a function of the sample’s molecular properties.
2. Data set
The first step is to prepare the data set. This is the source of information for the approximation problem. It is composed of:
- Data source.
- Variables.
- Instances.
Data set
The file aquatic-toxicity.csv contains the data for this example. Here, the number of variables (columns) is 9, and the number of instances (rows) is 546.
Variables
We have the following variables for this analysis:
Molecular descriptors (input variables)
- TPSA – Topological polar surface area (N, O, P, S atoms considered).
- SAacc – Van der Waals surface area of hydrogen bond acceptor atoms.
- H-050 – Number of hydrogen atoms bonded to heteroatoms.
- MLOGP – Octanol–water partition coefficient (LogP) from the Moriguchi model.
- RDCHI – Topological index encoding molecular size and branching (ignores heteroatoms).
- GATS1p – Descriptor encoding molecular polarizability.
- nN – Number of nitrogen atoms in the molecule.
- C-040 – Number of carbon atoms of type R–C(=X)–X / R–C#X / X=C=X (X = electronegative atom such as O, N, S, P, Se, halogens).
Target variable
LC50 – Standard toxicity measure: mean lethal concentration (−Log(mol/L)).
Instances
The instances are randomly split into 60% for training, 20% for validation, and 20% for testing.
Variables distributions
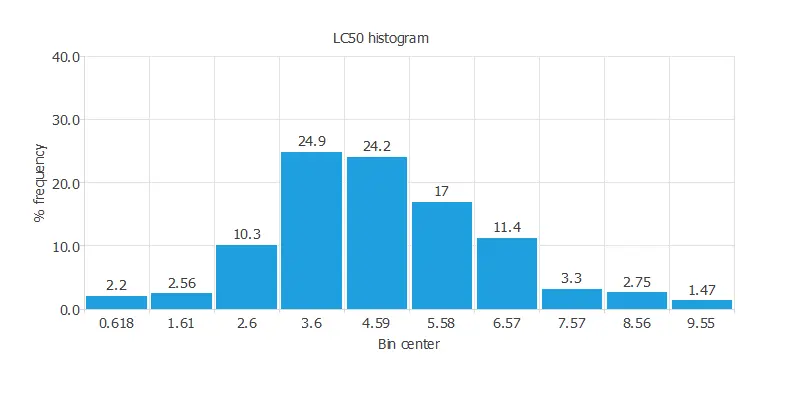
Calculating the data distributions helps us verify the accuracy of the available information and identify anomalies.
The following chart shows the histogram for the power-generated variable:
Inputs-targets correlations
It is also interesting to look for dependencies between input and target variables.
To do that, we can plot an input-target correlations chart.
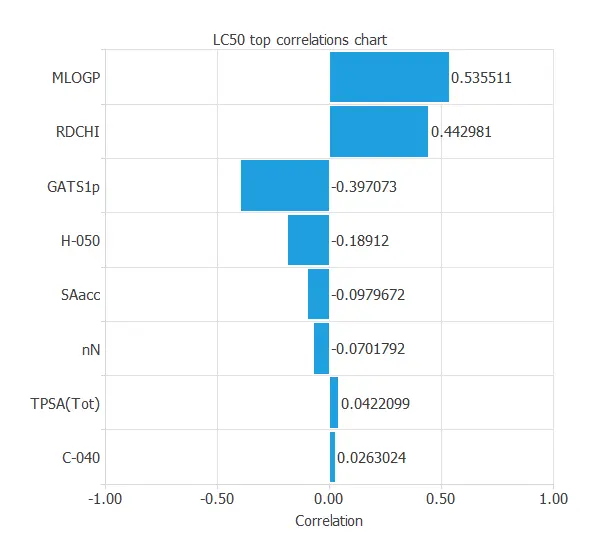
MLOGP and RDCHI are the most correlated variables because they measure lipophilicity, which is the driving force of narcosis.
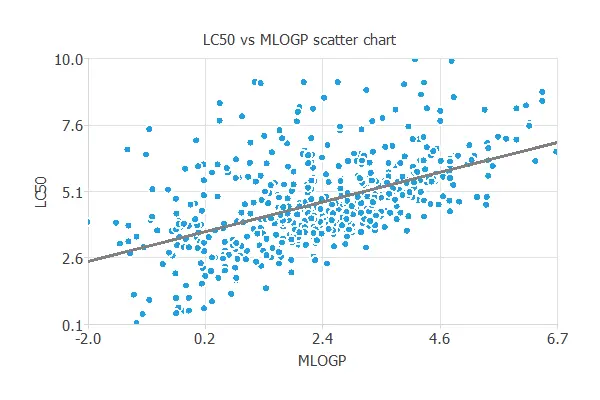
Scatter charts
In a scatter chart, we can visualize how this correlation works.
3. Neural network
The second step is to build a neural network that represents the approximation function.
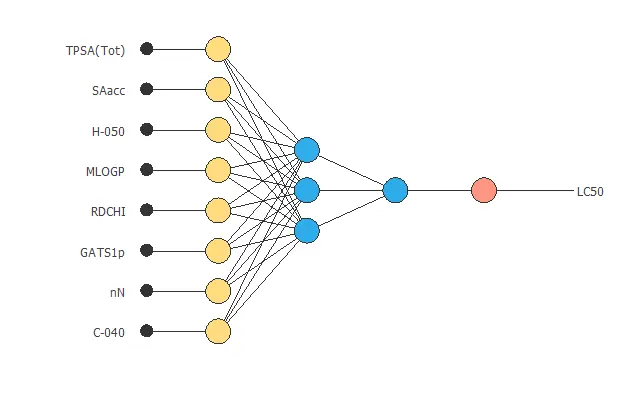
The neural network has 8 inputs (TPSA, SAacc, H-050, MLOGP, RDCHI, GATS1p, nN, C-040) and 1 output (LC50).
It is usually composed of:
- Scaling layer.
- Perceptron layers.
- Unscaling layer.
Scaling layer
The scaling layer contains the statistics of the inputs. We use the automatic setting for this layer to accommodate the best scaling technique for our data.
Dense layers
- The first perceptron layer has 8 inputs, 3 neurons, and a hyperbolic tangent activation function.
- The second perceptron layer has 3 inputs, 1 neuron, and a linear activation function.
Unscaling layer
The unscaling layer contains the statistics of the outputs. We use the automatic method as before.
Neural network graph
The following graph represents the neural network for this example.
4. Training strategy
The fourth step is to select an appropriate training strategy. It is composed of two parameters:
- Loss index.
- Optimization algorithm.
Loss index
The loss index defines what the neural network will learn. It is composed of an error term and a regularization term.
The chosen error term is the normalized squared error, which divides the squared difference between predictions and targets by a normalization factor.
If the normalized squared error has a value of 1, then the neural network predicts the data ‘in the mean,’ while a value of zero means a perfect data prediction.
The regularization used is L2, which limits model complexity by shrinking parameter values.
Optimization algorithm
The optimization algorithm is responsible for searching for the neural network parameters that minimize the loss index.
Here, we chose the quasi-Newton method as an optimization algorithm.
Training
The following chart shows how training error (blue) and validation error (orange) decrease as the number of epochs increases.
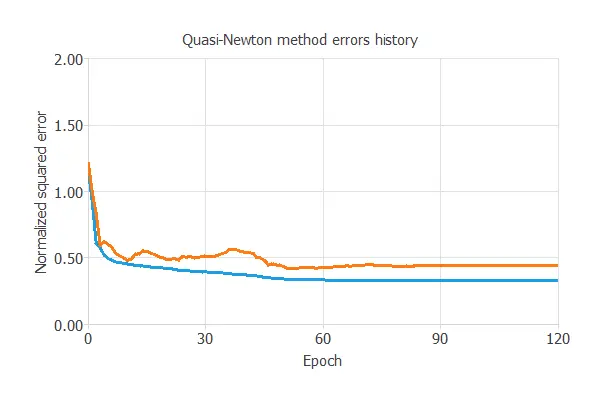
The final values are training error = 0.331 and selection error = 0.481, respectively, in terms of NSE.
Our results are reasonably good, but the model is limited by the small dataset size—a common challenge in machine learning.
5. Testing analysis
The purpose of the testing analysis is to validate the generalization capabilities of the neural network. We use the testing instances in the data set, which have never been used before.
Goodnes-of-fit
A standard testing method in approximation applications is to perform a linear regression analysis between the predicted and the absolute pollutant level values.
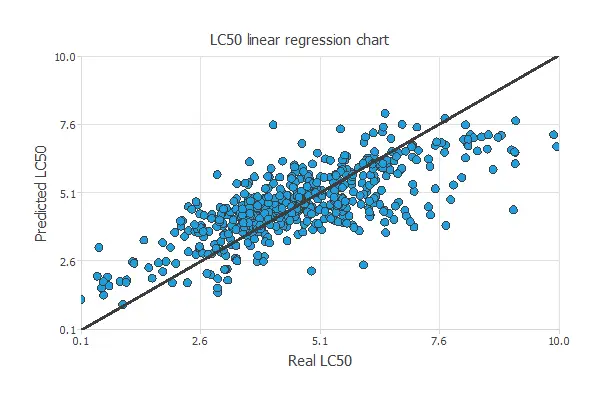
For a perfect fit, the correlation coefficient R2 would be 1. Considering our small dataset issues, we have an R-squared value of 0.744, indicating that the neural network performs well in predicting the testing data.
We have achieved a mean error of 8.64%.
6. Model deployment
In the model deployment phase, the neural network predicts outputs for inputs it has not seen before.
Neural network outputs
We can calculate the neural network outputs for a given set of inputs:
- TPSA(Tot): 48.473.
- SAacc: 58.869.
- H-050: 0.938.
- MLOGP: 2.313.
- RDCHI: 2.492.
- GATS1p: 1.046.
- nN: 1.004.
- C-040: 0.3534.
- LC50: 4.92.
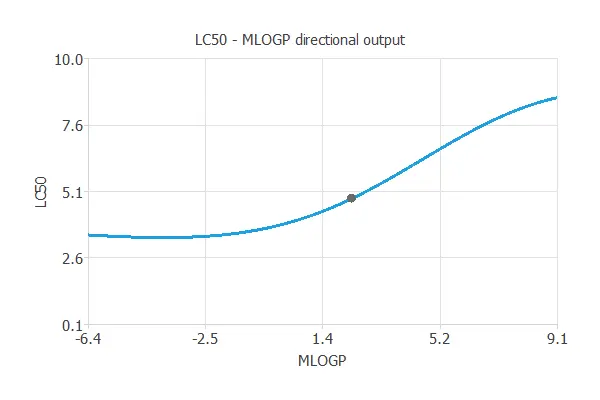
Directional outputs
Directional outputs plot the neural network outputs through some reference points.
The following list shows the reference points for the plots.
- TPSA(Tot): 48.473.
- SAacc: 58.869.
- H-050: 0.938.
- MLOGP: 2.313.
- RDCHI: 2.492.
- GATS1p: 1.046.
- nN: 1.004.
- C-040: 0.3534.
We can see here how MLOGP affects LC50:
References
- M. Cassotti, D. Ballabio, V. Consonni, A. Mauri, I. V. Tetko, R. Todeschini (2014). Prediction of acute aquatic toxicity towards daphnia magna using GA-kNN method, Alternatives to Laboratory Animals (ATLA), 42,31:41.
