This study aims to predict, using machine learning, whether there will be blood donors using a recency, frequency, monetary, and time (RFMT) marketing model.We took the database used for this study from the donor database of Blood Transfusion Service Center in Hsin-Chu City in Taiwan.
Blood donors play a critical role in saving countless lives. However, effectively reaching potential donors can take time and effort.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
1. Application type
The variable to be predicted is binary (donate or not). Therefore, this is a binary classification project.
Using artificial intelligence and machine learning, we aim to model the probability of a person donating blood, conditioned on their features.
2. Data set
Data source
The data file blood_donation.csv contains the information used to create the model. It consists of 748 rows and five columns. The columns represent the variables, and the rows represent the instances.
Variables
The number of input variables, or attributes for each sample, is 5. All input variables are numeric-valued and represent features from blood donors. The target variable is donation, with 0 no blood donation and 1 blood donation for the last campaign. The following list summarizes the variables information:
The next list describes the variables information:
- recency: Months since the last donation.
- frequency: Total number of donations.
- quantity: Total blood donated.
- time: Months since the first donation.
- donation: True if the person donated in the last campaign, false otherwise.
Instances
Finally, the use of all instances is selected. Each patient has an instance that contains the input and target variables. Neural Designer divides the data into three subsets: training, validation, and testing, automatically assigning 60%, 20%, and 20% of the instances for training, generalization, and testing, respectively. The user can modify these values.
Then, we can perform a few related data analyses and check the data has quality.
Variables statistics
We can calculate the data statistics and draw a table with descriptive statistics (minimums, maximums, means, and standard deviations) of all variables in the data set. The next table depicts the values.
| Minimum | Maximum | Mean | Deviation | |
|---|---|---|---|---|
| recency | 0 | 74 | 9.51 | 8.1 |
| frequency | 1 | 50 | 5.51 | 5.84 |
| quantity | 250 | 1.25e+4 | 1.38e+3 | 1.46e+3 |
| time | 2 | 98 | 34.3 | 24.4 |
| donation | 0 | 1 | 0.238 | 0.426 |
Variables distribution
Also, we can calculate the data distributions for each variable. The following pie chart shows the numbers of donations (positives) and no donations (negatives) donors in the data set.
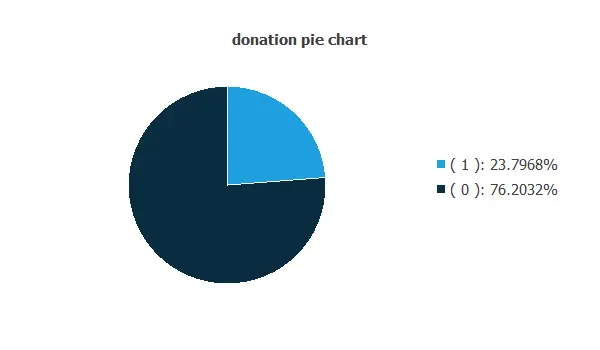
As the image shows, the number of negative responses (i.e., no donations) is much higher than the number of positive responses (76% vs. 23%).
Inputs-targets correlations
The inputs-targets correlations might indicate which factors most influence whether a person would donate blood and, therefore, be more relevant to our analysis.
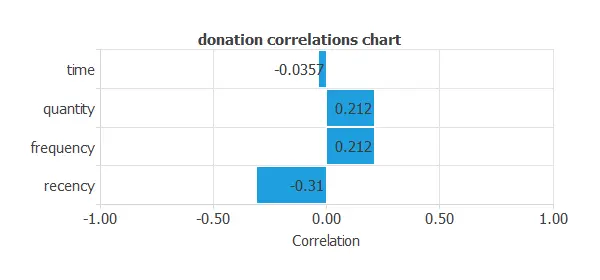
Here, the most correlated variables with blood donation are recency, frequency, and quantity. Also, if we calculate the correlations between the inputs, quantity and frequency correlate 1. So, one can be unused; in this case, we will not use quantity as it has a higher magnitude order.
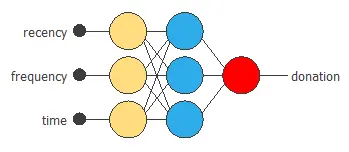
3. Neural network
The next step is to set a neural network representing the classification function. For this type of application, the neural network is composed of:
The scaling layer contains the statistics of the inputs calculated from the data file and the method for scaling the input variables.
Here, the mean and standard deviation scaling method has been set; this scales the inputs to have a mean of 0 and a standard deviation of 1.
We usually apply this method to normal (or Gaussian) distribution variables.
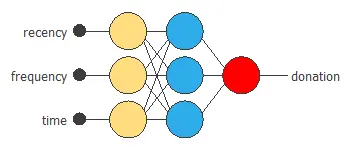
A perceptron layer with a Hyperbolic tangent activation function The neural network needs four inputs since the number of scaling neurons is four. As a starting point, we use three neurons in the hidden layer.
The probabilistic layer contains the method for interpreting the outputs as probabilities. The output of the output layer’s activation function is logistic and interpretable as our target variable’s probability. This probabilistic layer has three inputs, the same as input variables. Its output represents the probability of a person donating blood, conditioned on their features.
The following figure represents the neural network for blood donor prediction.
4. Training strategy
The fourth step is to set the training strategy, which is composed of two terms:
- Loss index.
- An Optimization algorithm.
The loss index chosen is the weighted squared error with L2 regularization.
The learning problem is finding a neural network that minimizes the loss index, or a neural network that fits the data set (error term) and does not oscillate (regularization term).
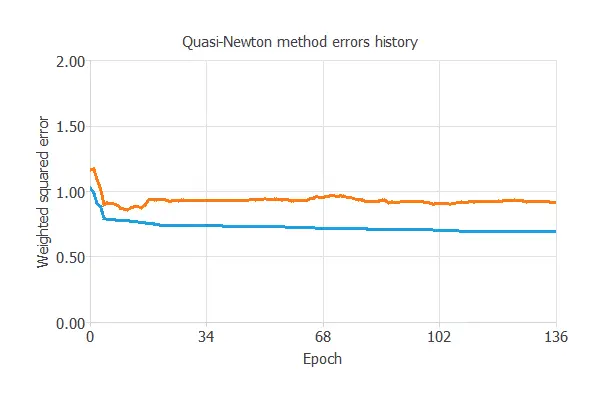
The optimization algorithm that we use is the quasi-Newton method. This is the standard optimization algorithm for this type of problem.
The following chart shows how errors decrease with the iterations during training. The final training and selection errors are training error = 0.778266 WSE and selection error = 0.734308 WSE, respectively.
5. Model selection
The objective of model selection is to find the network architecture that minimizes the error on the selected instances of the data set.
We aim to find a neural network with a selection error lower than 0.734308 WSE, the value we have achieved so far.
Order selection algorithms aim to reduce the selection error by training several network architectures with different numbers of neurons.
The incremental order method increases the number of neurons and their complexity with each iteration. The following graph shows the training error (blue) and selection error (orange) as a function of the number of neurons.
In this case, when we perform a model selection, we slightly improve it, but the model complexity increases too much. Therefore, we opt to maintain our first model as the final model for our study.
6. Testing analysis
The objective of the testing analysis is to validate the performance of the trained neural network. To validate a classification technique, we need to compare the values provided by this technique to the observed values. We can use the ROC curve as it is the standard testing method for binary classification projects.
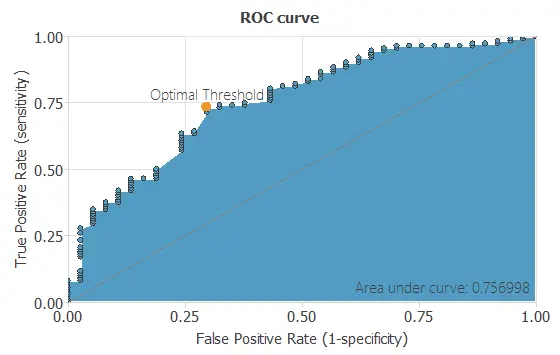
A random classifier has an area under a curve of 0.5. in comparison, the perfect classifier would have an area under a curve of 1. In practice, this measure should take a value between 0.5 and 1. The closer to 1, the better the classifier. In this example, this parameter is AUC = 0.804, which means a great performance.
The following table contains the elements of the confusion matrix. This matrix contains the true positives, false positives, false negatives, and true negatives for the variable diagnosis.
| Predicted negative | Predicted positive | |
|---|---|---|
| Real negative | 72 | 40 |
| Real positive | 10 | 27 |
The binary classification tests are parameters for measuring the performance of a classification problem with two classes:
- Classification accuracy: 66.4% (ratio of correctly classified samples).
- Error rate: 33.6% (ratio of misclassified samples).
- Sensitivity: 64.2% (percentage of actual positive classified as positive).
- Specificity: 73% (percentage of actual negative classified as negative).
7. Model deployment
Once the generalization performance of the neural network has been tested, it can be saved for future use in the so-called model deployment mode.
We can predict whether a person will donate blood by calculating the neural network outputs. For that, we need to set the input variables.
- recency: 9 months since the last donation.
- frequency: 5 number of donations.
- time: 34 months since the first donation.
The predicted donation probability for these values is the following:
- donation: 51% probability.
The objective of the Response Optimization algorithm is to exploit the mathematical model to look for optimal operating conditions. Indeed, the predictive model allows us to simulate different operating scenarios and adjust the control variables to improve efficiency.
An example is to maximize donation probability while maintaining recency between two desired values and remaining inputs below health limits.
The next table resumes the conditions for this problem.
| Variable name | Condition | ||
|---|---|---|---|
| Recency | Between | 4 | 12 |
| Frequency | Less than | 10 | |
| Quantity | Less than | 2000 | |
| Time | Greater than | 4 | |
| Donation probability | Maximize |
The next list shows the optimum values for previous conditions.
- recency: 5 months since the last donation.
- frequency: 9 number of donations.
- frequency: 1582 total donated blood.
- time: 5 months since the first donation.
- donation: 83% probability.
The mathematical expression represented by the neural network is written below. It takes the inputs recency, frequency, monetary, and time to produce the output prediction about donation.
scaled_recency = (recency-9.506679535)/8.095399857; scaled_frequency = (frequency-5.514709949)/5.839310169; scaled_time = (time-34.28210068)/24.37669945; perceptron_layer_1_output_0 = tanh( 0.358944 + (scaled_recency*-0.692014) + (scaled_frequency*-1.37401) + (scaled_time*-0.531336) ); perceptron_layer_1_output_1 = tanh( 0.675304 + (scaled_recency*0.579182) + (scaled_frequency*1.97605) + (scaled_time*-0.334593) ); perceptron_layer_1_output_2 = tanh( -0.501794 + (scaled_recency*-0.801198) + (scaled_frequency*0.234288) + (scaled_time*-0.228785) ); probabilistic_layer_combinations_0 = -0.27896 +0.832439*perceptron_layer_1_output_0 +1.53477*perceptron_layer_1_output_1 +1.72943*perceptron_layer_1_output_2 donation = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);
The above expression can be exported anywhere.
References
-
- The data for this problem has been taken from the UCI Machine Learning Repository.
- Yeh, I-Cheng, Yang, King-Jang, and Ting, Tao-Ming, “Knowledge discovery on RFM model using Bernoulli sequence“, Expert Systems with Applications, 2008.