Diagnose breast cancer from histopathological images using Artificial Intelligence

This example aims to assess whether a lump in a breast could be malignant (cancerous) or benign (non-cancerous). For that, we use digitized histopathological images of fine-needle aspiration (FNA) biopsy using machine learning.

Dr. William H. Wolberg, from the University of Wisconsin Hospitals, Madison, obtained this breast cancer database.

Fine needle aspiration

Contents:

  1. Application type.
  2. Data set.
  3. Neural network.
  4. Training strategy.
  5. Model selection.
  6. Testing analysis.
  7. Model deployment.
  8. Tutorial video.

This example is solved with Neural Designer. To follow it step by step, you can use the free trial.

1. Application type

The variable to be predicted can have two values (malignant or benignant tumor). Therefore, this is a binary classification project.

The goal here is to model the probability of a malignant tumor conditioned on the fine needle aspiration (FNA) test features using artificial intelligence and machine learning.

2. Data set

The breast_cancer.csv file contains the data for this example. Target variables can only have two values in a classification model: 0 (false) or 1 (true). The number of instances (rows) in the data set is 683, and the number of variables (columns) is 10.

The number of input variables, or attributes for each sample, is 9. All input variables are numeric-valued and represent measurements from digitized histopathological images of a fine-needle aspiration (FNA) biopsy. The target variable is 1, diagnose (0 or 1) benign (non-cancerous) or malignant (cancerous), respectively. The following list summarizes the variables information:

Finally, the use of all instances is set. Note that each instance contains the input and target variables of a different patient. The data set is divided into training, validation, and testing subsets. Neural Designer automatically assigns 60% of the instances for training, 20% for generalization, and 20% for testing. The user can choose to modify these values to the desired ones.

Once we have set the data, we can perform a few related analytics. We check the provided information and ensure that the data has good quality.

We can calculate the data statistics and draw a table with descriptive statistics (minimums, maximums, means, and standard deviations) of all variables in the data set. The next table depicts the values.

Minimun Maximun Mean Deviation
clump_thickness 1 10 4.44 2.82
cell_size_uniformity 1 10 3.15 3.07
cell_shape_uniformity 1 10 3.22 2.99
marginal_adhesion 1 10 2.83 2.86
single_epithelial_cell_size 1 10 3.23 2.22
bare_nuclei 1 10 3.54 3.64
bland_chromatin 1 10 3.45 2.45
normal_nucleoli 1 10 2.87 3.05
mitoses 1 10 1.6 1.73
diagnose 0 1 0.35 0.447

All variables are ranked from 1 to 10, with one meaning that the variable for that sample is low, and ten meaning that it is high, e.g., a value of clump_thickness equal to 1 would mean that this sample clump thickness is low. As we can see in the previous table, the mean for all the variables is less than 5. The input variable with the minor standard deviation is "mitoses".

Also, we can calculate the distributions for all variables. The following figure shows a pie chart with the numbers of malignant (positives) and benign (negatives) tumors in the data set.

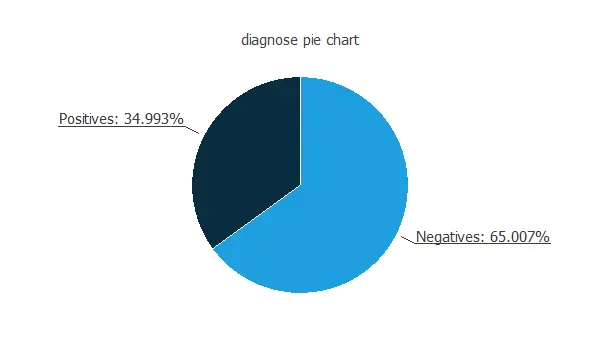
As depicted on the image, malignant tumors represent 35% of the samples, and benign tumors represent approximately 65%.

The inputs-targets correlations might indicate to us which factors most influence whether a tumor is malignant or benign and therefore be more relevant to our analysis.

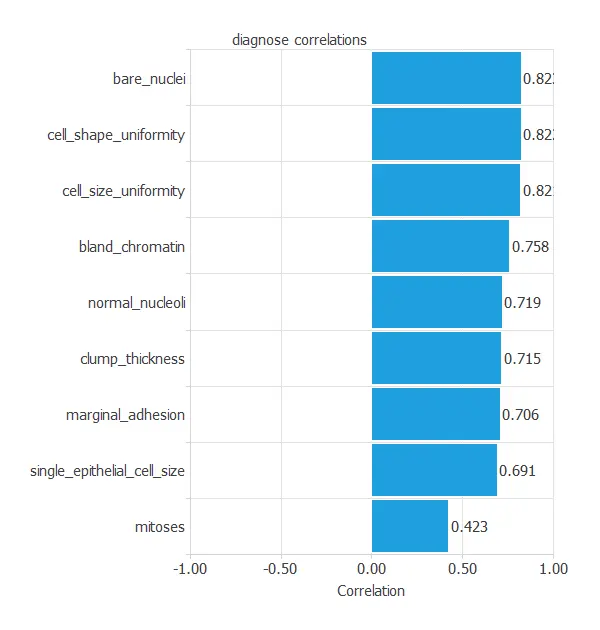
Here, the most correlated variables with malignant tumors are bare nuclei, cell shape uniformity, and cell size uniformity.

3. Neural network

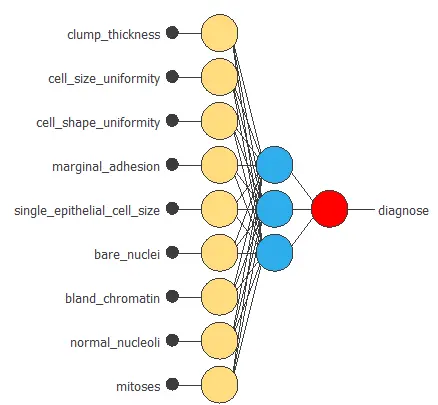
The next step is to set a neural network to represent the classification function. For this class of applications, the neural network is composed of:

The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables. Here the minimum-maximum method has been set. Nevertheless, the mean-standard deviation method would produce very similar results. The scaling layer has nine inputs since there are nine input variables.

A perceptron layer with a hidden logistic layer. The neural network must have nine inputs since the number of scaling neurons is nine. As an initial guess, we use three neurons in the hidden layer.

The probabilistic layer only contains the method for interpreting the outputs as probabilities. Indeed, as the sum of all outputs from a probabilistic layer must be 1, that two methods would always yield one here since there is only one output. Moreover, as the output layer's activation function is the logistic, that output can already be interpreted as a probability of class membership. The probabilistic layer has three inputs. It also has one output, representing the probability of a sample being a malignant tumor.

The following figure is a graphical representation of this neural network for breast cancer diagnosis.

4. Training strategy

The fourth step is to set the training strategy, which is composed of two terms:

The loss index is the weighted squared error with L2 regularization. This is the default loss index for binary classification applications.

We can state the learning problem as finding a neural network that minimizes the loss index. That is, a neural network that fits the data set (error term) and does not oscillate (regularization term).

The optimization algorithm that we use is the quasi-Newton method. This is also the standard optimization algorithm for this type of problem.

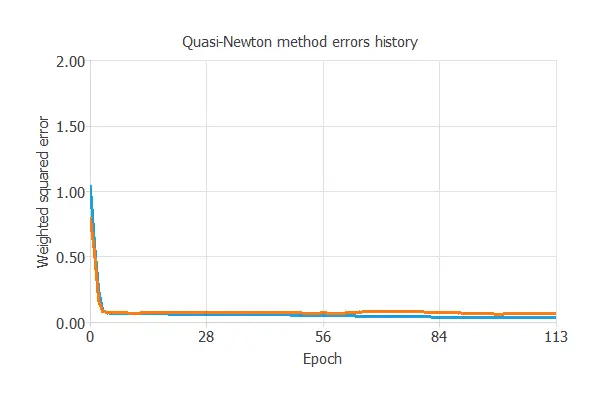
The following chart shows how the error decreases with the iterations during the training process. The final training and selection errors are training error = 0.054 WSE and selection error = 0.072 WSE, respectively.

5. Model selection

The objective of model selection is to find the network architecture with the best generalization properties, that is, that which minimizes the error on the selected instances of the data set.

More specifically, we want to find a neural network with a selection error of less than 0.072 WSE, which is the value that we have achieved so far.

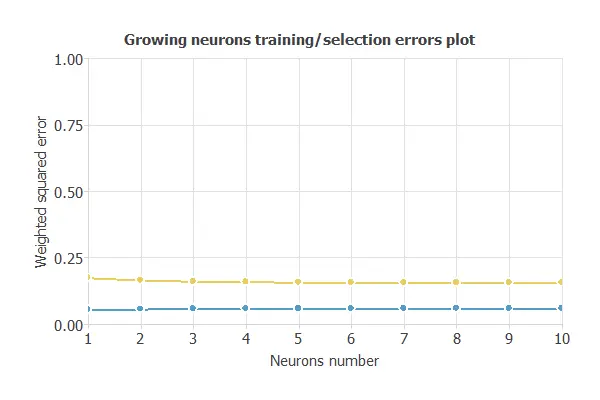
Order selection algorithms train several network architectures with a different number of neurons and select that with the smallest selection error.

The incremental order method starts with a small number of neurons and increases the complexity at each iteration. The following chart shows the training error (blue) and the selection error (orange) as a function of the number of neurons.

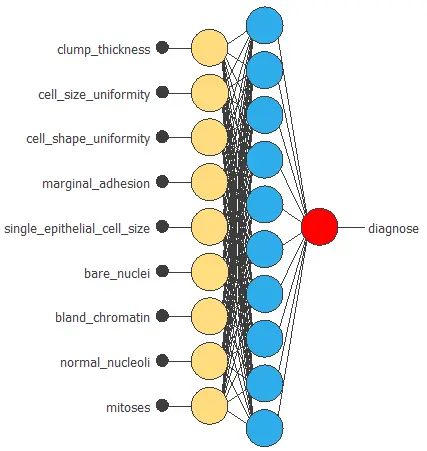
The figure below shows the final architecture for the neural network.

6. Testing analysis

The objective of the testing analysis is to validate the generalization performance of the trained neural network. To validate a classification technique, we need to compare the values provided by this technique to the observed values. We can use the ROC curve as it is the standard testing method for binary classification projects.

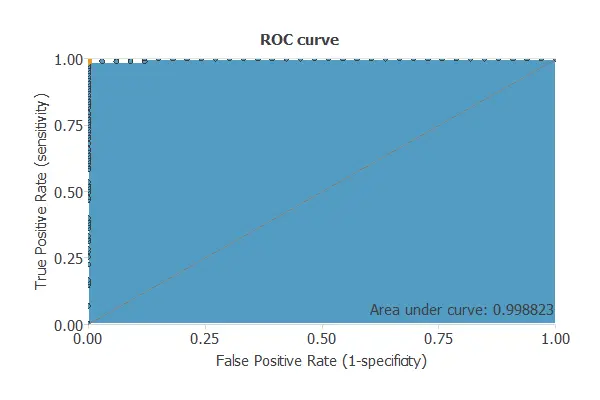
A random classifier has an area under a curve of 0.5, while a perfect classifier has an area under the curve of 1. In practice, this measure should take a value between 0.5 and 1. The closer to 1, the better the classifier. In this example, this parameter is AUC = 0.804, which means a great performance.

The following table contains the elements of the confusion matrix. This matrix contains the true positives, false positives, false negatives, and true negatives for the variable diagnose.

Predicted negative Predicted positive
Real negative 101 2
Real positive 0 33

The binary classification tests are parameters for measuring the performance of a classification problem with two classes:

7. Model deployment

Once the neural network's generalization performance has been tested, the neural network can be saved for future use in the so-called model deployment mode.

We can diagnose new patients by calculating the neural network outputs. For that, we need to know the input variables for them. An example is the following:

The mathematical expression represented by the neural network is written below. It takes the inputs clump_thickness, cell_size_uniformity, cell_shape_uniformity, marginal_adhesion, single_epithelial_cell_size, bare_nuclei, bland_chromatin, normal_nucleoli and mitoses to produce the output diagnose. The information is propagated feed-forward for classification problems through the scaling, perceptron, and probabilistic layers. 

		scaled_clump_thickness = (clump_thickness-4.442170143)/2.818700075;
		scaled_cell_size_uniformity = (cell_size_uniformity-3.150810003)/3.062900066;
		scaled_cell_shape_uniformity = (cell_shape_uniformity-3.215229988)/2.986390114;
		scaled_marginal_adhesion = (marginal_adhesion-2.830159903)/2.862469912;
		scaled_single_epithelial_cell_size = (single_epithelial_cell_size-3.234260082)/2.221460104;
		scaled_bare_nuclei = (bare_nuclei-3.544660091)/3.641190052;
		scaled_bland_chromatin = (bland_chromatin-3.445100069)/2.447900057;
		scaled_normal_nucleoli = (normal_nucleoli-2.869689941)/3.050430059;
		scaled_mitoses = (mitoses-1.603219986)/1.731410027;

		perceptron_layer_1_output_0 = tanh( 0.0344199 + (scaled_clump_thickness*0.181135) + (scaled_cell_size_uniformity*0.217282) + (scaled_cell_shape_uniformity*0.196496) + (scaled_marginal_adhesion*0.125525) + (scaled_single_epithelial_cell_size*-0.0287599) + (scaled_bare_nuclei*0.314836) + (scaled_bland_chromatin*0.0702443) + (scaled_normal_nucleoli*0.18966) + (scaled_mitoses*0.185792) );
		perceptron_layer_1_output_1 = tanh( -0.0365313 + (scaled_clump_thickness*-0.185626) + (scaled_cell_size_uniformity*-0.224576) + (scaled_cell_shape_uniformity*-0.203225) + (scaled_marginal_adhesion*-0.127989) + (scaled_single_epithelial_cell_size*0.029879) + (scaled_bare_nuclei*-0.321838) + (scaled_bland_chromatin*-0.0715547) + (scaled_normal_nucleoli*-0.194488) + (scaled_mitoses*-0.191226) );
		perceptron_layer_1_output_2 = tanh( -0.0362404 + (scaled_clump_thickness*-0.184876) + (scaled_cell_size_uniformity*-0.223219) + (scaled_cell_shape_uniformity*-0.202266) + (scaled_marginal_adhesion*-0.127906) + (scaled_single_epithelial_cell_size*0.0295682) + (scaled_bare_nuclei*-0.321034) + (scaled_bland_chromatin*-0.0711169) + (scaled_normal_nucleoli*-0.193701) + (scaled_mitoses*-0.190348) );
		perceptron_layer_1_output_3 = tanh( -0.0361874 + (scaled_clump_thickness*-0.18509) + (scaled_cell_size_uniformity*-0.223665) + (scaled_cell_shape_uniformity*-0.202517) + (scaled_marginal_adhesion*-0.127643) + (scaled_single_epithelial_cell_size*0.0299014) + (scaled_bare_nuclei*-0.320942) + (scaled_bland_chromatin*-0.0715655) + (scaled_normal_nucleoli*-0.194093) + (scaled_mitoses*-0.190596) );
		perceptron_layer_1_output_4 = tanh( 0.0360132 + (scaled_clump_thickness*0.184484) + (scaled_cell_size_uniformity*0.222643) + (scaled_cell_shape_uniformity*0.201691) + (scaled_marginal_adhesion*0.12739) + (scaled_single_epithelial_cell_size*-0.0299674) + (scaled_bare_nuclei*0.320025) + (scaled_bland_chromatin*0.0714402) + (scaled_normal_nucleoli*0.193439) + (scaled_mitoses*0.189759) );
		perceptron_layer_1_output_5 = tanh( 0.0354705 + (scaled_clump_thickness*0.183133) + (scaled_cell_size_uniformity*0.2203) + (scaled_cell_shape_uniformity*0.199823) + (scaled_marginal_adhesion*0.126653) + (scaled_single_epithelial_cell_size*-0.0295373) + (scaled_bare_nuclei*0.317894) + (scaled_bland_chromatin*0.0708924) + (scaled_normal_nucleoli*0.191821) + (scaled_mitoses*0.188106) );
		perceptron_layer_1_output_6 = tanh( 0.0348187 + (scaled_clump_thickness*0.181724) + (scaled_cell_size_uniformity*0.218308) + (scaled_cell_shape_uniformity*0.197597) + (scaled_marginal_adhesion*0.125867) + (scaled_single_epithelial_cell_size*-0.0290229) + (scaled_bare_nuclei*0.315884) + (scaled_bland_chromatin*0.0705261) + (scaled_normal_nucleoli*0.19041) + (scaled_mitoses*0.186599) );
		perceptron_layer_1_output_7 = tanh( -0.0355217 + (scaled_clump_thickness*-0.183151) + (scaled_cell_size_uniformity*-0.220295) + (scaled_cell_shape_uniformity*-0.199629) + (scaled_marginal_adhesion*-0.126905) + (scaled_single_epithelial_cell_size*0.0293504) + (scaled_bare_nuclei*-0.318226) + (scaled_bland_chromatin*-0.070681) + (scaled_normal_nucleoli*-0.19183) + (scaled_mitoses*-0.188182) );
		perceptron_layer_1_output_8 = tanh( 0.0349867 + (scaled_clump_thickness*0.18201) + (scaled_cell_size_uniformity*0.21809) + (scaled_cell_shape_uniformity*0.197321) + (scaled_marginal_adhesion*0.126417) + (scaled_single_epithelial_cell_size*-0.029256) + (scaled_bare_nuclei*0.316366) + (scaled_bland_chromatin*0.0703615) + (scaled_normal_nucleoli*0.190555) + (scaled_mitoses*0.186607) );
		perceptron_layer_1_output_9 = tanh( 0.0344097 + (scaled_clump_thickness*0.181045) + (scaled_cell_size_uniformity*0.217696) + (scaled_cell_shape_uniformity*0.196321) + (scaled_marginal_adhesion*0.125367) + (scaled_single_epithelial_cell_size*-0.0283902) + (scaled_bare_nuclei*0.314796) + (scaled_bland_chromatin*0.0700932) + (scaled_normal_nucleoli*0.189455) + (scaled_mitoses*0.185805) );

		probabilistic_layer_combinations_0 = -0.0355815 +0.58858*perceptron_layer_1_output_0 -0.605611*perceptron_layer_1_output_1 -0.603077*perceptron_layer_1_output_2 -0.603653*perceptron_layer_1_output_3 +0.601335*perceptron_layer_1_output_4 +0.596165*perceptron_layer_1_output_5 +0.591153*perceptron_layer_1_output_6 -0.596392*perceptron_layer_1_output_7 +0.59155*perceptron_layer_1_output_8 +0.588449*perceptron_layer_1_output_9 
			
		diagnose = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);

The above expression can be exported anywhere, for instance, to a dedicated diagnosis software used by doctors.

8. Tutorial video

You can watch the step by step tutorial video below to help you complete this Machine Learning example for free using the easy-to-use machine learning software Neural Designer.

References:

Related posts: