They want to understand the factors affecting the pricing of cars in the American market. Indeed, those may be very different from the Chinese market. Additionally, the company wants to know which variables are significant in predicting the price of a car and how well those variables describe the price based on various market surveys.
Performance optimization can be applied to understand the behavior of the American car market.
For this study, we have gathered a large data set of different types of cars across the American market.
We are required to model the price of cars with the available independent variables. The company management will use it to understand how the prices vary with the independent variables. Consequently, they can accordingly manipulate the design of the cars, the business strategy, etc., to meet certain price levels. Further, the model will be a good way for management to understand the pricing dynamics of a new market.
Contents
This example is solved with Neural Designer. To follow it step by step, you can use the free trial.
1. Application type
This is an approximation project since the variable to be predicted is continuous (car price).
The fundamental goal here is to model the pricing of cars as a function of several car features and different types of engines.
2. Data set
The first step is to prepare the data set, which is the source of information for the approximation problem. It is composed of:
- Data source.
- Variables.
- Instances.
Data source
The file car_price_assignment.csv contains the data for this example. Here the number of variables (columns) is 26, and the number of instances (rows) is 205.
Variables
In that way, this problem has the 25 following variables:
- car_id, unique ID of each observation.
- symboling, it is an insurance risk rating; a value of +3 indicates that the auto is risky, and -3 indicates that it is probably pretty safe.
- car_brand, brand of the car company.
- car_name, specific model of the car.
- fuel_type, car fuel type i.e., gas or diesel.
- aspiration, aspiration used in a car; “std” for standard and “turbo”.
- door_number, number of doors in a car.
- car_body, the body of a car could be: hardtop, wagon, sedan, hatchback and convertible.
- drive_wheel, type of drivewheel;”fwd” stands for front wheel drive, “4wd” stands for four wheel drive and “rwd” stands for rear wheel drive.
- engine_location, rear or front location of the car engine.
- wheel_base, is the distance between the front and rear wheels, in Inches.
- car_length, in Inches.
- car_width, in Inches.
- car_height, in Inches.
- curb_weight, weight of a car without occupants or baggage, in Libras.
- engine_type, “ohc” stands for Overhead Camshaft engines, “ohcv” stands for Overhead Valve engines, “ohc” stands for Overhead Camshaft engines, “ohcf”,”dohc” stands for Dual Overhead Camshaft engines, “l” for L engines, “dohcv” stands for Dual Overhead Valve engines and “rotor” .
- cylinder_number, number of cylinders.
- engine_size, in Cubic Centimetres.
- fuel_system, “mpfi” stands for Multi Point Fuel injection, “1ppl”, “2bbl”, “4bbl”, “idi”, “mfi”, “spdi”, “spfi”.
- bore_ratio, adimensional quantity calculated by the ratio between cylinder bore diameter and piston stroke length.
- stroke, the distance traveled by the piston during each cycle, in inches.
- compression_ratio, adimensional quantity calculated by the ratio between the volume of the cylinder and combustion chamber when the piston is at the bottom of its stroke, and the volume of the combustion chamber when the piston is at the top of its stroke.
- horse_power, in HorsePower.
- peak_rpm, in revolutions per minute.
- city_mpg, it shows how far your car can travel in the city for every gallon of gas, in miles per gallon.
- highway_mpg, it shows how far your car can travel on the highway for every gallon of gas, in miles per gallon.
- price, the final price in Dollars.
All the variables in the study are inputs, except for ‘fuel_system’, ‘car_brand’ and ‘car_name’ which are set to stay as “unused”, and ‘price’, which is the output we want to extract from this machine learning study.
Moreover, we realize that Neural Designer left the first variable, ‘car_id’, out of the total number of variables because it does not have a useful value to this study.
They are divided randomly into training, selection, and testing subsets, containing 60%, 20%, and 20% of the instances, respectively. More specifically, 123 samples are used here for training, 41 for validation, and 41 for testing.
Data distribution
Once all the data set information has been set, we will perform some analytics to check the quality of the data.
For instance, we can calculate the data distribution. The next figure depicts the histogram for the target variable.
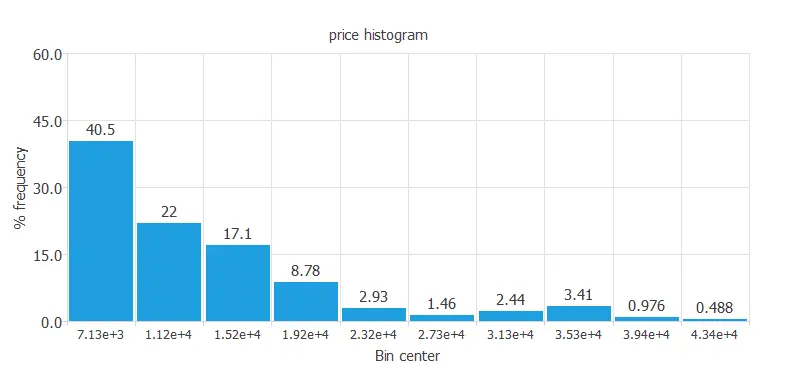
As we can see in the diagram, the car price has a normal distribution because we expect American customers to buy cars at a low-medium range of prices. However, only a few percent of the American population can buy expensive cars, as the median personal income of Americans is not extremely high.
Inputs-targets correlations
The next figure depicts inputs-targets correlations. This might help us see the different inputs’ influence on the final price.
We realized that certain instances correlate very poorly with our final target. Therefore, to show more conclusive results, we can exclude some of the study variables by clicking on ‘Unuse uncorrelated variables’ on the Task Manager window, and inserting a minimum correlation value of 0.01 (the lower value we can write), for example.
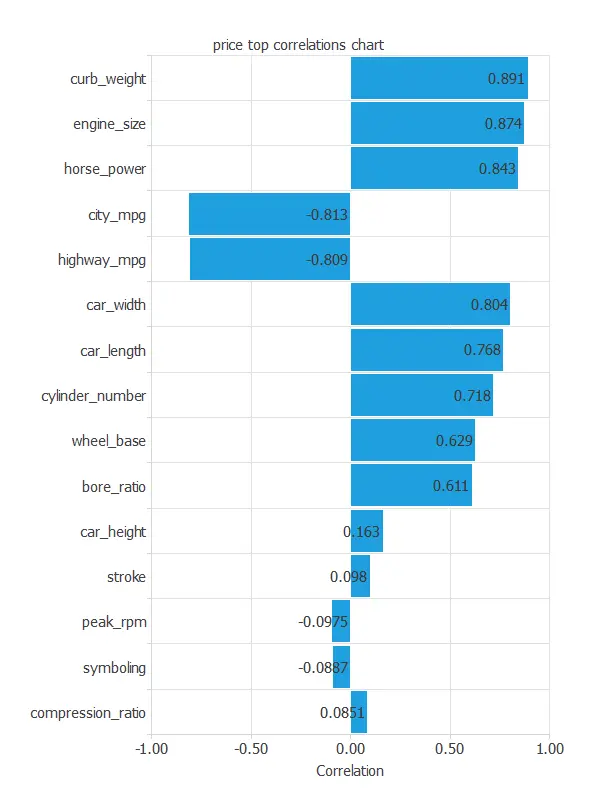
The above chart shows that a few instances have an important dependency on the car price. As we can see, curb weight, engine size, and horsepower positively affect the price; the bigger the engine size, the more expensive the car is. On the other hand, some instances (city and highway miles per gallon consumption) have an important negative dependency on the price. The less the car consumes, the higher the price is.
We can also plot a scatter chart with the price versus the horsepower.
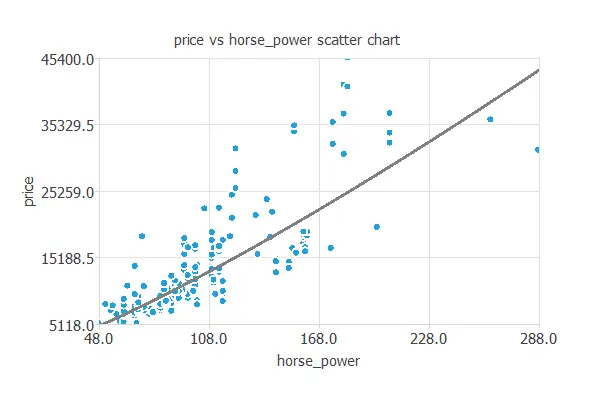
In general, the more horsepower, the higher the price. However, the price depends on all the inputs at the same time.
3. Neural network
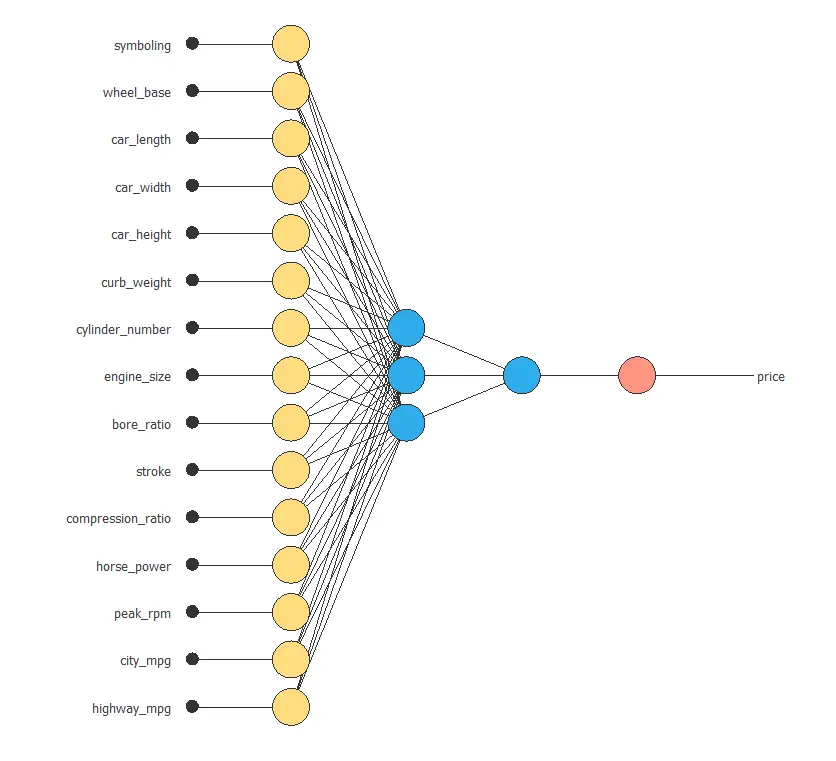
The neural network will output the closing price as a function of all the different car features shown previously.
For this approximation example, the neural network is composed of:
- Scaling layer.
- Perceptron layers.
- Unscaling layer.
The scaling layer transforms the original inputs to normalized values. In this case, we set a mean and standard deviation scaling method so that the input values have a mean of 0 and a standard deviation of 1.
Following this, two perceptron layers are added to the neural network. This number of layers is enough for most applications. The first layer has 15 inputs and 3 neurons, while the second layer consists of 3 inputs and 1 neuron.
The unscaling layer transforms the normalized values from the neural network into the original outputs. In this instance, the mean and standard deviation unscaling method will also be used.
The next figure shows the resulting network architecture.
4. Training strategy
The next step is selecting an appropriate training strategy to define what the neural network will learn. A general training strategy is composed of two concepts:
- A loss index.
- An optimization algorithm.
The loss index chosen is the normalized squared error with L1 regularization. Although the default loss index for approximation problems includes L2 regularization, we obtain a lower selection error with L1 regularization in this case.
The optimization algorithm chosen is the quasi-Newton method. This optimization algorithm is the default for medium-sized applications like this one.
Once we have set the strategy, we can train the neural network. The following chart shows how the training (blue) and selection (orange) errors decrease with the training epoch during the training process.
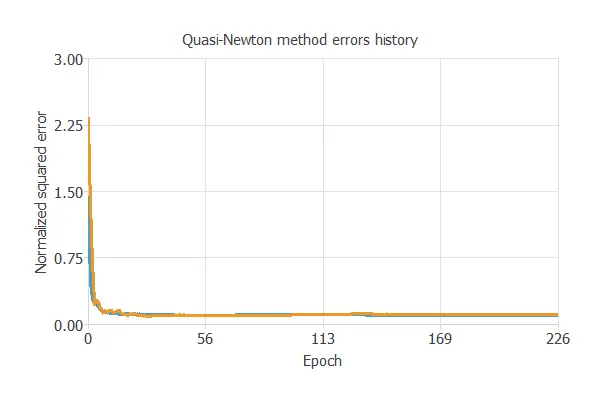
The most important training result is the final selection error. Indeed, this is a measure of the generalization capabilities of the neural network. Here, the final selection error is Selection error = 0.109 NSE.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties. We want to improve the final selection error obtained before (0.209 NSE).
The best selection error is achieved using a model whose complexity is the most appropriate to produce an adequate data fit. Consequently, order selection algorithms are responsible for finding the optimal number of perceptrons in the neural network.
As we can see, the final training error always decreases with the number of neurons. However, the final selection error takes a minimum value at some point. Here, the optimal number of neurons is 8, corresponding to a 0.0974 selection error.
The following figure shows the optimal network architecture for this application.
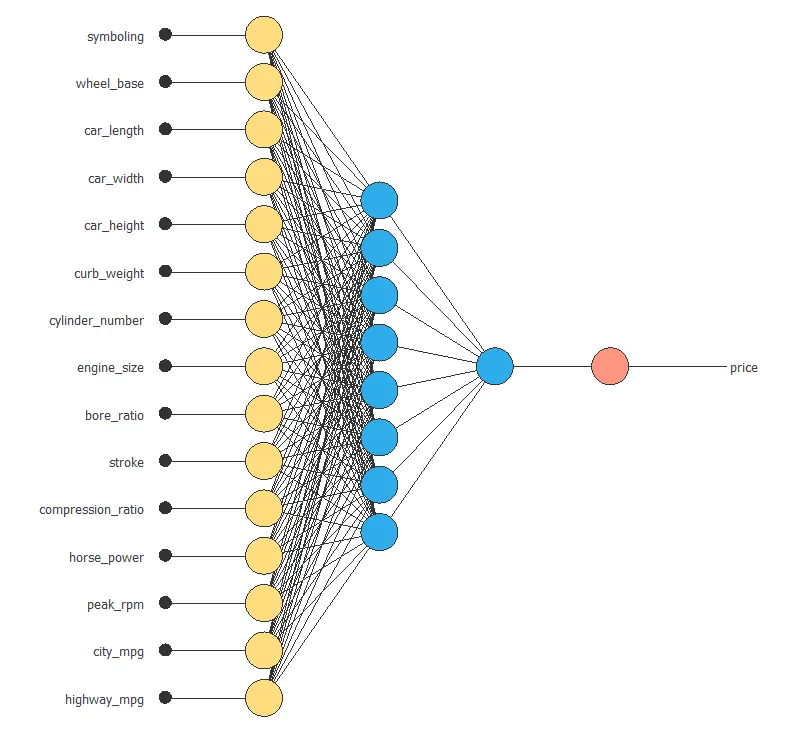
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network. During this process, the testing phase involves comparing the values provided by this technique to the observed values.
A standard testing technique in approximation problems is to perform a linear regression analysis between the predicted and the real values using an independent testing set. The next figure illustrates a graphical output provided by this testing analysis.
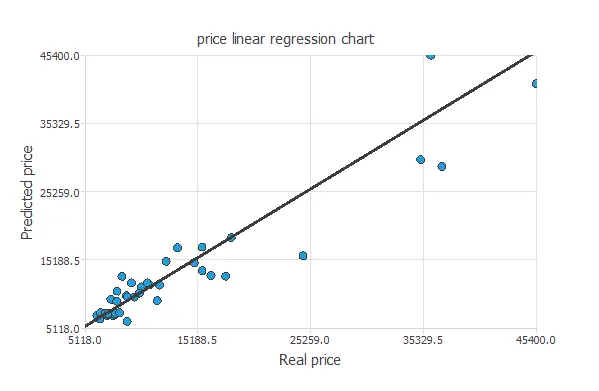
From the above chart, we can see that the neural network is predicting the entire range of car price data well. The correlation value is R2 = 0.937, indicating the model has a reliable prediction capability.
7. Model deployment
The model is now ready to estimate the price of a certain car with satisfactory quality over the same data range.
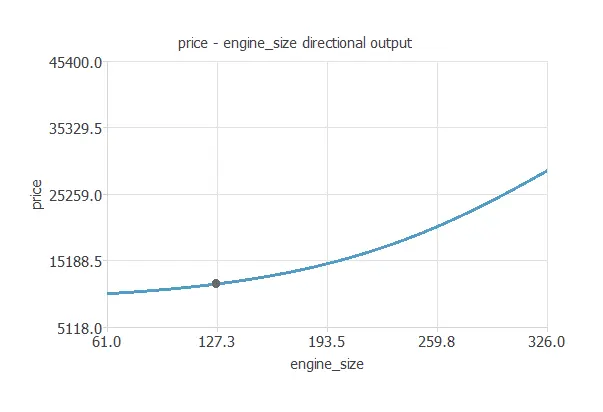
We can plot a directional output of the neural network to see how the price varies with a given input for all other inputs fixed. The next plot shows the car price as a function of the engine size through the following point:
- symboling: 2
- fuel_type: “Diesel”.
- aspiration: “turbo”.
- drive_wheel: “rwd”.
- wheel_base: 98.8 in.
- car_length: 174 in.
- car_width: 65.9 in.
- car_height: 53.7 in.
- curb_weight: 2560 lb.
- engine_type: “dohc”.
- cylinder_number: 4.
- engine_size: 127 cc.
- bore_ratio: 3.33.
- stroke: 3.26 in.
- compression_ratio: 10.1.
- horse_power: 104 hp.
- peak_rpm: 5130 rpm.
- city_mpg: 25.2 mpg.
- highway_mpg: 30.8 mpg.
The car_price.py contains the Python code for the car price.
References
- Kaggle Machine Learning Repository. Car Price Assignment Data Set.


