This example shows how machine learning can create a digital twin of an electric motor.

With the rise of electric vehicles, companies need engines that deliver reliability, autonomy, and durability.

To achieve this, they run digital tests that prevent damage to real motors and help identify the best temperature ranges for performance.

In this study, we use a large dataset of sensor readings from a permanent magnet synchronous motor tested on a bench.

By estimating rotor and stator temperatures, the automotive industry can cut power losses, control heat, and enhance motor design.

We have built this model using the data science and machine learning platform Neural Designer.

You can use the free trial to follow this example step by step.

Contents

  1. Application type.
  2. Data set.
  3. Neural network.
  4. Training strategy.
  5. Model selection.
  6. Testing analysis.
  7. Model deployment.

1. Application type

This is an approximation project since the variable to be predicted is continuous (engine temperature).

The main goal is to understand how voltage and current influence car performance and motor temperature.

2. Data set

The first step is to prepare the data set, which is the source of information for the approximation problem. It is composed of:

  • Data source.
  • Variables.
  • Instances.

Data source

The file permanent_magnet_synchronous_motor.csv contains the data for this example.

Here, the number of variables (columns) is 14, and the number of instances (rows) is 107.

Variables

In that way, this problem has the following variables:

Environmental variables

  • temperature_ambient – Ambient temperature measured near the stator.

Electrical variables

  • voltage_direct – Voltage d-component.
  • voltage_quadrature – Voltage q-component.
  • current_direct – Current d-component.
  • current_quadrature – Current q-component.
  • voltage_module – Voltage vector module from d-q components.
  • current_module – Current vector module from d-q components.

Performance variables

  • speed_motor – Motor speed.
  • torque – Torque induced by current (sometimes used as a target variable).

Thermal variables

  • temperature_coolant – Coolant outflow temperature (water-cooled motor).
  • temperature_stator_yoke – Stator yoke temperature (thermal sensor).
  • temperature_stator_tooth – Stator tooth temperature (thermal sensor).
  • temperature_stator_winding – Stator winding temperature (thermal sensor).

In this study, we use several environmental, electrical, and current variables as inputs to predict motor performance and internal temperatures.

The goal is to model motor behavior and prevent overheating.

Instances

The data is randomly split into 60% training (65 samples), 20% selection (21 samples), and 20% testing (21 samples).

Variables distribution

Once we establish the data set information, we perform analytics to check the data quality.

For instance, we can calculate the data distribution. The following figure depicts the histogram for one of the target variables.

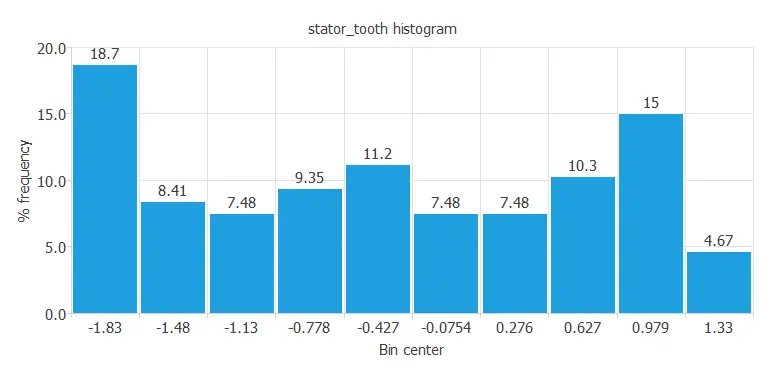
This diagram shows a normal distribution of the stator tooth temperature, one of the stator components.

The distribution appears normal because the output depends on many input variables, which vary constantly during the experiment.

Inputs-targets correlations

The following figure depicts input-target correlations. This might help us see the different inputs’ influence on the motor temperature.

As this machine learning study has various target variables, we show the correlation diagram of one.

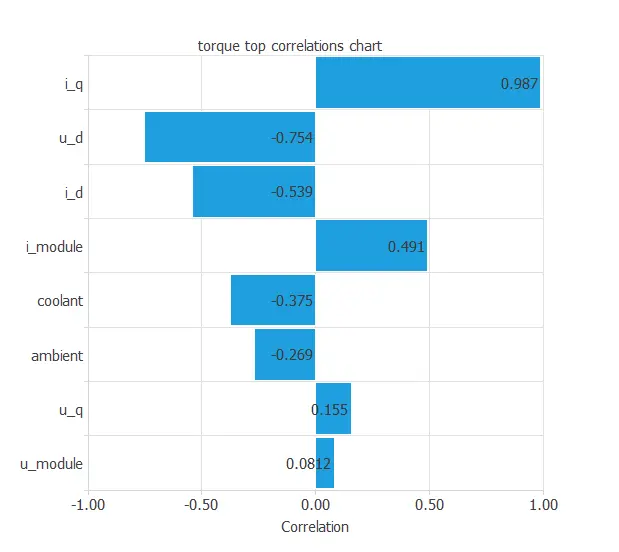
The above chart shows that a few instances have a critical dependency on the variable ‘torque’. As we can see, an instance is highly correlated to this target, as seen in the input ‘current_quadrature’.

At first sight, we could have predicted this behavior simply by looking at the data set and realizing the torque is induced by the current, in this case, by the quadrature coordinate of the current.

Scatter charts

We can also plot a scatter chart with the stator winding temperature versus the ambient temperature.

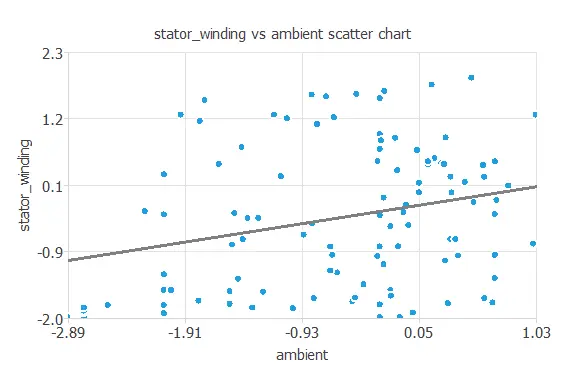
Logically, the higher the ambient temperature, the higher the stator winding temperature.

3. Neural network

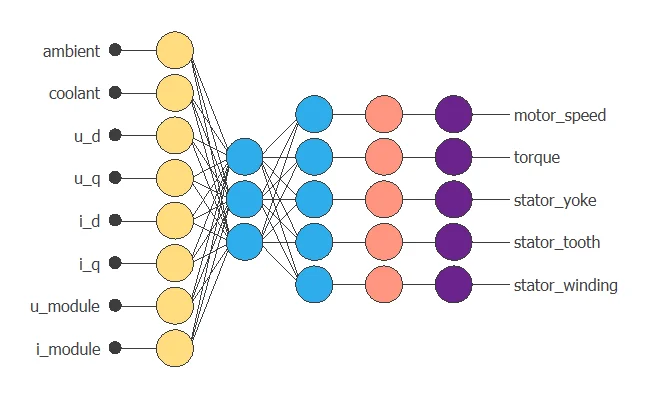
The neural network outputs the different motor temperatures as a function of the current, voltage, coolant, and ambient temperature.

Approximation models usually contain the following layers:

  • Scaling layer.
  • Perceptron layers.
  • Unscaling layer.

Scaling layer

The scaling layer transforms the original inputs to normalized values.

Here, we set the mean and standard deviation scaling method so that the input values have a mean of 0 and a standard deviation of 1.

Dense layers

Here, two perceptron layers are added to the neural network. This number of layers is enough for most applications. The first layer has eight inputs and three neurons. The second layer has three inputs and five neurons.

Unscaling layer

The unscaling layer transforms the normalized values from the neural network into the original outputs.

Here, we also use the mean and standard deviation unscaling method.

The following figure shows the resulting network architecture.

4. Training strategy

The next step is to select an appropriate training strategy that defines what the neural network will learn. A general training strategy is composed of two concepts:

  • A loss index.
  • An optimization algorithm.

The loss index chosen is the normalized squared error with L2 regularization. This loss index is the default in approximation applications.

The optimization algorithm chosen is the quasi-Newton method. This optimization algorithm is the default for medium-sized applications like this one.

Once the strategy has been set, we can train the neural network.

The following chart shows how the training (blue) and selection (orange) errors decrease with the training epoch during the training process.

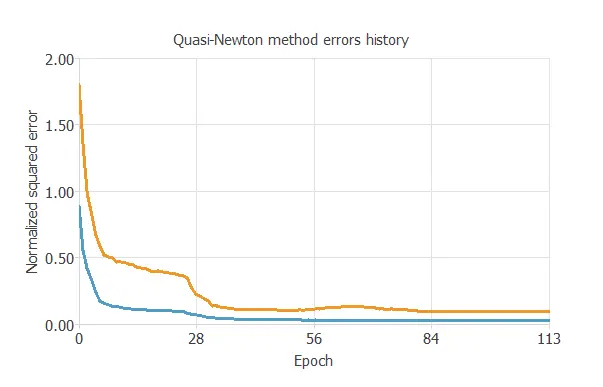
The key training result is the final selection error, which measures the neural network’s generalization ability.

In this case, the final selection error is 0.083 NSE.

5. Model selection

The objective of model selection is to find the network architecture with the best generalization properties. We want to improve the final selection error obtained before (0.083 NSE).

The best selection error is achieved using a model whose complexity is the most appropriate to produce a good data fit. Order selection algorithms are responsible for finding the optimal number of perceptrons in the neural network.

The final training error continuously decreases with the number of neurons. However, the final selection error takes a minimum value at some point. Here, the optimal number of neurons is 9, corresponding to a selection error of 0.043.

The following figure shows the optimal network architecture for this application.

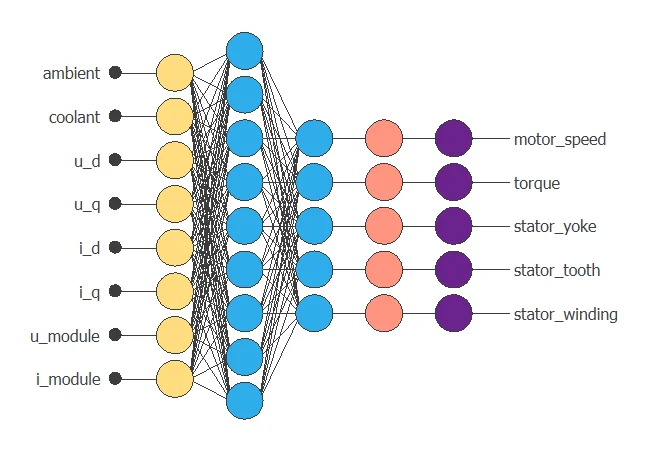
6. Testing analysis

The objective of the testing analysis is to validate the generalization performance of the trained neural network. The testing compares the values provided by this technique to the observed values.

A standard testing technique in approximation problems is to perform a linear regression analysis between the predicted and the real values using an independent testing set. The following figure illustrates a graphical output provided by this testing analysis.

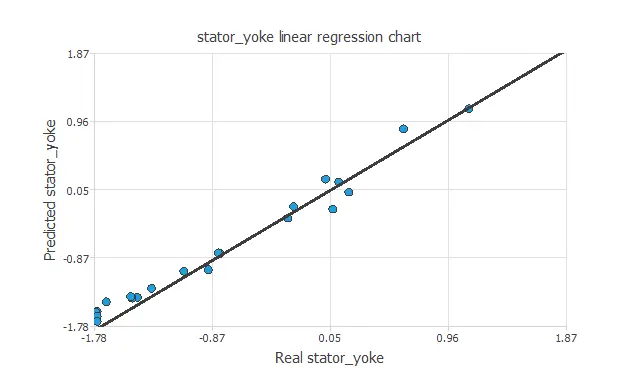
The above chart shows that the neural network is predicting the entire range of temperature data well. The correlation value is R2 = 0.990, indicating the model has a reliable prediction capability.

7. Model deployment

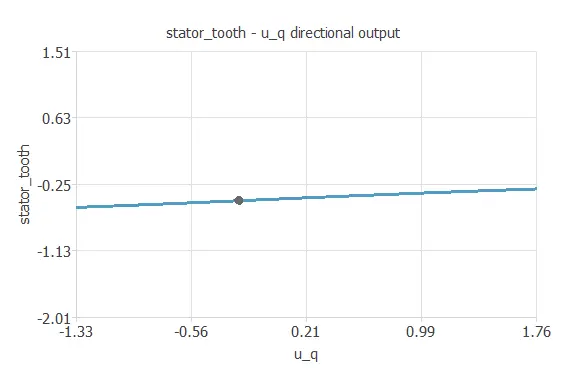
We can plot a directional output of the neural network to see how the targets vary with a given input for all other fixed inputs.
The next plot shows the stator tooth temperature as a function of the quadrature coordinate of the voltage through the following points:

  • temperature_ambient: -0.603. (scaled: Mean=0, Deviation=1)
  • temperature_coolant: -0.393. (scaled: Mean=0, Deviation=1)
  • voltage_direct: -0.359. (scaled: Mean=0, Deviation=1)
  • voltage_quadrature: -0.235. (scaled: Mean=0, Deviation=1)
  • current_direct: 0.0834. (scaled: Mean=0, Deviation=1)
  • current_quadrature: 0.231. (scaled: Mean=0, Deviation=1)
  • voltage_module: 1.26. (scaled: Mean=0, Deviation=1)
  • current_module: 1.19. (scaled: Mean=0, Deviation=1)

The electric_motor.py contains the Python code for the electric motor temperature Neural Network.

References

Related posts

4 machine learning examples in the automotive industry Inspect milk quality using machine learning Predict airfoil self-noise using machine learning Air compressor predictive maintenance using machine learning