Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
This example is solved with Neural Designer. We recommend you follow it step by step using the free trial.
1. Application type
The predicted variable can have three values corresponding to a penguin species: Adelie, Gentoo, and Chinstrap. Therefore, this is a multiple classification project.
To model the probability of each sample belonging to a penguin species is the goal of this example.
2. Data set
Data source
The penguin_dataset.csv file contains the data for this example. Target variables have three values in our classification model: Adelie (0), Gentoo (1), and Chinstrap (2). The number of rows (instances) in the data set is 334, and the number of variables (columns) is 11.
Variables
The number of input variables, or attributes for each sample, is 9. The target variable is 1, species (adelie, gentoo, and chinstrap). The following list summarizes the variables information:
- clutch_completion: a character string denoting if the study nest observed with a full clutch, i.e., 2 eggs.
- date_egg: a date denoting the date study nest observed with 1 egg (sampled).
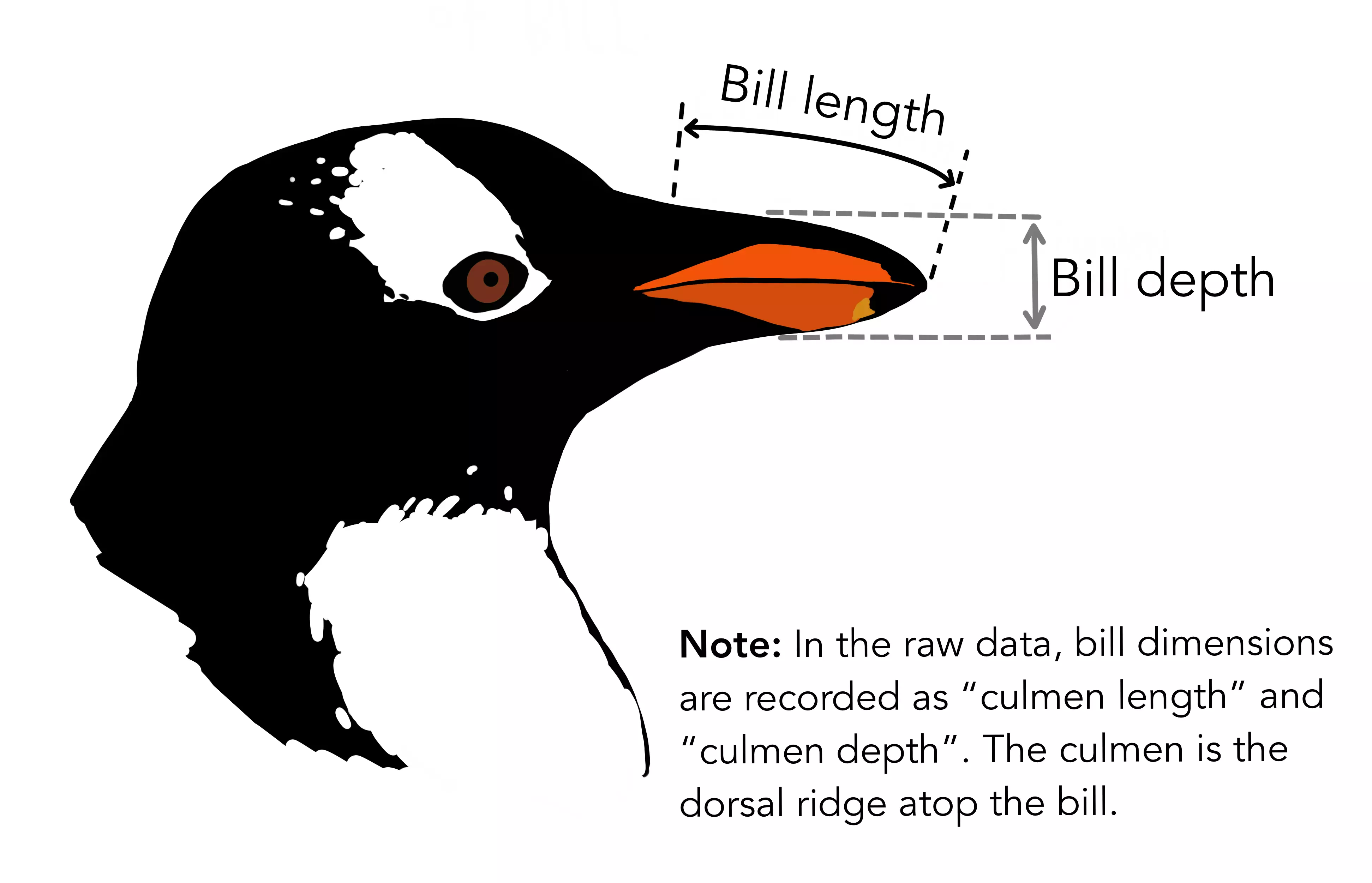
- culmen_length_mm: a number denoting the length of the dorsal ridge of a bird’s bill (millimeters).
- culmen_depth_mm: a number denoting the depth of the dorsal ridge of a bird’s bill (millimeters).
- flipper_length_mm: an integer denoting the length penguin flipper (millimeters).
- body_mass_g: an integer denoting the penguin’s body mass (grams).
- sex: a factor denoting penguin sex (female, male).
- delta_15_N: a number denoting the measure of the ratio of stable isotopes 15N:14N.
- delta_13_C: a number denoting the measure of the ratio of stable isotopes 13C:12C.
Instances
To start, we use all instances. Each row contains the input and target variables of a different sample. The data set is subdivided into training, validation, and testing. Neural Designer automatically assigns 60% of the samples for training, 20% for selection, and 20% for testing. These values can be modified by the user to the desired ones.
Variables distributions
Also, we can calculate the distributions of all variables. The following pie chart shows how many species we have.
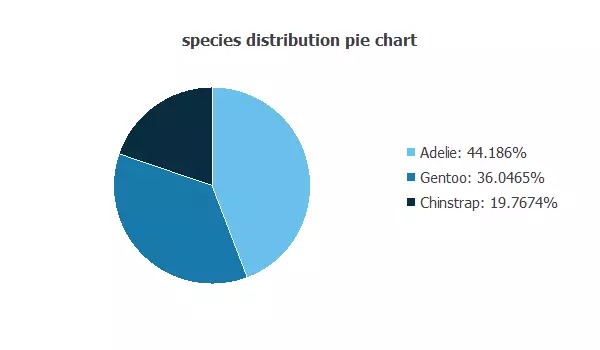
The image shows the proportion of each penguin species: Adelie (44.18%), Gentoo (36,04%), and Chinstrap (19.76%).
Inputs-targets correlations
The inputs-targets correlations might indicate which factors most differentiate between penguins and, therefore, be more relevant to our analysis.
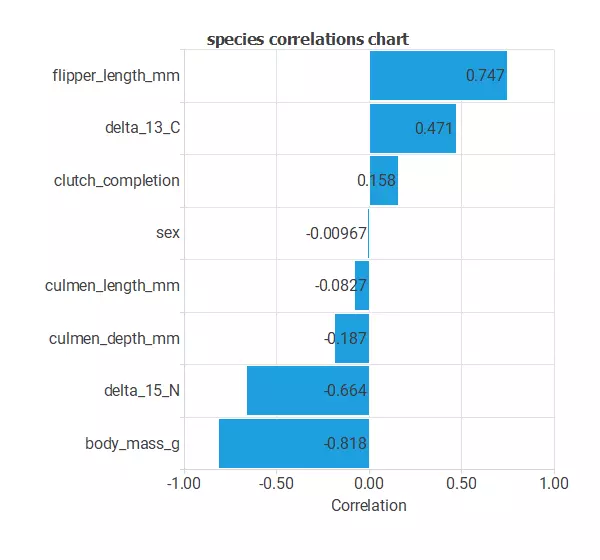
Here, the most correlated variables with penguin species are date_egg, culmen_depth_mm, delta_13_C and delta_15_N.
3. Neural network
The next step is to set a neural network as the classification function. Usually, the neural network is composed of:
The scaling layer contains the inputs scaled from the data file and the method for doing so. Here, the method selected is the minimum-maximum. As we use ten input variables, the scaling layer has ten inputs.
The perceptron layer has 3 neurons with 9 outputs for each neuron.
The probabilistic layer contains the method for interpreting the outputs of the inner layers as probabilities. The output layer’s activation function is the Softmax, so the output can be interpreted as a probability of class membership. The probabilistic layer has ten inputs. It has three outputs, representing the probability of a sample belonging to a class.
The following figure represents the neural network:
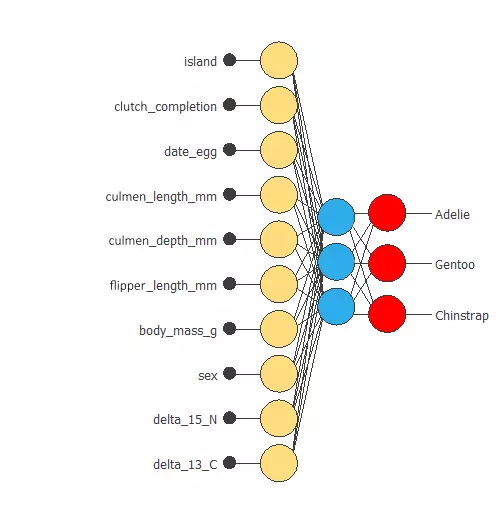
The network has ten inputs, obtaining three output values as mentioned above. These values are the probability of class membership for each patient.
4. Training strategy
The fourth step is to set the training strategy, which is composed of two terms:
- A loss index.
- An optimization algorithm.
The loss index is the normalized squared error with L2 regularization, the default loss index for classification applications.
The aim is to find a neural network that minimizes the error or a neural network that fits the data set (error term) and does not oscillate (regularization term).
The optimization algorithm we use is the quasi-Newton method, the standard optimization algorithm for this type of problem.
The following image shows how the error decreases with the iterations during the training process. The final training and selection errors are training error = 0.004 and selection error = 0.005, respectively.
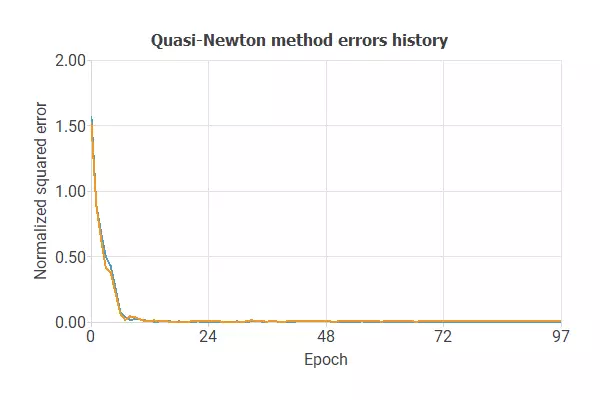
The curves have converged, as we can see in the previous image. However, the selection error is a bit higher than the training error.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties for the data.
Order selection algorithms train several network architectures with different numbers of neurons. Then, it chooses the one with the smallest selection error.
However, we will use input selection to select features in the data set that provide the best generalization capabilities.
As we see in the following image, we reduce the selection error by increasing a bit the training error, thus improving our model.
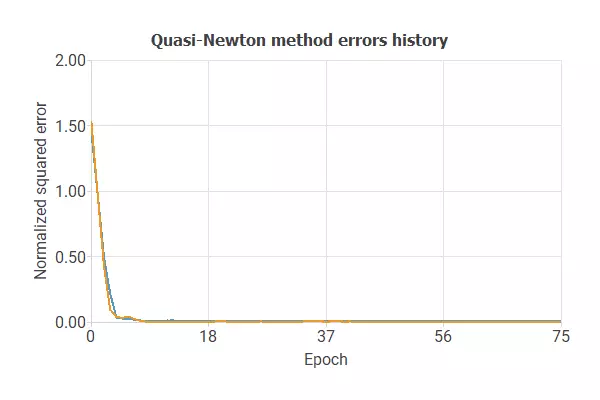
Ultimately, we obtain a training error = 0.01 and a selection error = 0.003. Also, we have reduced the inputs to four. Our network is now like this:
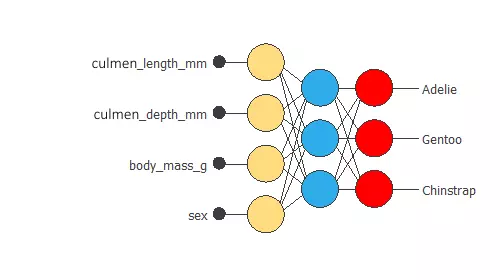
Our final network has 4 inputs corresponding to culmen_length_mm, culmen_depth_mm, body_mass_g, and sex.
6. Testing analysis
The objective of the testing analysis is to validate the generalization properties of the trained neural network. The method to validate the performance of our model is to compare the predicted values to the real values, using a confusion matrix. The next table contains the values of the confusion matrix. The rows represent the real classes in the confusion matrix, and the columns are the predicted classes for the testing data.
| Predicted Adelie | Predicted Gentoo | Predicted Chinstrap | |
|---|---|---|---|
| Real Adelie | 22 (32.353%) | 0 | 1 (1.471%) |
| Real Gentoo | 0 | 31 (45.588%) | 1 (1.471%) |
| Real Chinstrap | 0 | 0 | 13 (19.118%) |
As we can see, we can classify 66 (97.1%) of the samples, while we fail to do so for 2 (2.9%) samples
7. Model deployment
Once we have tested the neural network’s performance, we can save it for the future using the model deployment mode.
The mathematical expression represented by the neural network is written below.
scaled_culmen_length_mm = (culmen_length_mm-43.9219017)/5.443640232; scaled_culmen_depth_mm = (culmen_depth_mm-17.15119934)/1.969030023; scaled_body_mass_g = (body_mass_g-4201.75)/799.6129761; scaled_sex = sex*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; perceptron_layer_1_output_0 = tanh( -0.246009 + (scaled_culmen_length_mm*-2.33036) + (scaled_culmen_depth_mm*1.0486) + (scaled_body_mass_g*0.333745) + (scaled_sex*0.50902) ); perceptron_layer_1_output_1 = tanh( 0.158568 + (scaled_culmen_length_mm*0.0934119) + (scaled_culmen_depth_mm*0.819869) + (scaled_body_mass_g*-0.889764) + (scaled_sex*-0.0657631) ); perceptron_layer_1_output_2 = tanh( -0.160659 + (scaled_culmen_length_mm*-0.0955243) + (scaled_culmen_depth_mm*-0.822452) + (scaled_body_mass_g*0.88955) + (scaled_sex*0.0689181) ); probabilistic_layer_combinations_0 = 0.180645 +2.35908*perceptron_layer_1_output_0 +0.497254*perceptron_layer_1_output_1 -0.499956*perceptron_layer_1_output_2 probabilistic_layer_combinations_1 = 0.319912 -0.425221*perceptron_layer_1_output_0 -1.43431*perceptron_layer_1_output_1 +1.43744*perceptron_layer_1_output_2 probabilistic_layer_combinations_2 = -0.505925 -1.93948*perceptron_layer_1_output_0 +0.935236*perceptron_layer_1_output_1 -0.938556*perceptron_layer_1_output_2 sum = exp(probabilistic_layer_combinations_0) + exp(probabilistic_layer_combinations_1) + exp(probabilistic_layer_combinations_2); Adelie = exp(probabilistic_layer_combinations_0)/sum; Gentoo = exp(probabilistic_layer_combinations_1)/sum; Chinstrap = exp(probabilistic_layer_combinations_2)/sum;
References
- Artwork by @allison_horst
- This data is obtained from palmerpenguins package
- Gorman KB, Williams TD, Fraser WR (2014). Ecological sexual dimorphism and environmental variability within a community of Antarctic penguins (genus Pygoscelis). PLoS ONE 9(3):e90081.
- GitHub: Palmerpenguins



