Contents
1. Application type
This example will predict the outcome variable with two values (died within five years or not). Therefore, this is a binary classification project.
The goal here is to model the probability of whether a patient will live for five years or not after being treated with the Levamisole-Fluorouracil combination or chemotherapy.
2. Data set
Data source
The coloncancer.csv file contains the data for this application. The number of instances (rows) in the data set is 607, the number of variables (columns) is 11, and one ID column.
Variables
The number of input variables, or attributes for each sample, is 10. All input variables are binary or numeric-valued. The number of target variables is 1, representing whether the patient survives for 5 years after treatment. The following list summarizes the variables information:
- sex (binary): Male or female.
- age (numeric): The patient’s age at the study’s beginning.
- obstruction (binary): Obstruction of colon by tumor.
- perforation (binary): Perforation of colon.
- adherence (binary): Adherence to nearby organs.
- nodes (numeric): Number of affected lymph nodes.
- more_than_4_nodes (binary): More than 4 positive lymph nodes.
- outcome (binary): Patient died within 5 years or not.
- treatment (binary): Treatment using levamisole and fluorouracil or chemotherapy.
- differ_level (binary, different field for each level): Differentiation of tumor, where level_2 is intermediate forms of tumour with both good and bad prognosis and level_3 is that tumours spread easier than other tumours, and their prognosis is a little worse than for others.
- extent_level (binary, different field for each level): Extent of local spread. 2 = the cancer has grown into the outermost layers of the colon or rectum but has not gone through them. It has not reached nearby organs. It has not spread to nearby lymph nodes or to distant sites. 3 = the cancer has grown through the mucosa into the submucosa. It has spread to 4 to 6 nearby lymph nodes. It has not spread to distant sites. 4 = the cancer may or may not have grown through the wall of the colon or rectum. It might or might not have spread to nearby lymph nodes. It has spread to 1 distant organ (such as the liver or lung) or distant set of lymph nodes, but not to distant parts of the peritoneum (the lining of the abdominal cavity).
Instances
Finally, we set the instances we are going to use. Note that each instance contains a different patient’s input and target variables. The data set is divided into training, validation, and testing subsets. Neural Designer automatically assigns 60% of the instances for training, 20% for generalization, and 20% for testing.
Variables statistics
Then, we can calculate the data statistics and draw a table with the minimums, maximums, means, and standard deviations of all variables in the data set, shown in the next table:
| Minimun | Maximun | Mean | Deviation | |
|---|---|---|---|---|
| sex | 0 | 1 | 0.498 | 0.5 |
| age | 18 | 85 | 59.7 | 12.1 |
| obstruction | 0 | 1 | 0.809 | 0.393 |
| perforation | 0 | 1 | 0.972 | 0.165 |
| adherence | 0 | 1 | 0.858 | 0.349 |
| nodes | 0 | 27 | 3.58 | 3.59 |
| node4 | 0 | 1 | 0.269 | 0.444 |
| treatment | 0 | 1 | 0.491 | 0.5 |
| differ_level | 0 | 1 | 0.715 | 0.452 |
| extent_level | 2 | 4 | 2.94 | 0.401 |
| outcome | 0 | 1 | 0.428 | 0.495 |
Variables distributions
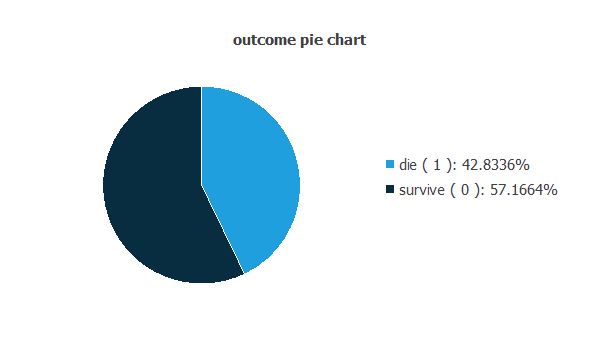
Also, we can calculate the distributions for all variables. The following pie chart shows the distribution for the binary outcome variable. The percentage of samples of the category die (42.8336%) is greater than that of the category survive (57.1664%).
We can also represent the distribution of the treatment variable:
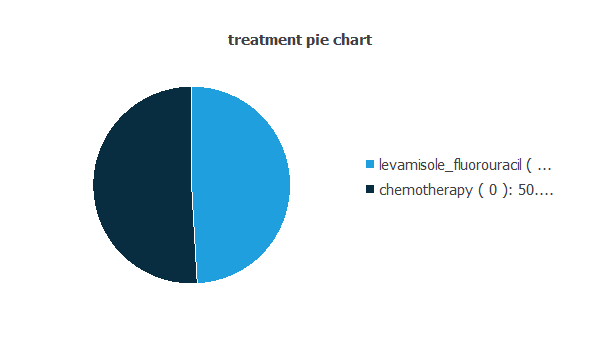
The percentage of samples in the category levamisole_fluorouracil (49.09%) is nearly the same as that in chemotherapy (50.91%).
Inputs-targets correlations
Next, we can calculate the inputs-targets correlations. It might indicate to us what factors most influence the outcome variable:
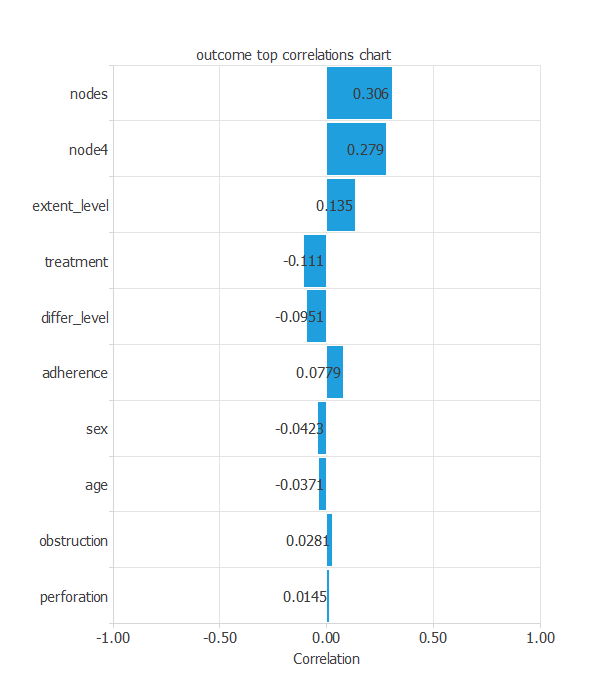
Here, the most correlated variables are nodes, node4, and extent_level.
3. Neural network
The next step is to set up a neural network to represent the classification function. For this type of application, the neural network is composed of:
The scaling layer contains the statistics of the inputs calculated from the data file and the method for scaling the input variables. We select the minimum-maximum method for the binary variables and, for numeric variables, the mean-standard deviation method.
A perceptron layer with a hidden hyperbolic tangent layer is used. The neural network has ten input variables and one target variable, and as our initial choice, we use three neurons.
A probabilistic layer that contains the method for interpreting the outputs as probabilities using a logistic function. As the output layer’s activation function is logistic, the output can already be interpreted as a probability of class membership.
The creation of models for prognostic prediction is a rather complex issue. The resulting model is generally unstable unless the number of patients is vast. Therefore, based on our experience, we have decided to simplify the model. For this purpose, the perceptron layer has been removed to achieve a more stable model by simplifying it. The following figure is a graphical representation of this neural network for colon cancer treatment.
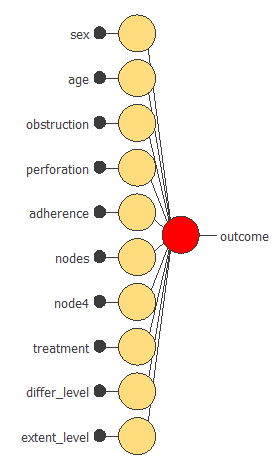
The yellow circles represent scaling neurons, and the red circles are probabilistic neurons. The number of inputs is 10, and the number of outputs is 1.
4. Training strategy
The procedure used to carry out the learning process is called a training strategy. The training strategy is applied to the neural network to obtain the best possible performance. The type of training is determined by how the adjustment of the parameters in the neural network takes place.
We set the weighted squared error with L2 regularization as the loss index.
On the other hand, we use the quasi-Newton method as optimization algorithm.
The following chart shows how errors decrease with the iterations during training. The final training and selection errors are training error = 0.8583 WSE and selection error = 0.8828 WSE, respectively. As in any procedure with randomization of the data, each one of the executions can give slightly different results. The same happens when we switch between the training strategy’s different algorithms and error calculation methods.
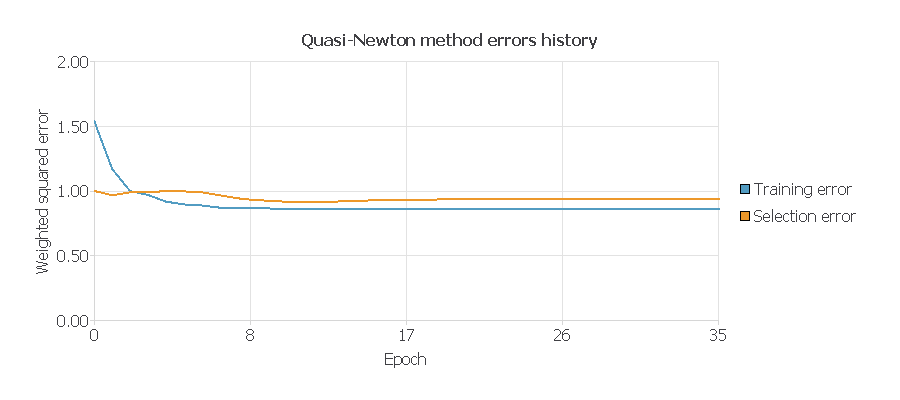
As we can see in the previous image, the behavior of both curves is quite similar. This indicates that our model is stable. We have simplified our model because prognosis applications are quite complex.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties, that is, that which minimizes the error on the selected instances of the data set (the selection error).
Neurons selection. Two frequent problems in designing a neural network are called underfitting and overfitting. The best generalization is achieved using a model with the most appropriate complexity to produce a good data fit.
Inputs selection. Which features should you use to create a predictive model? This difficult question may require in-depth knowledge of the problem domain.
Input selection algorithms automatically extract those features in the data set that provide the best generalization capabilities. They search for the subset of inputs that minimizes the selection error.
6. Testing analysis
The objective of the testing analysis is to validate the generalization performance of the trained neural network. To validate a classification technique, we need to compare the values provided by this technique to the observed values. We can use the ROC curve as it is the standard testing method for binary classification projects.
We obtain a model with a ROC curve of AUC = 0.719, as we can see in the following image:
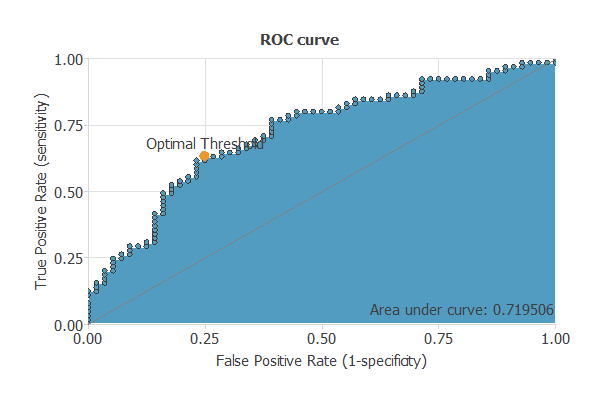
The following table contains the elements of the confusion matrix. This matrix includes the true positives, false positives, false negatives, and true negatives for the variable diagnosis.
| Predicted positive | Predicted negative | |
|---|---|---|
| Real positive | 32(28.9%) | 21(17.4%) |
| Real negative | 19(15.7%) | 46(38.0%) |
The binary classification tests are parameters for measuring the performance of a classification problem with two classes:
- Classification accuracy (ratio of instances correctly classified): 66.9%
- Error rate (ratio of misclassified instances): 33.1%
- Sensitivity (ratio of real positives which are predicted positive): 62.5%
- Specificity (ratio of real negatives which are predicted negative): 70.76%
7. Model deployment
Once we test the neural network’s generalization performance, we can save the neural network for future use in the so-called model deployment mode.
Neural network outputs
We can diagnose new patients by calculating the neural network outputs. For that, we need to know the input variables for them. Here is an example:
- sex: male
- age: 40
- obstruction: no
- perforation: no
- adherence: no
- nodes: 3
- node4: no
- treatment: chemotherapy
- differ_level: level_2
- extent_level: 2
For these inputs, the predicted diagnosis is the following:
- diagnose: there is a 35.68% probability that the patient will die in 5 years.
Response optimization
We can also use Response Optimization. The objective of the response optimization algorithm is to exploit the mathematical model to look for optimal operating conditions.
An example is to minimize the death probability for a female patient.
The next table resumes the conditions for this problem.
| Variable name | Condition | |
|---|---|---|
| Sex | Equal to | 0 |
| Age | None | |
| Obstruction | None | |
| Perforation | None | |
| Adherence | None | |
| Nodes | None | |
| Node4 | None | |
| Treatment | None | |
| Differ level | None | |
| Extent level | None | |
| Diagnose | Minimize |
The next list shows the optimum values for previous conditions.
- sex: female.
- age: 82.73.
- obstruction: no.
- perforation: no.
- adherence: no.
- nodes: 1.
- node4: 0.
- treatment: levamisole and fluorocil.
- differ_level: level_2.
- extent_level: 2.
- diagnose: 7.73% of death probability.
Directional outputs
We can plot directional outputs to study the behavior of the output variable outcome (died within 5 years or not) as the function of single inputs.
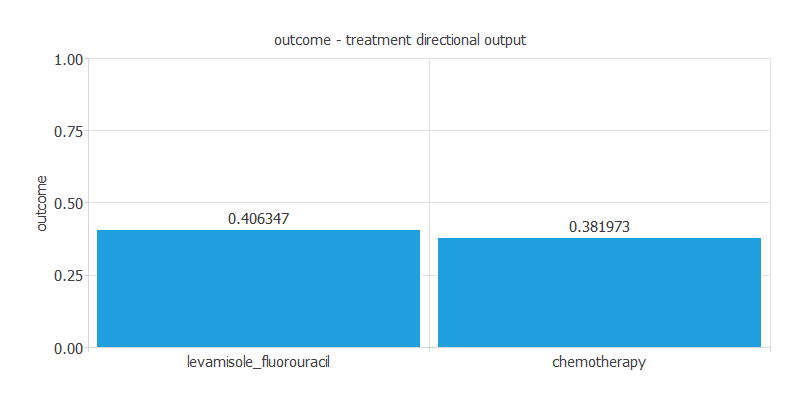
The graph above shows the output outcome as a function of the input treatment. The x and y axes are defined by the range of the variables treatment and outcome, respectively. The patient will have a probability of surviving if the treatment is chemotherapy.
On a descriptive level, the amount of patients that survive is 343. 160 patients use chemotherapy, and 188 use Levamisole and Fluorouracilin. As we can see, there is no huge difference, and the data set does not provide much information. In the tests, the model confirms the trend that chemotherapy has lower survival as an adjuvant treatment.
Mathematical expression
The mathematical expression represented by the neural network is written below. Producing the output outcome takes the inputs sex, age, obstruction, perforation, adherence, nodes, node4, treatment, differ_level, and extent_level. The classification models feed the information through the scaling, perceptron, and probabilistic layers.
scaled_sex = sex*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_age = (age-59.72159958)/12.05169964; scaled_obstruction = obstruction*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_perforation = perforation*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_adherence = adherence*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_nodes = (nodes-3.579900026)/3.593600035; scaled_node4 = node4*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_treatment = treatment*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_differ_level = differ_level*(1+1)/(1-(0))-0*(1+1)/(1-0)-1; scaled_extent_level = (extent_level-2.937289953)/0.3952679932; probabilistic_layer_combinations_0 = 0.267584 -0.0981138*scaled_sex +0.0761505*scaled_age +0.0612563*scaled_obstruction +0.0195698*scaled_perforation -0.278017*scaled_adherence +0.555045*scaled_nodes +0.191396*scaled_node4 -0.254845*scaled_treatment -0.216649*scaled_differ_level +0.248112*scaled_extent_level outcome = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);
The expression above can be exported anywhere, for instance, to a dedicated diagnosis software that the doctor can use.
Conclusions
References
- We have obtained the data for this problem from Coursera.