The central objective is to design a machine learning model that correctly detects gamma rays and discriminates the background.
The Cherenkov gamma telescope uses the atmosphere as a detection medium. It records the image of the Cherenkov radiation produced by an extensive air shower generated by gamma rays.
The Cherenkov photons are collected in patterns (called rain image). These allow us to statistically discriminate those caused by primary gammas (signal) from images of hadronic showers initiated by cosmic rays in the upper atmosphere (background).
The recorded image has the shape of an ellipse. The characteristic parameters of this ellipse (Hillas parameters) are part of the image variables, and we use them for discrimination. We also use, in addition, other discriminating features, such as asymmetric energy deposits along the central axis, the extent of the cluster in the image plane, or the total sum of deposits.
Contents
- Application type.
- Data set.
- Neural network.
- Training strategy.
- Model selection.
- Testing analysis.
- Model deployment.
This example is solved with Neural Designer. To follow it step by step, you can use the free trial.
1. Application type
This is a classification project since the variable to be predicted is binary: gamma (signal) or hadron (background).
2. Data set
The first step is to prepare the data set, which is the source of information for the classification problem. For that, we need to configure the following concepts:
- Data source.
- Variables.
- Instances.
Data source
The data source is the file gamma.csv. It contains the data for this example in comma-separated values (CSV) format. The number of columns is 11, and the number of rows is 19020.
The Corsika simulation program generated the data set: a Monte Carlo code to simulate extensive air showers. In addition, it has been used to simulate the registration of high-energy gamma particles from the Cherenkov gamma telescope using the imaging technique.
Variables
The variables are:
- lenght: Major axis of ellipse (in mm).
- width: Minor axis of the ellipse (in mm).
- size: 0-log of the sum of the content of all pixels (in phot).
- conc: Ratio of the sum of the two highest pixels over size.
- conc1: Ratio of highest pixel over size.
- asym: Distance from highest pixel to center, projected onto major axis (in mm).
- M3Long: Third root of the third moment along the major axis (in mm).
- M3Trans: Third root of the third moment along the minor axis (in mm).
- alpha: Angle of central axis with vector to origin (in degrees).
- distance: Distance from the origin to the ellipse’s center (in mm).
- class: gamma (signal), hadron (background).
Instances
Neural Designer divides the instances randomly into training, selection, and testing subsets. They represent 60% (11412), 20% (3804), and 20% (3804) of the data.
Variables distributions
We can calculate the distributions of all variables. The following figure is the pie chart for the gamma or hadron cases.
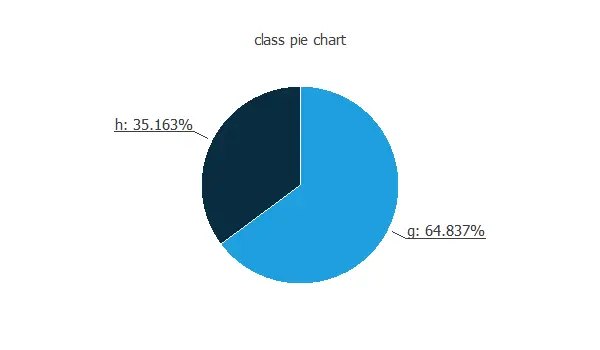
As we can see, most of the samples are gamma signals. The hadron class (background) represents most of the events in the actual data.
Inputs-targets correlations
Finally, the inputs-targets correlations might indicate to us what factors most influence.
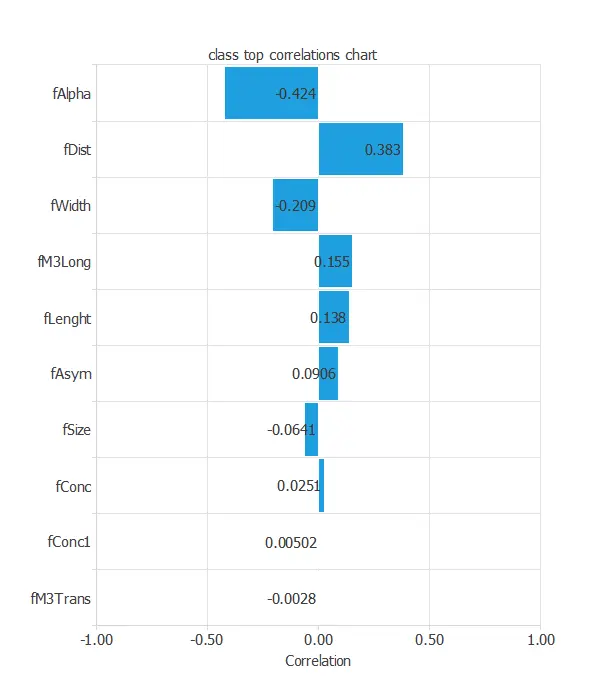
The most correlated variables with the classification are alpha and dist, which refer to ellipse variables. Also, there are not many correlated variables like fConc1 and fM3Trans.
3. Neural network
The second step is to choose a neural network. In classification problems, it is usually composed of:
- A scaling layer.
- Two perceptron layers.
- A probabilistic layer.
The scaling layer contains the statistics on the inputs calculated from the data file and the method for scaling the input variables. Here, the minimum and maximum method has been set. Nevertheless, the mean and standard deviation method would produce very similar results.
The number of perceptron layers is 1. This perceptron layer has 10 inputs and 10 neurons.
Finally, we will set the binary probabilistic method for the probabilistic layer as we want the predicted target variable to be binary.
The following figure is a graphical representation of this classification neural network:
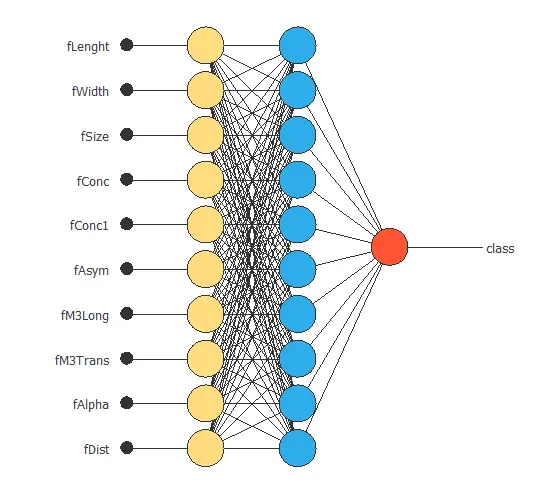
Here, the yellow circles represent scaling neurons, the blue circles represent perceptron neurons, and the red circles represent probabilistic neurons. The number of inputs is 10, and the number of outputs is 1.
4. Training strategy
The fourth step is to set the training strategy, which is composed of:
- Loss index.
- Optimization algorithm.
The loss index chosen for this application is the normalized squared error with L2 regularization.
The error term fits the neural network to the training instances of the data set. The regularization term makes the model more stable and improves generalization.
The optimization algorithm searches for the neural network parameters that minimize the loss index. The quasi-Newton method is chosen here.
The following chart shows how the training and selection errors decrease with the epochs during training.
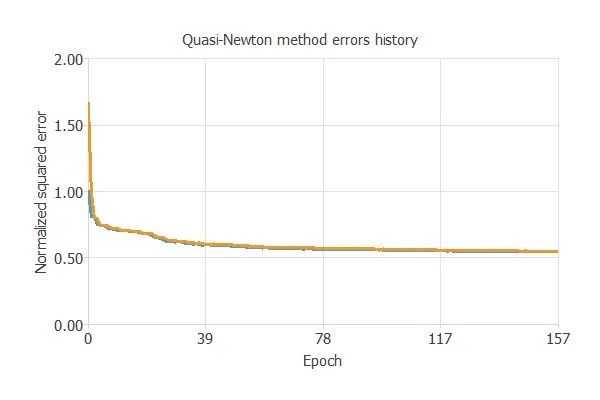
The final values are training error = 0.547 NSE (blue) and selection error = 0.550 NSE (orange).
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties, which minimizes the error on the selected instances of the data set.
More specifically, we want to find a neural network with a selection error of less than 0.550 WSE, which is the value we have achieved.
Order selection algorithms train several network architectures with a different number of neurons and select that with the smallest selection error.
The incremental order method starts with a few neurons and increases the complexity at each iteration.
6. Testing analysis
The last step is to test the generalization performance of the trained neural network.
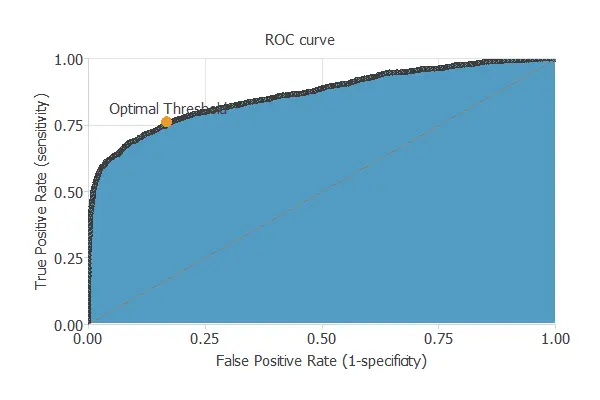
The objective of the testing analysis is to validate the generalization performance of the trained neural network. To validate a classification technique, we need to compare the values provided by this technique to the observed values. We can use the ROC curve as it is the standard testing method for binary classification projects.
In the confusion matrix, the rows represent the targets (or real values), and the columns represent the corresponding outputs (or predictive values).
The diagonal cells show the correctly classified cases, and the off-diagonal cells show the misclassified instances.
| Predicted positive (gamma) | Predicted negative (background) | |
|---|---|---|
| Real positive (gamma) | 2120 (55.8%) | 283 (7.4%) |
| Real negative (background) | 407 (10.7%) | 993 (26.1%) |
As we can see, the number of instances the model can correctly predict is 3114 (81.9%), while it misclassifies 690 (18.1%).
This shows that our predictive model has a great classification accuracy.
The next list depicts the binary classification tests for this application:
- Classification accuracy: 81.9% (percentage of correctly classified samples).
- Error rate: 18.1% (percentage of misclassified samples).
- Sensitivity: 88.2% (percentage of actual positive classified as positive).
- Specificity: 70.9% (percentage of actual negative classified as negative).
7. Model deployment
The neural network is now ready to predict outputs for inputs it has never seen. This process is called model deployment.
We calculate the neural network outputs from the different variables to classify a given signal. For instance:
- lenght: 341.4 mm.
- width: 190.3 mm.
- size: 25.7 phot.
- conc: 0.4.
- conc1: 0.2.
- asym: 24.4 mm.
- M3Long: 118.4 mm.
- M3Trans: 1.5 mm.
- alpha: 182.6 degrees.
- dist: 225.2 mm.
- Probability of signal gamma: 80%.
The neural network would classify the signal as a gamma-ray signal for this case.
The objective of the Response Optimization algorithm is to exploit the mathematical model to look for optimal operating conditions. Indeed, the predictive model allows us to simulate different operating scenarios and adjust the control variables to improve efficiency.
An example is to maximize signal gamma probability while maintaining the focal length below the desired value.
The following table resumes the conditions for this problem.
| Variable name | Condition | |
|---|---|---|
| fLength | Less than | 50 |
| fWidth | None | |
| fSize | None | |
| fConc | None | |
| fConc1 | None | |
| fAsym | None | |
| fM3Long | None | |
| fM3Trans | None | |
| fAlpha | None | |
| fDist | None | |
| Probability of signal gamma | Maximize |
The following list shows the optimum values for previous conditions.
- fLenght: 36.3773 mm.
- fWidth: 602.126 mm.
- fSize: 22.286 phot.
- fConc: 0.865986.
- fConc1: 0.0815936.
- fAsym: -269.233 mm.
- fM3Long: -823.624 mm.
- fM3Trans: -215.942 mm.
- fAlpha: 35.5603 degrees.
- fDist: 13.9842 mm.
- Probability of signal gamma: 80%.
The mathematical expression of the trained neural network is listed below.
scaled_fLenght = fLenght*(1+1)/(999.9559937-(1))-1*(1+1)/(999.9559937-1)-1;
scaled_fWidth = fWidth*(1+1)/(998.8590088-(0))-0*(1+1)/(998.8590088-0)-1;
scaled_fSize = fSize*(1+1)/(53.23300171-(2.038000107))-2.038000107*(1+1)/(53.23300171-2.038000107)-1;
scaled_fConc = fConc*(1+1)/(0.8930000067-(0.0131000001))-0.0131000001*(1+1)/(0.8930000067-0.0131000001)-1;
scaled_fConc1 = fConc1*(1+1)/(0.6751999855-(0.0003000000142))-0.0003000000142*(1+1)/(0.6751999855-0.0003000000142)-1;
scaled_fAsym = fAsym*(1+1)/(999.0479736-(-999.1749878))+999.1749878*(1+1)/(999.0479736+999.1749878)-1;
scaled_fM3Long = fM3Long*(1+1)/(998.901001-(-999.8439941))+999.8439941*(1+1)/(998.901001+999.8439941)-1;
scaled_fM3Trans = fM3Trans*(1+1)/(999.0230103-(-995.164978))+995.164978*(1+1)/(999.0230103+995.164978)-1;
scaled_fAlpha = fAlpha*(1+1)/(899.7979736-(0))-0*(1+1)/(899.7979736-0)-1;
scaled_fDist = fDist*(1+1)/(999.7470093-(1))-1*(1+1)/(999.7470093-1)-1;
perceptron_layer_0_output_0 = logistic[ 0.692146 + (scaled_fLenght*0.467332)+ (scaled_fWidth*-0.450438)+ (scaled_fSize*0.682765)+ (scaled_fConc*-1.3431)+ (scaled_fConc1*-0.572128)+ (scaled_fAsym*0.0648873)+ (scaled_fM3Long*0.599988)+ (scaled_fM3Trans*0.208405)+ (scaled_fAlpha*-1.42559)+ (scaled_fDist*-0.606827) ];
perceptron_layer_0_output_1 = logistic[ 0.0627224 + (scaled_fLenght*0.326231)+ (scaled_fWidth*0.000709985)+ (scaled_fSize*-0.21026)+ (scaled_fConc*0.304741)+ (scaled_fConc1*-0.0130853)+ (scaled_fAsym*0.0342383)+ (scaled_fM3Long*0.0329861)+ (scaled_fM3Trans*-0.0452345)+ (scaled_fAlpha*-0.335708)+ (scaled_fDist*0.116437) ];
perceptron_layer_0_output_2 = logistic[ 1.49828 + (scaled_fLenght*-0.919557)+ (scaled_fWidth*-0.410504)+ (scaled_fSize*-0.0886092)+ (scaled_fConc*0.718132)+ (scaled_fConc1*0.306611)+ (scaled_fAsym*-0.0987389)+ (scaled_fM3Long*-0.237907)+ (scaled_fM3Trans*-0.148078)+ (scaled_fAlpha*1.84953)+ (scaled_fDist*-0.552449) ];
perceptron_layer_0_output_3 = logistic[ 4.59582 + (scaled_fLenght*-0.244476)+ (scaled_fWidth*-0.864021)+ (scaled_fSize*-0.120483)+ (scaled_fConc*0.536859)+ (scaled_fConc1*-0.740612)+ (scaled_fAsym*0.200571)+ (scaled_fM3Long*-0.114687)+ (scaled_fM3Trans*0.210845)+ (scaled_fAlpha*-0.120278)+ (scaled_fDist*5.90061) ];
perceptron_layer_0_output_4 = logistic[ 0.0401848 + (scaled_fLenght*-0.491856)+ (scaled_fWidth*-0.180537)+ (scaled_fSize*0.205085)+ (scaled_fConc*-0.123382)+ (scaled_fConc1*0.155739)+ (scaled_fAsym*-0.0233865)+ (scaled_fM3Long*-0.0112962)+ (scaled_fM3Trans*0.024652)+ (scaled_fAlpha*0.573812)+ (scaled_fDist*-0.34138) ];
perceptron_layer_0_output_5 = logistic[ 0.0323723 + (scaled_fLenght*0.130772)+ (scaled_fWidth*-3.67782)+ (scaled_fSize*0.63322)+ (scaled_fConc*0.556959)+ (scaled_fConc1*0.133669)+ (scaled_fAsym*0.850306)+ (scaled_fM3Long*1.81974)+ (scaled_fM3Trans*0.262492)+ (scaled_fAlpha*-0.14081)+ (scaled_fDist*-0.40068) ];
perceptron_layer_0_output_6 = logistic[ -0.0059346 + (scaled_fLenght*-0.473911)+ (scaled_fWidth*-0.137564)+ (scaled_fSize*0.215851)+ (scaled_fConc*-0.149254)+ (scaled_fConc1*0.143802)+ (scaled_fAsym*-0.00899171)+ (scaled_fM3Long*-0.01149)+ (scaled_fM3Trans*0.0439353)+ (scaled_fAlpha*0.543843)+ (scaled_fDist*-0.331678) ];
perceptron_layer_0_output_7 = logistic[ 0.00128206 + (scaled_fLenght*-0.434998)+ (scaled_fWidth*-0.103269)+ (scaled_fSize*0.186503)+ (scaled_fConc*-0.159589)+ (scaled_fConc1*0.100581)+ (scaled_fAsym*-0.0227729)+ (scaled_fM3Long*0.00090008)+ (scaled_fM3Trans*0.029425)+ (scaled_fAlpha*0.432715)+ (scaled_fDist*-0.241261) ];
perceptron_layer_0_output_8 = logistic[ -0.501099 + (scaled_fLenght*3.05783)+ (scaled_fWidth*-1.3152)+ (scaled_fSize*0.162658)+ (scaled_fConc*1.18554)+ (scaled_fConc1*1.37125)+ (scaled_fAsym*0.38648)+ (scaled_fM3Long*0.445544)+ (scaled_fM3Trans*0.551555)+ (scaled_fAlpha*0.268025)+ (scaled_fDist*-0.130231) ];
perceptron_layer_0_output_9 = logistic[ 0.973201 + (scaled_fLenght*-0.934547)+ (scaled_fWidth*0.362176)+ (scaled_fSize*0.17335)+ (scaled_fConc*-1.14552)+ (scaled_fConc1*-0.330626)+ (scaled_fAsym*-0.070589)+ (scaled_fM3Long*-0.203409)+ (scaled_fM3Trans*0.168493)+ (scaled_fAlpha*1.08351)+ (scaled_fDist*3.32507) ];
probabilistic_layer_combinations_0 = -0.376285 -2.51424*perceptron_layer_0_output_0 +0.37477*perceptron_layer_0_output_1 -2.88237*perceptron_layer_0_output_2 +5.95298*perceptron_layer_0_output_3 -1.054*perceptron_layer_0_output_4 +3.7831*perceptron_layer_0_output_5 -1.02447*perceptron_layer_0_output_6 -0.864628*perceptron_layer_0_output_7 -3.07973*perceptron_layer_0_output_8 -3.22218*perceptron_layer_0_output_9
class = 1.0/(1.0 + exp(-probabilistic_layer_combinations_0);
logistic(x){
return 1/(1+exp(-x))
}
We have just built a predictive model to determine if the measured data come from gamma rays or from the hadron shower that we have considered as background.
References
- The data for this problem has been taken from the UCI Machine Learning Repository.
- Bock, R.K., Chilingarian, A., Gaug, M., Hakl, F., Hengstebeck, T., Jirina, M., Klaschka, J., Kotrc, E., Savicky, P., Towers, S., Vaicilius, A., Wittek W. (2004). Methods for multidimensional event classification: a case study using images from a Cherenkov gamma-ray telescope. Nucl.Instr.Meth. A, 516, pp. 511-528.
- P. Savicky, E. Kotrc. Experimental Study of Leaf Confidences for Random Forest. Proceedings of COMPSTAT 2004, In: Computational Statistics. (Ed.: Antoch J.) – Heidelberg, Physica Verlag 2004, pp. 1767-1774.
- J. Dvorak, P. Savicky. Softening Splits in Decision Trees Using Simulated Annealing. Proceedings of ICANNGA 2007, Warsaw, (Ed.: Beliczynski et. al), Part I, LNCS 4431, pp. 721-729.


