For this study, we use machine learning to model superconductors’ critical temperature from an extensive data set of the chemical properties of 21263 superconductors.
Superconductivity has been the focus of enormous research efforts since its discovery more than a century ago.
Yet, some features of this unique phenomenon remain poorly understood.
The prime among these is the connection between the chemical/structural properties of materials and the phenomenon of superconductivity.
Knowing a superconductor’s critical temperature is crucial because the material exhibits zero electrical resistance at that temperature.
Contents
1. Application type
This is an approximation project since the variable to be predicted is continuous (Critical Temperature).
This study uses a data-driven approach to create a statistical model that predicts Tc based on its chemical formula.
2. Data set
The first step is to prepare the data set, which is the source of information for the approximation problem. It is composed of:
- Data source.
- Variables.
- Instances.
The file superconductor.csv contains the data for this example. Here, the number of variables (columns) is 82, and the number of instances (rows) is 21263.
Variables
In that way, this problem has the following variables:
Atomic Properties
- Atomic mass: Total rest mass of protons and neutrons, measured in atomic mass units (AMU).
- Atomic radius: Estimated size of the atom, measured in picometers (pm).
- Valence: Typical number of chemical bonds an element forms (unitless).
Electronic Properties
- First ionization energy: Energy needed to remove a valence electron, in kJ/mol.
- Electron affinity: Energy change when an electron is added to a neutral atom, in kJ/mol.
Physical Properties
- Density: Mass per unit volume at standard temperature and pressure, in kg/m³.
- Fusion heat: Energy required for a solid-to-liquid phase change at constant temperature, in kJ/mol.
- Thermal conductivity: Ability of a material to conduct heat, in W/(m·K).
Target Variable
Critical temperature: Temperature below which the material becomes superconducting, measured in Kelvin (K).
The ratios of the elements in the material are used to define features:
$$p_{i}=frac{j}{sum_{i=1}^{n} j}$$
Where ( j ) is the proportion of an element in the compound.
The fractions of total thermal conductivities are used as well:
$$w_{i}=frac{t_{i}}{sum_{i=1}^{n} t_{i}}$$
Where ( t_{i} ) are the thermal conductivity coefficients.
We will also need intermediate values for calculating features:
$$A_{i}=frac{p_{i}w_{i}}{sum_{i=1}^{n} p_{i}w_{i}}$$
The following table summarizes the procedure for feature extraction from the material’s chemical formula.
| Feature & description | Formula |
|---|---|
| Mean | $$mu=sum_{i=1}^{n} frac{t_{i}}{i}$$ |
| Weighted mean | $$nu=sum_{i=1}^{n} p_{i} t_{i}$$ |
| Geometric mean | $$sqrt{sum_{i=1}^{n} t_{i}}$$ |
| Weighted geometric mean | $$sum_{i=1}^{n} t_{i}^{p_{i}}$$ |
| Entropy | $$-sum_{i=1}^{n} w_{i} ln w_{i}$$ |
| Weighted entropy | $$-sum_{i=1}^{n} A_{i} ln A_{i}$$ |
| Range | $$t_{(max)} – t_{(min)}$$ |
| Weighted range | $$p(t_{(max)})t_{(max)} – p(t_{(min)})t_{(min)}$$ |
| Standard deviation | $$left[frac{1}{2}left(sum_{i=1}^{n} (t_{i}-mu)^{2}right)right]^{frac{1}{2}}$$ |
| Weighted standard deviation | $$left[sum_{i=1}^{n} p_{i}(t_{i}-nu)^{2}right]^{frac{1}{2}}$$ |
For instance, for the chemical compound Re7Zr1 with these Rhenium and Zirconium’s thermal conductivity coefficients: ( t_{1} = 48,,W/(mK) ) and ( t_{2} = 23,,W/(mK) ), respectively.
We can calculate features like the weighted geometric mean and obtain a value of ( 43.21 )
They are divided randomly into training, selection, and testing subsets, containing 60%, 20%, and 20% of the instances, respectively. More specifically, 12759 samples are used here for training, 4252 for validation, and 4252 for testing.
Once all the data set information has been established, we will perform some analytics to check the quality of the data.
Data distribution
For instance, we can calculate the data distribution. The following figure depicts the histogram for the target variable.
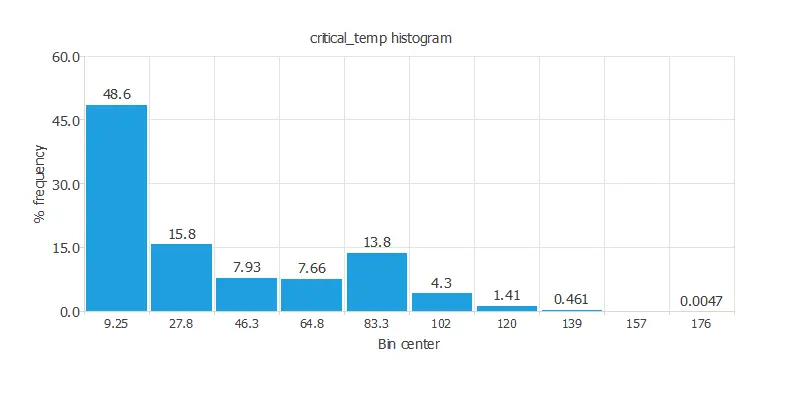
The above graph shows more chemical compounds with low critical temperatures.
This could be explained by the fact that finding a superconductor with a relatively high critical temperature is difficult.
To find superconductor properties, such as current conductivity with zero resistance, we must reduce the material temperature a lot.
Inputs-targets correlations
The following figure depicts input-target correlations. This might help us see the input’s influence on the critical temperature.
With so many input variables, the chart shows the top 20.
We can also plot a scatter chart with the critical temperature versus the weighted mean valence.
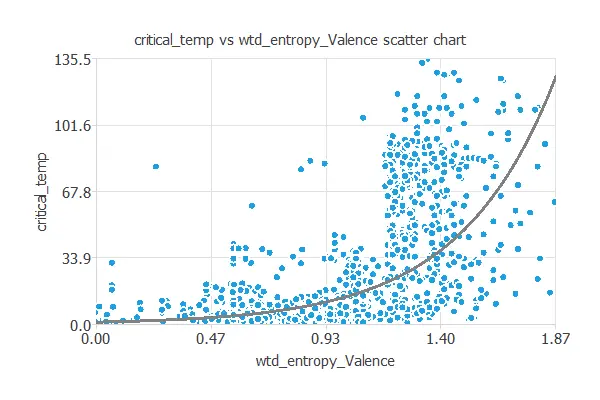
As we can see, the critical temperature decreases when we increase the weighted mean valence logarithmically.
3. Neural network
The neural network will output the critical temperature as a function of different chemical properties.
For this approximation example, the neural network is composed of:
- Scaling layer.
- Perceptron layers.
- Unscaling layer.
Scaling layer
The scaling layer transforms the original inputs to normalized values. Here, the Minimum-Maximum deviation scaling method is set so that the input values have a minimum of -1 and a maximum of +1.
Dense layers
Here, two perceptron layers are added to the neural network. This number of layers is enough for most applications. The first layer comprises 81 inputs and 3 neurons, while the second layer consists of 3 inputs and 1 neuron.
Unscaling layer
The unscaling layer transforms the normalized values from the neural network into the original outputs. Here, the Minimum-Maximum deviation scaling method and the mean and standard deviation unscaling method will also be used.
Neural network graph
The figure below shows the final architecture for the neural network.
4. Training strategy
The next step is to select an appropriate training strategy that defines what the neural network will learn.
A general training strategy consists of two concepts:
- A loss index.
- An optimization algorithm.
Loss index
The loss index chosen is the normalized squared error with L2 regularization. This loss index is the default in approximation applications.
Optimization algorithm
The optimization algorithm that we chose is the quasi-Newton method.
This optimization algorithm is the default for medium-sized applications like this one.
Training
Once we have established the strategy, we can train the neural network. The following chart shows how the training (blue) and selection (orange) errors decrease with the training epoch during the training process.
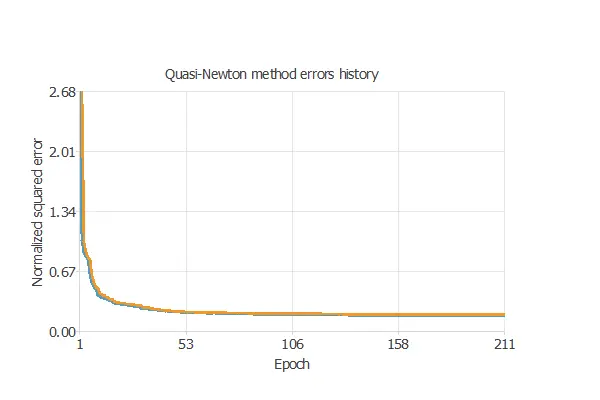
The key training result is the final selection error, which reflects the neural network’s ability to generalize.
5. Model selection
The objective of model selection is to find the network architecture with the best generalization properties.
Thus, we aim to reduce the final selection error obtained previously (0.178 NSE).
The model achieves the best selection error when its complexity is appropriate for achieving a good fit to the data. Order selection algorithms are responsible for finding the optimal number of perceptrons in the neural network.
Notably, the final selection error takes a minimum value at some point. Here, the optimal number of neurons is 10, corresponding to a 0.164 selection error.
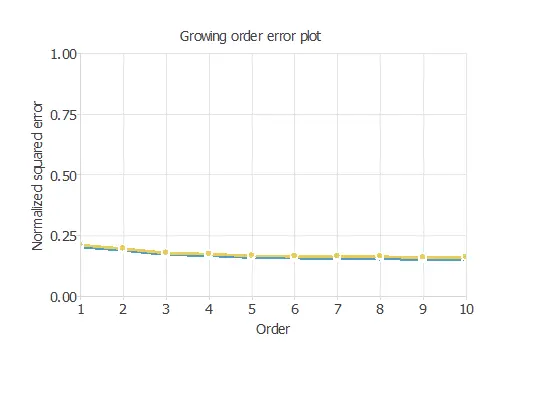
The above chart shows the error history for the different subsets during the selection of growing neurons. The blue line represents the training error, and the yellow line symbolizes the selection error.
6. Testing analysis
The goal of testing is to assess the network’s generalization by comparing its predicted values with the observed ones.
Goodnes-of-fit
A standard testing technique in approximation problems is to perform a linear regression analysis between the predicted and the real values using an independent testing set.
The following figure illustrates a graphical output provided by this testing analysis.
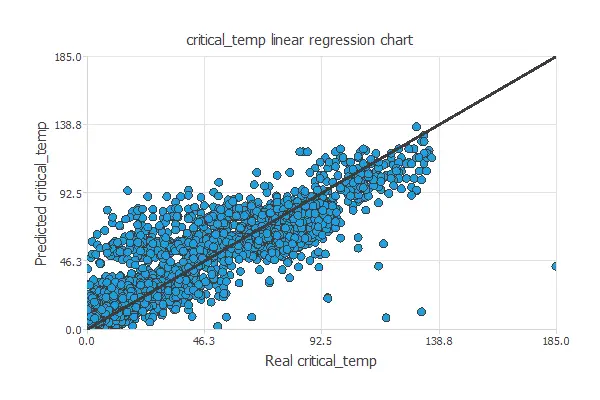
From the above chart, we can see that the neural network is predicting well the entire range of the critical temperature data.
The correlation value is R2 = 0.911, which is close to 1.
7. Model deployment
The model is now ready to estimate the critical temperature of a specific chemical compound.
Directional output
We can plot a neural network’s directional output to see how the emissions vary with a given input for all other fixed inputs. The following plot shows the critical temperature as a function of the geometric mean valence through the following point:
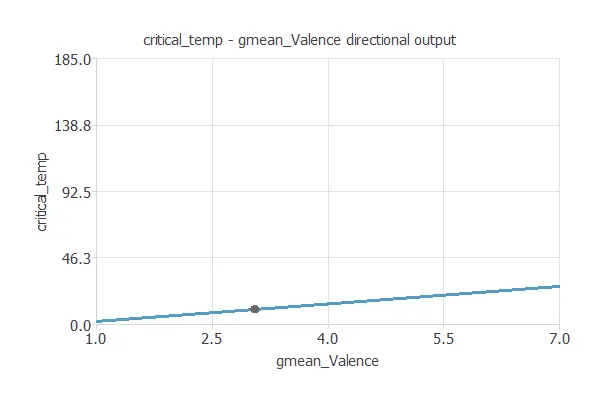
For this study, it is important to mention other valuable tasks of the Model Deployment Tool we refer to: Calculate Outputs.
Additionally, we could think about creating a semiconductor with specific chemical quantities. With this tool, we can select the inputs and calculate the optimal superconductor critical temperature for our desired purpose.
The superconductor.py contains the Python code to calculate a compound critical temperature.
Conclusions
In this post, we build a machine learning model to estimate the superconducting critical temperature as a function of the features extracted from the superconductor’s chemical formula.
Specifically, these features include atomic radius, valence, electron affinity, atomic mass, etc.
References
- UCI Machine Learning Repository. Superconductivity Data Set.
